02TheTensorFlowWay（2）

Implementing Loss Functions：

        损失函数是非常重要的机器学习算法。他们测量模型输出和目标（真理）值之间的距离。

        Getting ready：

        为了优化我们的机器学习算法，我们将需要评估的结果。结果tensorflow评价取决于指定损失函数。损失函数告诉TensorFlow如何好或坏的预测进行了比较理想的结果。在大多数情况下，我们将有一组数据和一个目标来训练我们的算法。损失函数比较目标的预测，并给出了两者之间的数值距离。

        如下，我们将覆盖主要的损失函数，我们可以实现在TensorFlow。

        为了了解不同的损失函数如何操作，我们将在这个配方中绘制它们。我们将rststart计算图和负载matplotlib，Python绘图库，如下：

import matplotlib.pyplot as plt

import tensorflow as tf

        How to do it...：

        首先，我们将讨论损失函数的回归，即，预测连续因变量。首先，我们将创建一个序列，我们的预测和目标作为一个张量。我们将结果输出在500 x 1和1之间。见下一节的输出图。使用以下代码：

x_vals = tf.linspace(-1., 1., 500)

target = tf.constant(0.)

        1. L2 loss损失也称为欧氏损失函数。它只是距离目标的距离的平方。在这里，如果目标是零，我们将计算的损失函数。L2范数是一个伟大的损失函数，因为它是非常弯曲的目标附近，算法可以使用这个事实收敛到目标更慢，越接近，得到如下：

l2_y_vals = tf.square(target - x_vals)

l2_y_out = sess.run(l2_y_vals)
        ** TensorFlow有一个内置的L2范数，称为nn.l2_loss()。这个函数实际上是一半以上的L2范数。换句话说，它和以前一样，但除以2。

        2.L1 loss也称为绝对损失函数。我们没有取差额，而是取绝对值。L1范数是更好的离群值比L2范数，因为它不是陡峭的较大值。要注意的一个问题是在目标的L1范数是不光滑的，这可能会导致算法不收敛良好。如下所示：

l1_y_vals = tf.abs(target - x_vals)

l1_y_out = sess.run(l1_y_vals)

        3.Pseudo Huber loss是一个连续光滑逼近的胡贝尔损失函数。这种损失函数试图采取最好的L1和L2规范的凸附近的目标和陡峭的极端值。该窗体依赖于一个额外的参数，delta，它决定了它将是多么陡峭。我们将图两种形式，Delta1 = 0.25和Delta2 = 5以示区别，如下：

delta1 = 0.25 and delta2 = 5 to show the difference, as follows:

delta1 = tf.constant(0.25)

phuber1_y_vals = tf.mul(tf.square(delta1), tf.sqrt(1. + tf.square((target - x_vals)/delta1)) - 1.)

phuber1_y_out = sess.run(phuber1_y_vals)

delta2 = tf.constant(5.)

phuber2_y_vals = tf.mul(tf.square(delta2), tf.sqrt(1. + tf.square((target - x_vals)/delta2)) - 1.)

phuber2_y_out = sess.run(phuber2_y_vals)

        4.分类的损失函数来评估损失预测分类结果。
        5.我们需要设定我们的预测（x_vals）和target。我们将保存输出并在下一节中绘制它们。使用以下：

x_vals = tf.linspace(-3., 5., 500)

target = tf.constant(1.)

targets = tf.fill([500,], 1.)

        6.Hinge loss主要用于支持向量机，但也可以用于神经网络。它的目的是计算两个目标类之间的损失，1和- 1。在下面的代码中，我们使用目标值1，这样越接近我们的预测接近到1，损失值越低：

hinge_y_vals = tf.maximum(0., 1. - tf.mul(target, x_vals))

hinge_y_out = sess.run(hinge_y_vals)

        7.Cross-entropy loss的二进制的情况下，有时也被称为逻辑损失函数。它来时，我们预测这两个班0或1。我们希望测量实际类（0或1）到预测值之间的距离，这个值通常是在0到1之间的实数。为了测量这个距离，我们可以使用交叉熵公式从信息理论，如下：

xentropy_y_vals = - tf.mul(target, tf.log(x_vals)) - tf.mul((1. - target), tf.log(1. - x_vals))

xentropy_y_out = sess.run(xentropy_y_vals)
        8. Sigmoid cross entropy loss是以前的损失函数非常相似，除了将x的Sigmoid函数之前，我们把他们的交叉熵损失，如下：

xentropy_sigmoid_y_vals = tf.nn.sigmoid_cross_entropy_with_logits(x_vals, targets)

xentropy_sigmoid_y_out = sess.run(xentropy_sigmoid_y_vals)
         9.Weighted cross entropy loss是一个加权版本的 sigmoid cross entropy loss。我们提供了一个权重的积极目标。举个例子，我们将0.5的正目标加权如下：

weight = tf.constant(0.5)

xentropy_weighted_y_vals = tf.nn.weighted_cross_entropy_with_logits(x_vals, targets, weight)

xentropy_weighted_y_out = sess.run(xentropy_weighted_y_vals)

        10.Softmax cross-entropy loss在非归一化输出。这个函数是用来测量损失时，只有一个目标类别，而不是多个。因此，功能转换的输出通过softmax函数的概率分布，然后计算损失函数从一个真实的概率分布，如下：

unscaled_logits = tf.constant([[1., -3., 10.]])

target_dist = tf.constant([[0.1, 0.02, 0.88]])

softmax_xentropy = tf.nn.softmax_cross_entropy_with_logits(unscaled_logits, target_dist)

print(sess.run(softmax_xentropy))

       [ 1.16012561]
        11.Sparse softmax cross-entropy loss是以前一样，只不过是一个概率分布的目标，它是一个指数的范畴是真实的。而不是一个稀疏的全零目标向量的一个值，我们只是传递的指数，其中类别是真正的价值，如下：

unscaled_logits = tf.constant([[1., -3., 10.]])

sparse_target_dist = tf.constant([2])

sparse_xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(unscaled_logits, sparse_target_dist)

print(sess.run(sparse_xentropy))

        [ 0.00012564]

        How it works...：
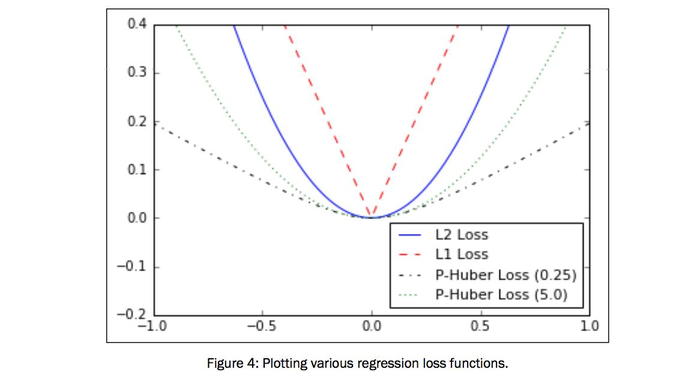
        这里介绍的是如何用Matplotlib绘制回归的损失函数：
x_array = sess.run(x_vals)

plt.plot(x_array, l2_y_out, 'b-', label='L2 Loss')

plt.plot(x_array, l1_y_out, 'r--', label='L1 Loss')

plt.plot(x_array, phuber1_y_out, 'k-.', label='P-Huber Loss (0.25)')

plt.plot(x_array, phuber2_y_out, 'g:', label='P'-Huber Loss (5.0)')

plt.ylim(-0.2, 0.4)

plt.legend(loc='lower right', prop={'size': 11})

plt.show()

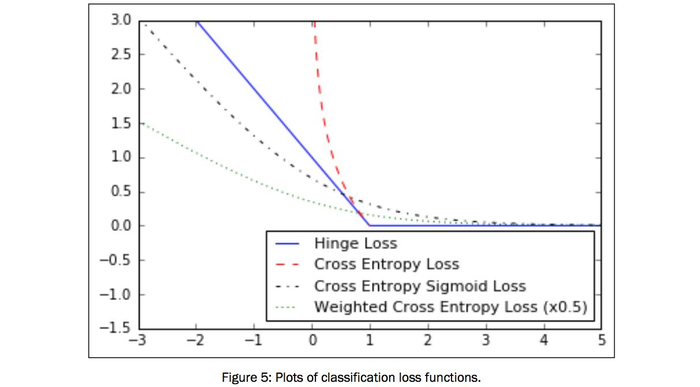
        这里是如何使用Matplotlib绘制各种分类损失函数：

x_array = sess.run(x_vals)

plt.plot(x_array, hinge_y_out, 'b-', label='Hinge Loss')

plt.plot(x_array, xentropy_y_out, 'r--', label='Cross Entropy Loss')

plt.plot(x_array, xentropy_sigmoid_y_out, 'k-.', label='Cross Entropy Sigmoid Loss')

plt.plot(x_array, xentropy_weighted_y_out, g:', label='Weighted Cross Enropy Loss (x0.5)')

plt.ylim(-1.5, 3)

plt.legend(loc='lower right', prop={'size': 11})

plt.show()

        There's more...：

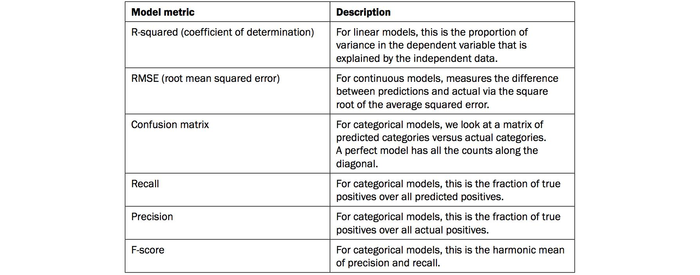
        这里是一个表总结了不同的损失函数：

        在评估一个模型时还有许多其他的指标要看。以下是一些需要考虑的列表：