其实就是Matlab教学视频的理解
视频地址
https://www.mathworks.com/videos/series/understanding-kalman-filters.html
知乎大神的解释
https://zhuanlan.zhihu.com/p/129370341
https://zhuanlan.zhihu.com/p/129694693
wiki
https://en.wikipedia.org/wiki/Kalman_filter
你碰到一个人,给你的帅气打十分,你自己给自己打八分,那你实际有多帅呢?你不断地碰到更多的人,怎么用这些数据估计自己最真实客观的颜值呢?Kalman Filters可以神奇地帮你去除那些噪声
简介
在统计和控制理论中,卡尔曼滤波(也称为线性二次估计(LQE))是一种算法,该算法使用随时间推移观察到的一系列测量值(包含统计噪声和其他误差),并生成未知变量的估计,而这些估计往往会通过估计每个时间范围内变量的联合概率分布,比仅基于单个测量的结果更准确
通俗解释
1 房间温度
你在一个房间,可以通过温度计和自己的感觉获得两个温度(包含噪声),然后根据这两个温度你给出一个实际温度的猜测温度,随着时间的推移,你不断地重复这个操作,你怎么让猜测的温度更接近实际温度,更可靠准确。直接取两个温度的平均值吗?
2 火箭尾焰温度
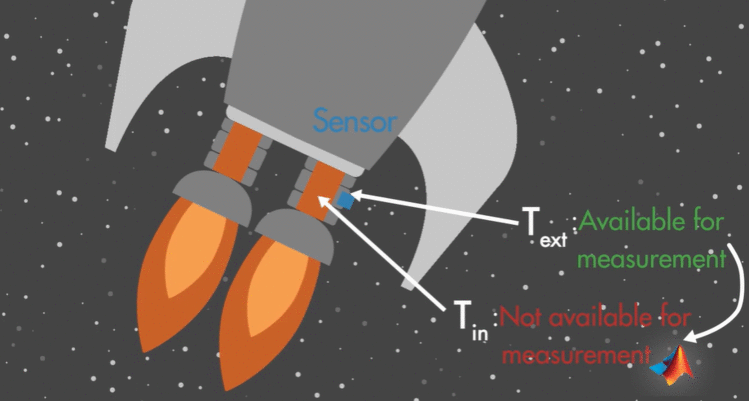
火箭的尾焰温度很高,不能直接测量,需要把传感器放在紧靠尾焰,温度较低的外部。
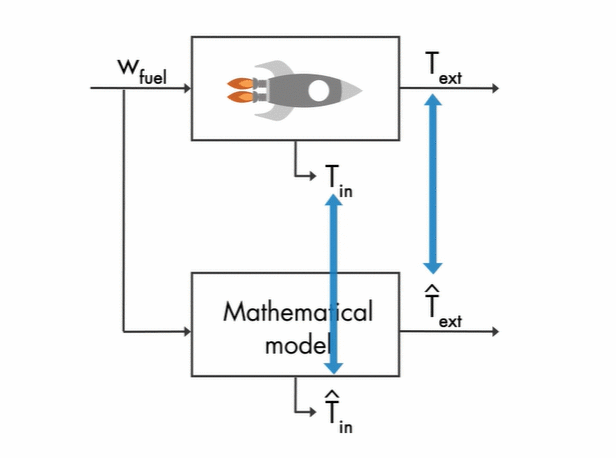
通过一个温度传导公式,你可以通过外部温度获得尾焰温度,你也可以根据以前加入的所有燃料,通过火箭模型,计算出外部温度,尾焰温度,燃料在不断地添加的过程中,你怎么通过测量获得估计和火箭模型获得的估计,估计真实的尾焰温度。注意这是一个过程,你在不断地给出估计值,你要做的是,让你的估计不要偏离实际温度,并且尽可能越来越接近真实值,即使被外星人攻击了,短暂地偏离了,也能快速地拉回来
3 自动驾驶
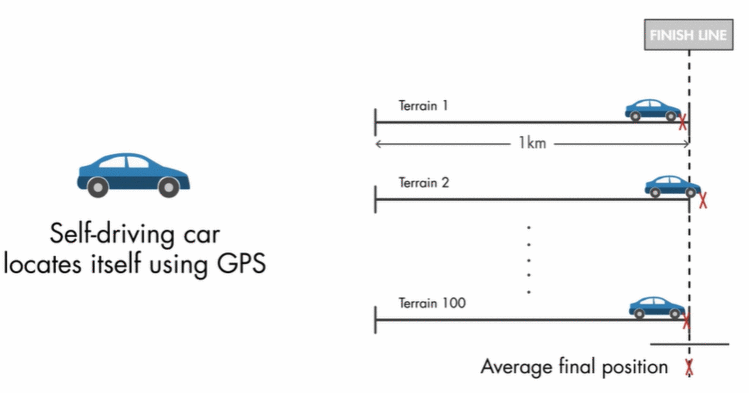
你很缺钱,参加一个自动驾驶比赛,比赛规定每辆车跑1km,测试100次,谁的车停的离终点线最近,谁就赢得100万。要想赢,这一百次你的平均距离要接近1km(均值接近1km),并且每次都尽可能接近1km(方差小)。

你很牛,知道了每个加速减速的操作以后,车子不用跑,用一个模型就计算出了每个时间的位置,速度,你还能通过GPS实时获取车子的位置,然后你有了两个位置,怎么通过这两个位置估计车子实际跑时候的位置,并且使得这个估计越来越准?
为什么这个问题可以有解
虽然测量估计和实际环境都有噪声,但这个噪声一般来说都是服从高斯分布或者其他分布的。测量估计和模型估计的可信度可以通过大量实验增加其可靠度,即使你刚开始的猜测不靠谱,这个算法也可以像梯度下降那样,让你很快变得可靠
State Estimator(状态估计器)
火箭尾焰温度的估计可以用下图的状态估计器描述。T^in\hat{T}_{in}T^in、T^ext\hat{T}_{ext}T^ext是模型预测的内部温度。通过K将模型预测值T^ext\hat{T}_{ext}T^ext和测量值Text{T}_{ext}Text联系起来,将他们的差反馈给模型,用于改进预测可靠度。

- xxx:当前状态(k时刻实际内部温度)
- yyy:测量状态(k时刻测量外部温度)
- uuu:控制向量(k时刻添加燃料量)
- AAA:状态转移模型(k时刻状态转向k+1时刻)
- BBB:输入控制模型(输入对状态转移的作用)
- CCC:观测模型(真实值转向观察值)
- KKK:Kalman 增益
- x˙\dot{x}x˙:当前状态的一阶导数,也就是当前状态的变化趋势,有时这里会是x(k+1)x(k+1)x(k+1),也就是下一状态,其实都是一样的
- 戴帽子的其他变量都是模型预测值
- eobs{e}_{obs}eobs:预测的误差,我们希望它越小越好。
从下图可以看出,通过调节A−KCA-KCA−KC我们可以让我的估计误差以指数性质逼近实际值
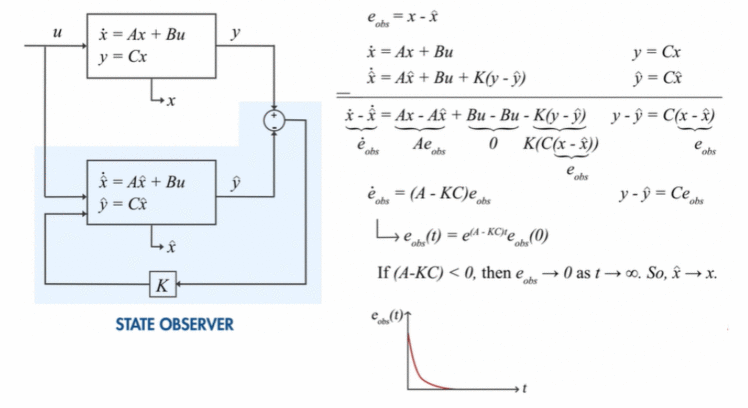
没有KKK其实也可以,但是有了KKK可以更方便调节,也更快

Kalman Filters
自动驾驶的例子也是相似的,只不过多了两个噪声wkw_kwk、vkv_kvk,他们满足正态分布。从概率分布来看,通过将预测值x^k\hat{x}_kx^k和观察值yky_kyk的概率分布相乘,我们可以得到一个更可靠的预测值x^k\hat{x}_kx^k
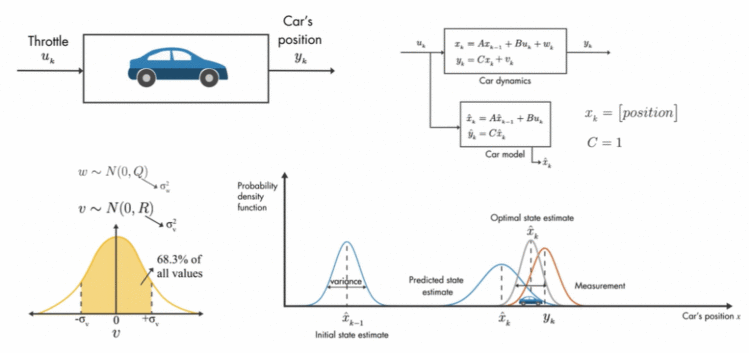
从State observer到Kalman filter,Kalman filter其实就是一种State observer。
- x^k−\hat{x}^-_kx^k−:模型预测值的预测值
- x^k\hat{x}_kx^k:同时考虑测量值和模型预测值的预测值
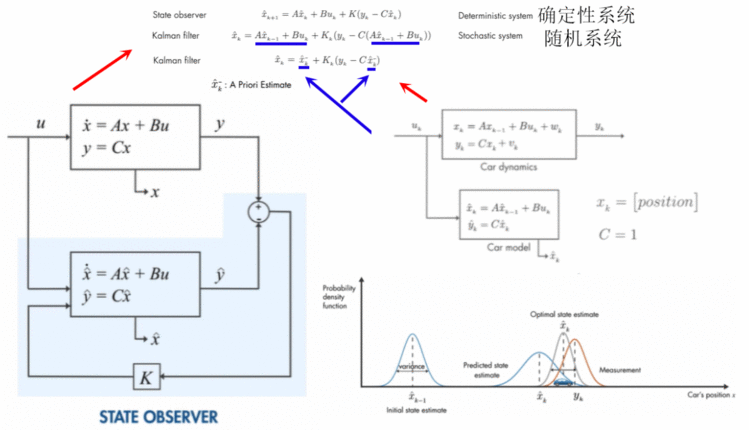

Kalman filter是处理一种动态的过程,也就是不断有新的观测值和测量值,要不断地更新预测值,不断地靠近真实值,如何更新呢 - Pk{P}_kPk:模型预测值x^k\hat{x}_kx^k的variance(变动)
- QQQ、RRR:白噪声的方差,也是一种变动
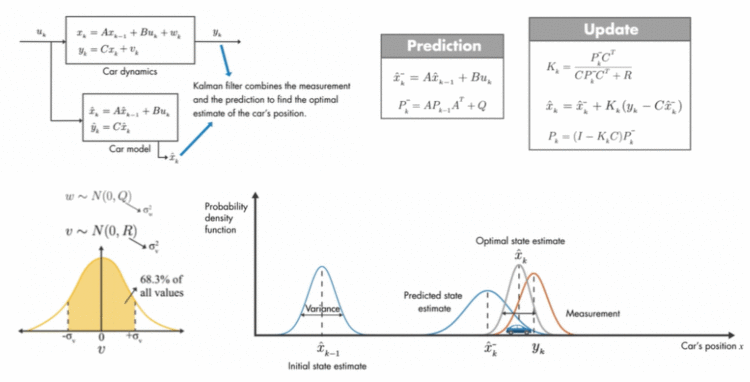
更新过程: - 知道了AAA、BBB、QQQ、u1{u}_1u1、P0{P}_0P0(初始值)、x^0−\hat{x}^-_0x^0−(初始值),可以得到x^1−\hat{x}^-_1x^1−、P1−{P}^-_1P1−
- 知道了CCC、RRR、计算得到的P1−{P}^-_1P1−,算出K1{K}_1K1、P1{P}_1P1,根据你的测量值y1{y}_1y1,计算同时考虑了模型前预测值、测量的后预测值
- 周而复始
视频介绍了两种极端情况便于理解。
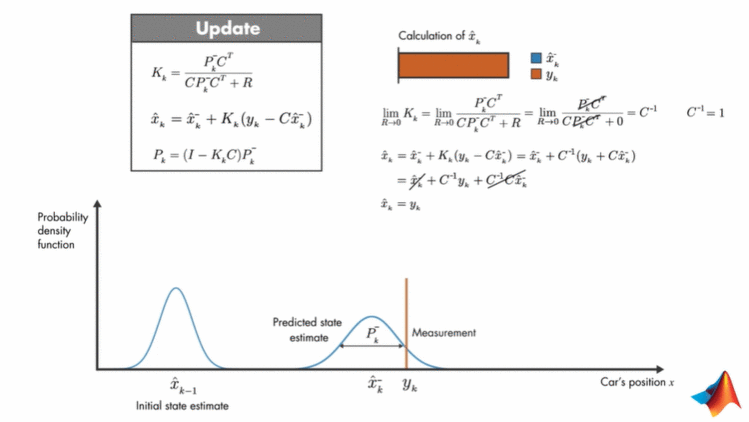
RRR=0,这说明测量时,内部温度到外部温度的转移模型非常好,基本没有噪声,那测量值的可信度就非常高
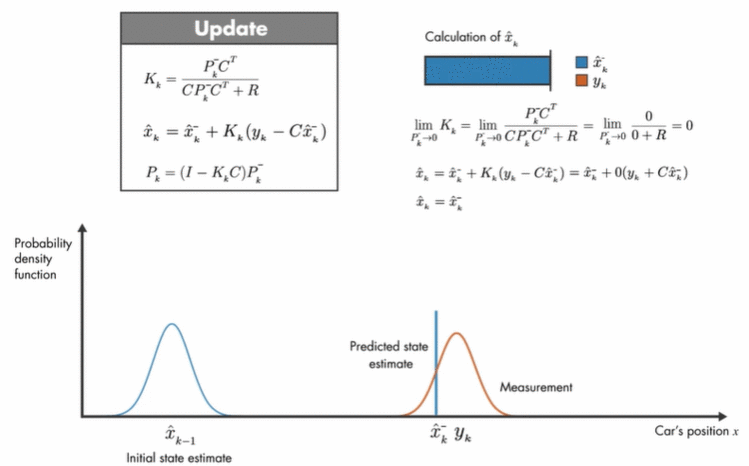
Pk−{P}^-_kPk−=0,这说明数学模型很好,预测出来的变化很小,预测的可信度很高
这些公式怎么推导的?数学不好,请自行搜索
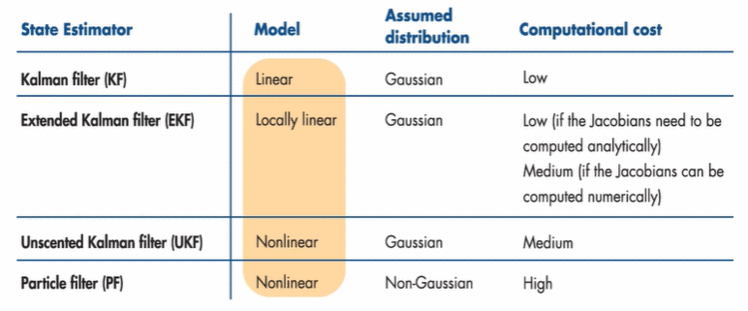
EKF、UKF、PF
KF是针对线性系统的,对于非线性系统,又出现了一些扩展