[COCI20112012#4]OGRADA题解

看到有大小关系限制，考虑拓扑排序，并在拓扑的同时从大到小进行填数。

问题转换为，对于拓扑队列中的所有元素（即 \(B'\) 的位置），应该把最大的数填在哪个位置上。

然后快快乐乐分类讨论就行了。

约定： 蓝色块为已填，灰色块为可填（在拓扑队列中），白色块为不能填（不在拓扑队列中），优先级越小越先填。

• \(A_{i-1}>A_i

  

  此时 \(B'_i\) 的值越小越好，并且 \(B'_i\) 的值每减小 \(1\)，答案增加 \(2\)，优先级为 \(4\)。

  
  



• \(A_{i-1}>A_i>A_{i+1}:\)

  

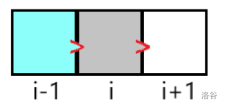
  此时从 \(B'_{i-1}\) 到 \(B'_{i+1}\) 对答案的贡献为 \(B'_{i-1}-B'_{i+1}\)，与 \(B'_{i}\) 无关，优先级为 \(2\)。

  
  



• \(A_{i-1} 与 \(A_{i-1}>A_i>A_{i+1}\) 同理。

  
  



• \(A_{i-1}A_{i+1}:\)

  

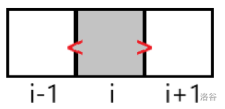
  此时 \(B'_i\) 的值越大越好，并且 \(B'_i\) 的值每增加 \(1\)，答案增加 \(2\)，优先级为 \(0\)。

  
  



• \(i=1,A_i>A_{i+1}:\)

  

  此时 \(B'_i\) 的值越大越好，并且 \(B'_i\) 的值每增加 \(1\)，答案增加 \(1\)，优先级为 \(1\)。

  
  



• \(i=1,A_i

  

  此时 \(B'_i\) 的值越小越好，并且 \(B'_i\) 的值每减小 \(1\)，答案增加 \(1\)，优先级为 \(3\)。

  
  



• \(i=n\) 与 \(i=1\) 同理。

  
  

拓扑的时候用优先队列，按照优先级排序即可。

（其实这玩意儿写出来更像 \(\text{Dijstra}\) /qd）

代码

分类讨论很麻烦，但代码不复杂。

#include
#define ll long long
using namespace std;
const int maxn=300010;
inline int read(){
int x=0;
char c=getchar();
for(;!(c>='0'&&c<='9');c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+c-'0';
return x;
}
struct edge{
int v,to;
}e[maxn<<1];
int head[maxn],ecnt;
void addedge(int u,int v){
e[++ecnt].v=v,e[ecnt].to=head[u],head[u]=ecnt;
}
priority_queue

,vector

>,greater

> >q;
bitsetvis;
int ru[maxn],n;
int a[maxn],b[maxn];
int Ans[maxn];
int Num(int i){
//返回对应位置优先级
if(i-1&&i if(!Ans[i-1]&&!Ans[i+1]) return 0;
if(Ans[i-1]&&Ans[i+1]) return 4;
return 2;
}
if(i-1){
if(Ans[i-1]) return 3;
return 1;
}
if(Ans[i+1]) return 3;
return 1;
}
void Solve(){
for(int i=1;i<=n;i++)
if(!ru[i]) q.push(make_pair(Num(i),i));
pairt;
int cnt=0;
//拓扑排序写法参考Dijstra堆优化版本
while(!q.empty()){
t=q.top(),q.pop();
if(vis[t.second]) continue;
//填过,continue
if(Num(t.second)^t.first) continue;
//不是当前状态(不是最新版本),continue
Ans[t.second]=b[++cnt],vis[t.second]=1;
if(t.second-1&&!ru[t.second-1])
q.push(make_pair(Num(t.second-1),t.second-1));
if(t.second q.push(make_pair(Num(t.second+1),t.second+1));
for(int i=head[t.second];i;i=e[i].to){
ru[e[i].v]--;
if(!ru[e[i].v])
q.push(make_pair(Num(e[i].v),e[i].v));
}
}

}
int main(){
n=read();
for(int i=1;i<=n;i++)
a[i]=read();
for(int i=1;i<=n;i++)
b[i]=read();
sort(b+1,b+1+n,greater());
for(int i=1;i if(a[i]>a[i+1])
addedge(i,i+1),ru[i+1]++;
else addedge(i+1,i),ru[i]++;
Solve();
ll ans=0;
for(int i=1;i ans+=abs(Ans[i]-Ans[i+1]);
printf("%lld\n",ans);
for(int i=1;i<=n;i++)
printf("%d ",Ans[i]);
return 0;
}