snake模型

转自：https://blog.csdn.net/caoniyadeniniang/article/details/77803002

一、曲线演化理论

   假设C=C(p)是一条光滑封闭的曲线，P是任意的参数化变量，设K表示曲 率，T表示切线，N表示法线，则有如下关系存在：

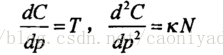
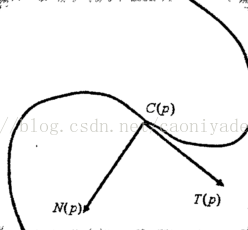
因为T和N是互相垂直的(如图所示)，所以平面上任何曲线都可以用曲 线上任何一点的T和N的线性组合来表示。在这里引入时间变量t，则曲线随时 间t的演化方程可用如下偏微分方程来表达：

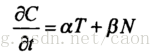
其中，切线方向的速度仅改变曲线的参数化，只有法向 的速度才改变的曲线地 形状（这句话百思不得琪姐，你们自己悟去吧）。仅考虑曲线地形状改变的话，上述方程可以改写为

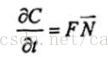
其中F是曲线地速度函数，N是法向量方向，如下图箭头所示，方程的意义即为曲线上个点沿着箭头方向以速度F运动。从而导致曲线形状发生变化。

二、snake 模型
   snake模型是基于参数的模型，轮廓的模型为C（s）,s为参数。snake模型与水平集模型都是基于能量的方法，其思想是以轮廓为参数构造能量，使轮廓在与目标重合的时候能量最小，不重合的时候始终大于零。通过最小化能量方程，即可求出目标的轮廓.
以下图为例,红色线是初始轮廓，绿色线为轮廓的法向量N，带分割的区域为黑色三角形。

则我们对每个点构造能量如下所示，其中第一项为轮廓点的斜率的平方，第二项为轮廓点二阶导数的平方，第三项为轮廓点处的的图像梯度。两个参数均大于0

这样，当轮廓处于无论处于目标的内部还是外部，其能量总是大于0，只有当两者重合时，能量才会最小。我们可以通过最小化包含曲线方程C的方程，求得能量最小化时曲线C的方程，即为待求目标的轮廓。
snake模型的能量分为内部能量与外部能量，内部能量即为曲线的一阶导数与二阶导数的平方项，用于控制轮廓的平滑度（曲线不平滑会使倒数项增大，造成内部能量增大。最小化能量则要求曲线尽量平滑，内部能量尽可能小）。外部能量通常为轮廓处的图像梯度，用于将轮廓向目标出牵引。如上图所示，当轮廓完全位于目标的外部或内不是，轮廓处的图像梯度均为0，只有在目标的轮廓出会发生梯度的突变。最小化能量要求轮廓尽可能与目标的轮廓重合，此时外部能量想最小。下面对snake模型进行推导
其中 曲线表示为V（s）,s为参数 vs, vss 分别为轮廓的一阶导数与二级倒数。
轮廓的总能量为关于v,vs，vss的泛函。

带人得：

--------------------- 
作者：林中漫 
来源：CSDN 
原文：https://blog.csdn.net/caoniyadeniniang/article/details/77803002 
版权声明：本文为博主原创文章，转载请附上博文链接！