今天,给大家介绍一个“模型”,帮助大家进一步的理解有理数的加、减法法则.
一、模型:用○表示﹢1,则○○表示﹢2,○○○表示﹢3,…;
用●表示﹣1,则●●表示﹣2,●●●表示﹣3….
规定:●+○=○+● =0,●●+○○=○○+●●=0….
二、用模型解释有理数的加法
1.先来看同号两数相加的情况
(1)○○+○○○=○○○○○ 写成算式为:2+3=5;
(2)●●+●●●=●●●●● 写成算式为:(﹣2)+(﹣3)=﹣5.
显然,正数加正数,结果为正数,负数加负数,结果为负数,即同号两数相加,取相同符号,并把绝对值相加.
2.再来看异号两数相加的情况
(3)○○+●●●=○○+●●●=● 写成算式为:2+(-3)=-1;
●●●+○○=●●●+○○=● 写成算式为:(-3)+2=-1.
(4)●●+○○○=●●+○○○=○ 写成算式为:(﹣2)+3=1;
○○○+●●=○○○+●●=○ 写成算式为:3+(﹣2)=1.
显然,异号两数相加的实质就是比多少,若正数个数多,则结果为正数;若负数个数多,则结果为负数;若个数一样多,则由规定可知,结果为零.即绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,互为相反数的两个数相加得零.
3.最后看一个数与零相加的情况
易知,0+○=○+0=○ 写成算式为:0+1=1+0=1,
0+●=●+0=● 写成算式为:0+(-1)=(-1)+0=(-1).
显然,一个数与零相加仍得这个数.
三、用模型解释有理数的减法
1.先来看同号两数相减的情况
(1)○○-○=○ 写成算式为:2-1=1;
○○-○○=0 写成算式为:2-2=0;
○-○○=0-○=(●+○)-○=● 写成算式为:1-2=﹣1.
显然,正数减正数,若被减数的个数比减数的个数多,结果为正数;若被减数的个数与减数的个数一样多,结果为零;若被减数的个数比减数的个数少,结果为负数;而差的绝对值就是被减数比减数多或少的个数.
(2)●●-● =● 写成算式为:(﹣2)+(﹣1)=﹣1.
●●-●●=0 写成算式为:(﹣2)-(﹣2)=0.
●-●●=0-●=(●+○)-●=○ 写成算式为:(﹣1)-(﹣2)=1.
显然,负数减负数,若被减数的个数比减数的个数多,结果为负数;若被减数的个数与减数的个数一样多,结果为零;若被减数的个数比减数的个数少,结果为正数,而差的绝对值就是被减数比减数多或少的个数.
综上,我们可以归纳为:同号两数相减,把绝对值相减,若不够减,则转化为零减去一个数,且零减去正数得(与它相反的数)负数,零减去负数得(与它相反的数)正数.
2.再来看异号两数相减的情况
(3)○-●● =○+0-●●=○+(○○+●●)-●●
=○+○○=○○○
即1 -(-2)=1+2=3;
(4)●●-○=●●+0-○=●●+(○+●)-○
=●●+●=●●●
即(-2)- 1=(-2)+(-1)=(-3).
显然,正数减负数差为正,负数减正数差为负,且绝对值相加.即异号两数相减的实质就被减数加上减数的相反数.
事实上,《九章算术》的方程一章中,就提出了如下的“正负数”:
同名相除,异名相益,正无入负之,负无人正之.不难看出,这与我们上面所说的有理数的减法法则是完全一致的.即
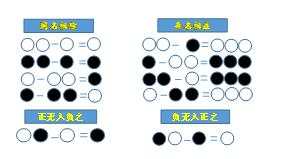
实际上,《九章算术》中,还提出了关于正负数和零的加法运算法则:其异名相除,同名相益,正无入正之,负无入负之.你能把它翻译成现在的语言吗?
3.从异号两数相减中,我们发现,减法可以转化为加法,那么任意两数相减是否也能转换成加法呢?
我们来看一般情形:
a-1可以用模型表示为a-○=a+0-○=a+(●+○)-○
=a+●
即a-1=a+(-1)
a-2可以用模型表示为a-○○=a+0-○○=a+(●●+○○)-○○
=a+●●
即a-2=a+(-2)
……
a-(-1)可以用模型表示为a-●=a+0-●=a+(●+○)-●
=a+○
即a-(-1)=a+1
a-(-2)可以用模型表示为a-●●=a+0-●●=a+(●●+○○)-●●
=a+○○
即a-(-2)=a+2
……
进而,我们得到a-b=a+(-b).
这样,有理数的减法,就转化为有理数的加法,于是有理数的减法则就可以概括为:减去一个数等于加上这个数的相反数.这样,有理数的加、减法就统一成了加法.

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有