matlab皮尔逊和斯皮尔曼,利用matlab计算Pearson和Spearman相关系数

Pearson相关系数

考察两个事物(在数据里我们称之为变量)之间的相关程度&＃xff0c;简单来说就是衡量两个数据集合是否在一条线上面。其计算公式为&＃xff1a;

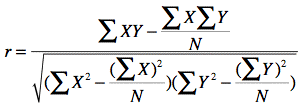或或

N表示变量取值的个数。

相关系数r的值介于–1与&＃43;1之间&＃xff0c;即–1≤r≤&＃43;1。其性质如下&＃xff1a;

当r>0时&＃xff0c;表示两变量(当X的值增大(减小)&＃xff0c;Y值增大(减小))正相关&＃xff0c;r<0时&＃xff0c;两变量为负相关(当X的值增大(减小)&＃xff0c;Y值减小(增大))。

当|r|&＃61;1时&＃xff0c;表示两变量为完全线性相关&＃xff0c;即为函数关系。

当r&＃61;0时&＃xff0c;表示两变量间无线性相关关系。

当0

当两个变量的标准差都不为零时&＃xff0c;相关系数才有定义&＃xff0c;皮尔逊相关系数适用于&＃xff1a;

两个变量之间是线性关系&＃xff0c;都是连续数据。

两个变量的总体是正态分布&＃xff0c;或接近正态的单峰分布。

两个变量的观测值是成对的&＃xff0c;每对观测值之间相互独立。

一个具体的计算例子&＃xff1a;

X Y

1 2

2 5

3 6

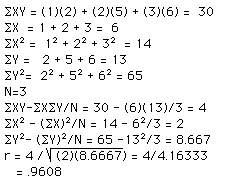
而利用matlab计算的话则可以使用函数 corrcoef或corr

先看一下help corrcoef的内容&＃xff1a;

再看一下help corr的内容

对于前面提到的具体的计算例子&＃xff0c;可以在matlab中实现如下&＃xff1a;

x&＃61;[1;2;3];

y&＃61;[2;5;6];

r1&＃61;corr(x,y,&＃39;type&＃39;,&＃39;pearson&＃39;);

r2&＃61;corrcoef(x,y);最后可以看到

r1&＃61;0.9608

r2&＃61;

1.0000 0.9608

0.9608 1.0000

均与前面的计算结果相符。需要注意的是&＃xff0c;使用corr函数时默认计算皮尔逊相关系数

Spearman相关系数

斯皮尔曼相关系数用来估计两个变量X、Y之间的相关性&＃xff0c;其中变量间的相关性可以使用单调函数来描述。如果两个变量取值的两个集合中均不存在相同的两个元素&＃xff0c;那么&＃xff0c;当其中一个变量可以表示为另一个变量的很好的单调函数时(即两个变量的变化趋势相同)&＃xff0c;两个变量之间的相关系数可以达到&＃43;1或-1。

假设两个随机变量分别为X、Y(也可以看做两个集合)&＃xff0c;它们的元素个数均为N&＃xff0c;两个随机变量取的第i(1<&＃61;i<&＃61;N)个值分别用Xi、Yi表示。对X、Y进行排序(同时为升序或降序)&＃xff0c;得到两个元素排行集合x、y&＃xff0c;其中元素xi、yi分别为Xi在X中的排行以及Yi在Y中的排行。将集合x、y中的元素对应相减得到一个排行差分集合d&＃xff0c;其中di&＃61;xi-yi&＃xff0c;1<&＃61;i<&＃61;N。随机变量X、Y之间的斯皮尔曼相关系数可以由x、y或者d计算得到&＃xff0c;其计算方式如下所示&＃xff1a;

由排行差分集合d计算而得(公式一)&＃xff1a;

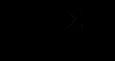
由排行集合x、y计算而得(斯皮尔曼相关系数同时也被认为是经过排行的两个随机变量的皮尔逊相关系数&＃xff0c;以下实际是计算x、y的皮尔逊相关系数)(公式二)&＃xff1a;

以下是一个计算集合中元素排行的例子(仅适用于斯皮尔曼相关系数的计算)

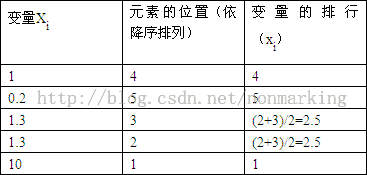
这里需要注意&＃xff1a;当变量的两个值相同时&＃xff0c;它们的排行是通过对它们位置进行平均而得到的。

斯皮尔曼相关系数对数据条件的要求没有皮尔逊相关系数严格&＃xff0c;只要两个变量的观测值是成对的&＃xff0c;或者是由连续变量观测资料转化得到的&＃xff0c;不论两个变量的总体分布形态、样本容量的大小如何&＃xff0c;都可以用斯皮尔曼相关系数来进行研究。

使用matlab计算spearman相关系数则比较简单&＃xff0c;也是使用corr函数&＃xff0c;如下&＃xff1a;

r&＃61; corr(x, y, &＃39;type&＃39; , &＃39;Spearman&＃39;);

对于上面的例子&＃xff0c;则可以计算出r&＃61;1。

注意&＃xff1a;使用Matlab自带函数计算斯皮尔曼相关系数时&＃xff0c;需要保证X、Y均为列向量&＃xff1b;Matlab自带的函数是通过公式二计算序列的斯皮尔曼相关系数的。