matlab计算机械臂素的,机械臂动力学——动力学建模

一、动力学基础概念

基本动力学模型

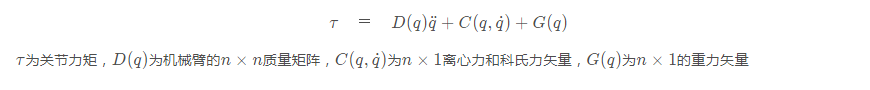
建模方法

牛顿-欧拉法

拉格朗日法

连杆质量，连杆质心位置矢量，连杆质心惯性矩阵(通过动力学参数识别获得)

二、牛顿-欧拉法

运动外推：向外迭代计算连杆的角速度、角加速度和线加速度

力外推：计算作用在连杆质心上的惯性力和力矩

力矩内推：向内迭代计算关节力矩

2.1 运动向外迭代

2.1.1 刚体线速度和角速度

线速度

坐标系{A}为固定，坐标系{B}固连在刚体上。

2.1.2 连杆速度

连杆i+1的速度为连杆i的速度加上附加到关节i+1上的速度分量。

注意：线速度相对于一点，角速度相对于一个物体，因此，"连杆的速度“指连杆坐标原点的线速度和连杆的角速度

角速度

连杆i+1的角速度等于连杆i的角速度加上一个由于关节i+1上的角速度引起的分量。

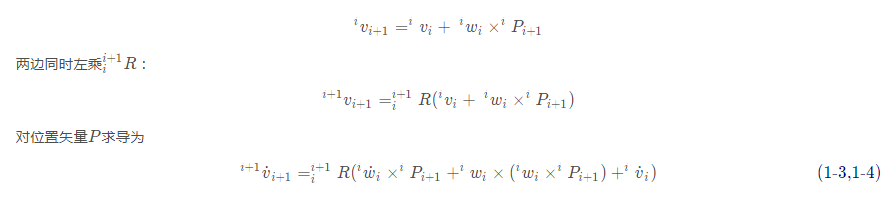
2.2 力向外迭代

2.2.1 牛顿方程(Newton)

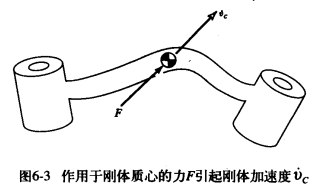
用于描述刚体的平动。

质点的牛顿方程

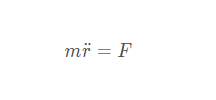
m为质点质量，r为矢径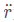，为加速度，F为质点的合力。

平动刚体的牛顿方程

刚体平动为刚体上每一点速度一致。

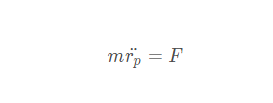
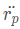为刚体上任一点加速度。

一般运动刚体的牛顿方程

刚体平动为刚体上各点速度不相同。

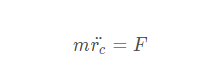
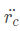为刚体质心的加速度。

2.2.2 欧拉方程(Euler方程)

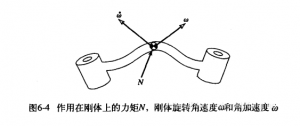
绕定点转动刚体的Euler方程

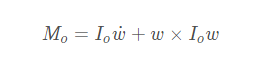
w为刚体固连坐标系的角速度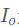，为常值矩阵，表示刚体在与刚体固连坐标系中对O点的惯性张量矩。

2.3 力和力矩向内迭代

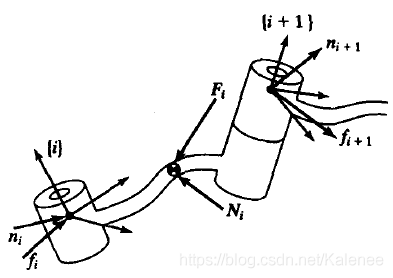
上图为典型连杆在无重力状态下受力图，根据该图建立力平衡方程和力矩平衡方程。

力平衡方程

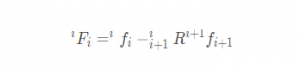
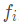为连杆i-1作用在连杆i上的力

力矩平衡方程

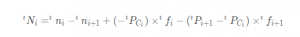
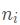为连杆i-1作用在连杆i上的力矩

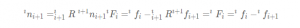
根据力平衡方程和附加旋转矩阵可化简该公式

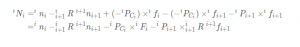
迭代方程

按照连杆序号高到低排序获得迭代关系为

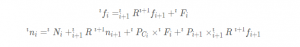
2.4 建立动力学方程

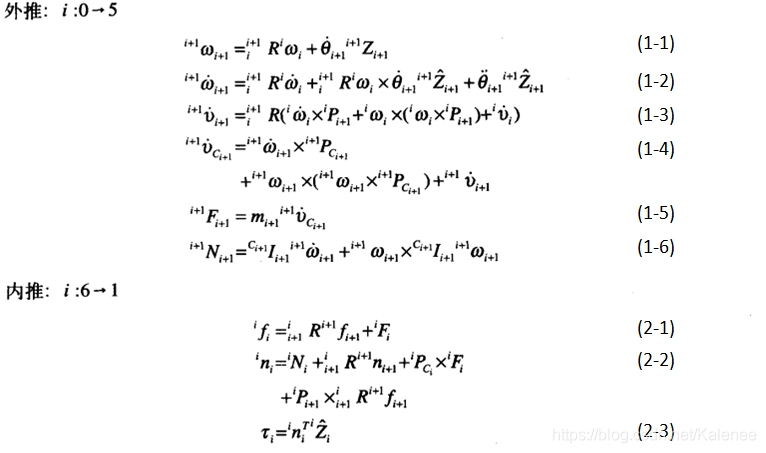
2.5 两连杆动力学方程

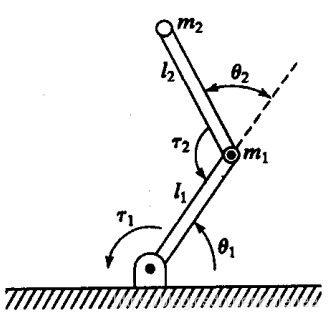
假设连杆质量集中在连杆末端，质量分别为m 1​和m2​。

连杆质心位置矢量

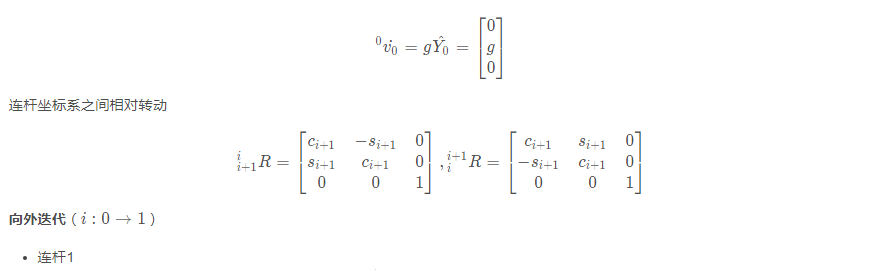
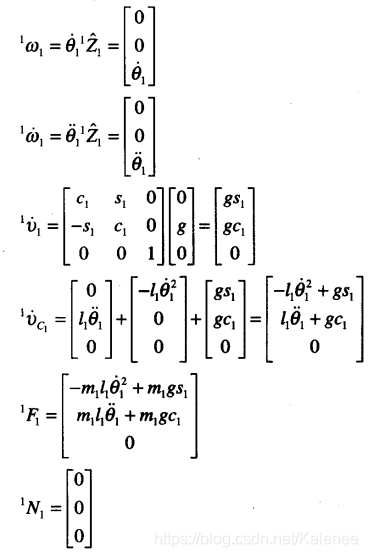
连杆2

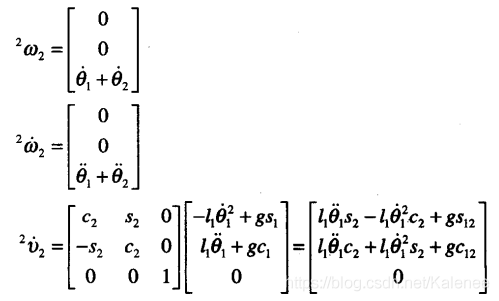
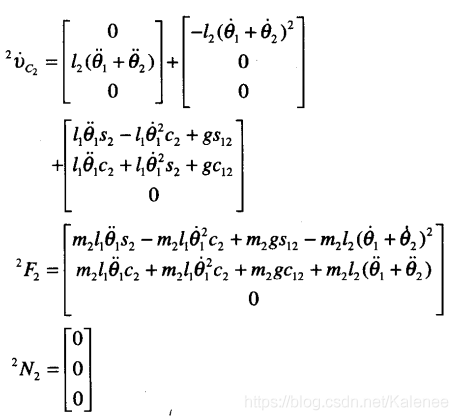
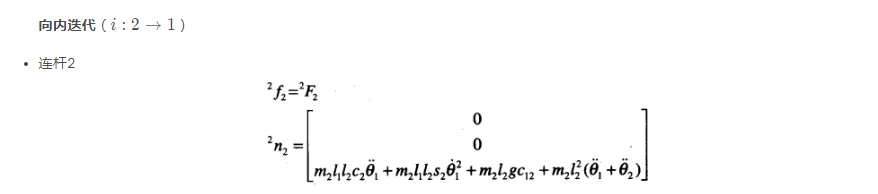
连杆1

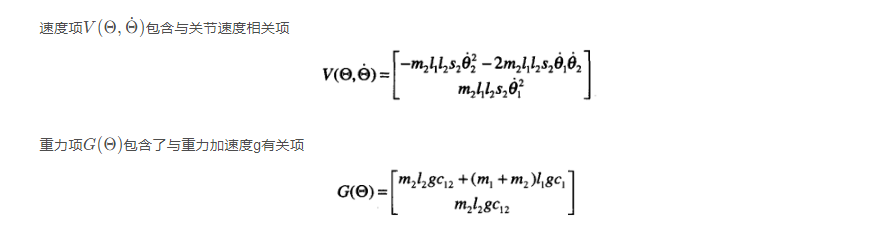
Matlab建模

% 动力学建模

syms l1 l2 m1 m2 g;

syms q1 q2 dq1 dq2 ddq1 ddq2;

%% 参数初始化

R{1}=[cos(q1) -sin(q1) 0;sin(q1) cos(q1) 0;0 0 1];

R{2}=[cos(q2) -sin(q2) 0;sin(q2) cos(q2) 0;0 0 1];

R{3}=[1 0 0;0 1 0;0 0 1];

% 坐标系原点位移，用P{1}表示坐标系1与坐标系0原点位置关系，用P{2}表示坐标系2与坐标系1原点位置关系。

P = cell(1,3);

P{1}=[0;0;0];P{2}=[l1;0;0];P{3}=[l2;0;0];

% 每个连杆质心的位置矢量

Pc = cell(1,3);

Pc{1}=[0;0;0];Pc{2}=[l1;0;0];Pc{3}=[l2;0;0];

% 连杆质量

m = cell(1,3);

m{2}=m1;

m{3}=m2;

% 惯性张量

I = cell(1,3);

I{2}=[0;0;0];

I{3}=[0;0;0];

% 连杆间角速度和角加速度

w = cell(1,3);dw = cell(1,3);

w{1}=[0;0;0];dw{1}=[0;0;0];% 机器人底座不旋转

% 连杆坐标原点和质心加速度

dv = cell(1,3);dvc = cell(1,3);

dv{1}=[0;g;0];% 重力因素

% 关节速度和加速度

dq = cell(1,3); ddq = cell(1,3);

dq{2}=[0;0;dq1];dq{3}=[0;0;dq2];

ddq{2}=[0;0;ddq1];ddq{3}=[0;0;ddq2];

% 末端执行器没有力

f = cell(1,4);n = cell(1,4);

f{4}=[0;0;0];

n{4}=[0;0;0];

%% 建立运动学方程

% 外推

for i=1:2 %matlab下标从1开始

w{i+1}=R{i}.&＃39;*w{i}+dq{i+1};

dw{i+1}=R{i}.&＃39;*dw{i}+cross(R{i}.&＃39;*w{i},dq{i+1})+ddq{i+1};

dv{i+1}=R{i}.&＃39;*(cross(dw{i},P{i})+cross(w{i},cross(w{i},P{i}))+dv{i});

dvc{i+1}=cross(dw{i+1},Pc{i+1})+cross(w{i+1},cross(w{i+1},Pc{i+1}))+dv{i+1};

F{i+1}=m{i+1}*dvc{i+1};

N{i+1}=[0;0;0];%假设质量集中，每个连杆惯性张量为0

end

% 内推

for i=3:-1:2

f{i}=R{i}*f{i+1}+F{i};

n{i}=N{i}+R{i}*n{i+1}+cross(Pc{i},F{i})+cross(P{i},R{i}*f{i+1});

end

% 力矩

tau = cell(1,2);

tau{1} = n{2}(3);

tau{2} = n{3}(3);

celldisp(tau)

三、拉格朗日法

拉格朗日法为基于能量的动力学方法。

3.1 动能

第i根连杆的动能k i k_iki​为连杆质心线速度产生动能和连杆角速度产生动能之和

3.3 构建动力学方程

拉格朗日函数定义为系统的动能减去势能

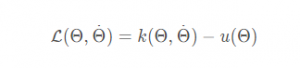
操作臂运动方程为

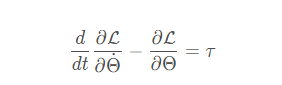
τ为n x 1力矩矢量，运动方程代入拉格朗日函数为

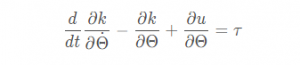
3.4 两连杆动力学方程

2R机械臂在处在xy平面内，重力沿-y方向。

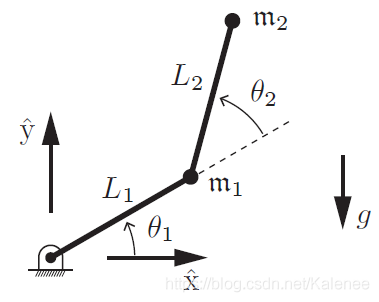
连杆质心线速度

连杆1

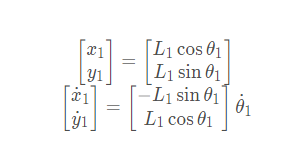
连杆2

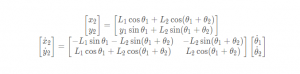
连杆角速度

因质量集中，连杆质心惯性张量为零矩阵

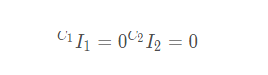
因此连杆角速度产生动能为0，即

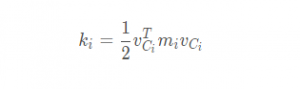
连杆动能

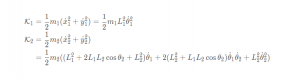
连杆势能

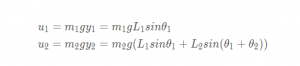
拉格朗日方程

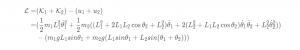
使用运动方程求力矩

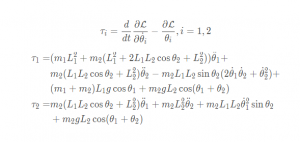
状态空间方程

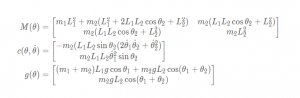
matlab建模

% 质量集中，无惯性矩阵，连杆长度与质心位置重合

syms m1 m2 l1 l2 g

syms q1 q2 q1d q2d q1dd q2dd

syms x1(t) x1d x1dd x2(t) x2d x2dd

x1d=diff(x1,t); x2d=diff(x2,t);

x1dd=diff(x1,t,t); x2dd=diff(x2,t,t);

%质量矩阵

M1=diag([m1,m1]);

M2=diag([m2,m2]);

% 速度

V1=[[l1*cos(x1(t)) 0];[l1*sin(x1(t)) 0]]*[x1d;x2d];

V2=[[-l1*sin(x1(t))-l2*sin(x1(t)+x2(t)) -l2*sin(x1(t)+x2(t))];

[l1*cos(x1(t))+l2*cos(x1(t)+x2(t)) l2*cos(x1(t)+x2(t))]]*[x1d;x2d];

% 动能

K1=simplify((1/2)*V1.&＃39;*M1*V1);

K2=simplify((1/2)*V2.&＃39;*M2*V2);

K =K1+K2;

% 势能

u1=m1*g*l1*sin(q1);

u2=m2*g*(l1*sin(q1)+l2*sin(q1+q2));

u =u1+u2;

% 拉格朗日方程

L=K-u;

L=subs(L,{x1,x2,x1d,x2d,x1dd,x2dd},{q1,q2,q1d,q2d,q1dd,q2dd});

% 利用运动方程计算力矩方程

dLdqd=[diff(L,q1d); diff(L,q2d)];

dLdqd =subs(dLdqd, {q1,q2,q1d,q2d,q1dd,q2dd}, {x1,x2,x1d,x2d,x1dd,x2dd});

ddLdqddt=diff(dLdqd,t);

ddLdqddt= subs(ddLdqddt,{x1,x2,x1d,x2d,x1dd,x2dd},{q1,q2,q1d,q2d,q1dd,q2dd});

dLdq=[diff(L,q1); diff(L,q2)];

% 输出结果

syms f

f=simplify(ddLdqddt-dLdq)

四、算法对比

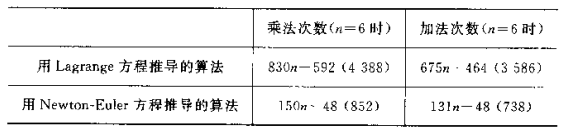
通过牛顿欧拉方程导出的逆动力算法较拉格朗日方程推导计算量要少，但实际上两者差异在于表示连杆角速度的方式不一致，牛顿欧拉方程采用三维矢量，拉格朗日方程采用3 × 3 3 \times 33×3旋转矩阵导数，因此多余因素造成计算量增大，若在计算动能时采用三维角速度矢量描述，则拉格朗日方程可推导处与牛顿欧拉方程相同的形式的逆动力方程。

在实际应用中，多轴机械臂连杆结合计算机建模更适合选用牛顿-欧拉法，手动推算下拉格朗日法更加简单直观，但推导多轴机械臂较为困难。

参考

MATLAB机器人运动学与动力学

MATLAB 中的机械臂算法——动力学

三关节机械臂动力学模型问题？

【机器人学】机器人开源项目KDL源码学习：(4)机械臂逆动力学的牛顿欧拉算法

matlab递推牛顿-欧拉法解机械臂动力学方程

《机器人动力学与控制》第九章——动力学 9.1初探欧拉拉格朗日方程法

机器人动力学–拉格朗日公式

《机器人动力学与控制》

《机器人技术基础》

《机器人学导论》

Kenvin M. Lynch , Frank C. Park, Modern Robotics Mechanics,Planning , and Control. May 3, 2017