论文地址&＃xff1a;Learning Identity Mappings with Residual Gates
本文地址&＃xff1a;http://blog.csdn.net/wspba/article/details/72789964

前言

自从2015年ResNet在ImageNet比赛上火了之后&＃xff0c;现在简直就是大红大紫啊&＃xff0c;这两年关于ResNet的研究、基于ResNet网络的延伸、改进也越来越多&＃xff0c;包括FractalNet、WideResNet、DenseNet等等&＃xff0c;这几篇文章都会一一为大家介绍&＃xff0c;今天要介绍的叫做Gated ResNet&＃xff0c;它来自一篇发表在今年ICLR上的论文&＃xff0c;它没有之前提到的几个网络复杂&＃xff0c;它对ResNet所提出的Identity Mapping进行了更加细致的思靠&＃xff0c;它认为Identity Mapping才是ResNet包括Highway Network的精髓&＃xff0c;并提出了对于一个深层网络&＃xff0c;如果它具有退化成Identity Mapping的能力&＃xff0c;那么它一定是容易优化、并且具有很好性能的。

精髓&＃xff1a;Identity Mapping

ResNet中所提出的Residual block之所以成功&＃xff0c;原因有两点&＃xff0c;第一&＃xff0c;是它的shortcut connection增加了它的信息流动&＃xff0c;第二&＃xff0c;就是它认为对于一个堆叠的非线性层&＃xff0c;那么它最优的情况就是让它成为一个恒等映射&＃xff0c;但是shortcut connection的存在恰好使得它能够更加容易的变成一个Identity Mapping。对于第二点&＃xff0c;其实刚开始看ResNet原文时&＃xff0c;并没有完全理解&＃xff0c;直到看到今天所讲的这篇论文时才正真理解到它的含义。

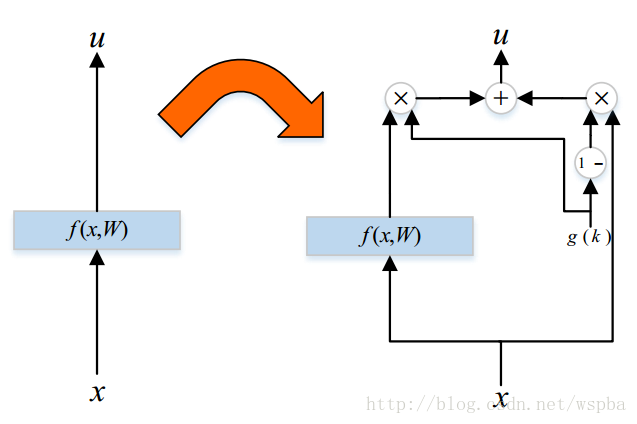
看下图&＃xff1a;

下面那行的网络其实就是在上面那行网络的基础上新叠加了一层&＃xff0c;而新叠加上那层的权重weight&＃xff0c;如果能够学习成为一个恒等的矩阵I&＃xff0c;那么其实上下两个网络是等价的&＃xff0c;那么也就是说如果继续堆叠的层如果能够学到一个恒等矩阵&＃xff0c;那么经过堆叠的网络是不会比原始网络的性能差的&＃xff0c;也就是说&＃xff0c;如果能够很容易的学到一个恒等映射&＃xff0c;那么更深层的网络也就更容易产生更好的性能。这是ResNet所提出的根源&＃xff0c;也是本文所强调的重点。

对于一个网络中的一个卷积层f(x,W)&＃xff0c;W是卷积层的权重&＃xff0c;如果要使得这个卷积层是一个恒等映射&＃xff0c;即f(x,W)&＃61;x&＃xff0c;那么W就应该是一个恒等映射I,但是当模型的网络变深时&＃xff0c;要使得W&＃61;I 就不那么容易。对于ResNet的每一个Residual Block&＃xff0c;要使得它为一个恒等映射&＃xff0c;即f(x,W)&＃43;x&＃61;x&＃xff0c;就只要使得W&＃61;0即可&＃xff0c;而学习一个全0的矩阵比学习一个恒等矩阵要容易的多&＃xff0c;这就是ResNet在层数达到几百上千层时&＃xff0c;依然不存在优化难题的原因。

改进&＃xff1a;Residual Gates

学习一个全0矩阵&＃xff0c;是要使得一个矩阵中所有的值都为0&＃xff0c;那么还有没有更简单的方法呢&＃xff1f;比如说&＃xff0c;只要一个值为0就够了&＃xff1f;这恰恰就是本文的亮点&＃xff1a;Residual Gates。

下图是基于plain network的一个改进&＃xff1a;

这样f(x,W)就变成了g(k)f(x,W)&＃43;(1-g(k))x&＃xff0c;很熟悉有没有&＃xff0c;是不是很像Highway Network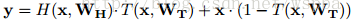&＃xff1a; &＃xff0c;但是Highway Network仍然需要学习一个以x为输入的函数T(x,Wt)&＃xff0c;使Wt为全0矩阵时&＃xff0c;整个网络才相当于恒等映射。而在这里&＃xff0c;只需要g(k)等于0表示为恒等映射&＃xff0c;注意到这里k也是模型的一个参数&＃xff0c;也是通过模型的前向和反向训练得出&＃xff0c;g为激活函数&＃xff08;ReLU&＃xff09;&＃xff0c;即只要k学习到一个接近于0或者小于0&＃xff08;由于ReLU的存在&＃xff09;的值&＃xff0c;或者k&＃61;1&＃xff0c;W&＃61;I即可&＃xff0c;比单纯指望W学习到I要简单得多。按照作者的意思&＃xff0c;这个模型就具有了退化成恒等映射的能力&＃xff0c;因此当层数加深时&＃xff0c;是能够提升模型的性能的。

而对于ResNet&＃xff0c;也可以使用同样的Gates&＃xff1a;

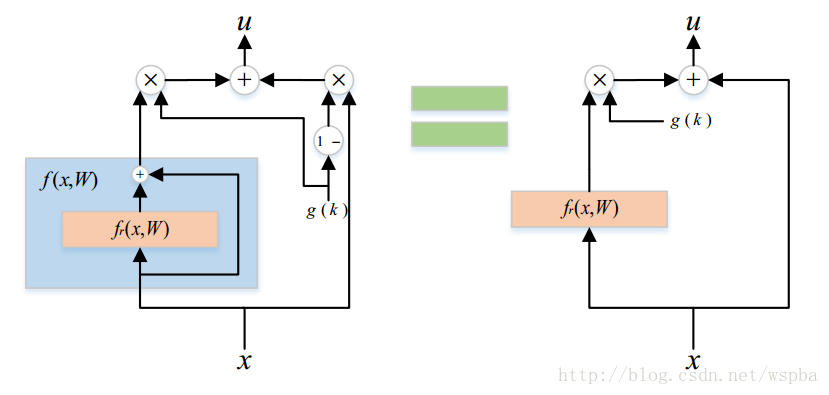
即&＃xff1a;g(k)(f(x,W)&＃43;x)&＃43;(1-g(k))x&＃61;g(k)f(x,W)&＃43;x ,这样看来g(k)甚至都不需要作为门控的功能&＃xff0c;只要相当于一个缩放的作用&＃xff0c;相比于原始ResNet需要W学成全0矩阵而言&＃xff0c;使得g(k)等于0更加简单&＃xff0c;因此作者推断&＃xff0c;门控版的Gates ResNet要强于原始的ResNet。

实验

模型在MINIST和CIFAR-10数据集上的结果在这里就不多进行展示和解释。但是有几点我也是比较感兴趣的。
首先&＃xff1a;

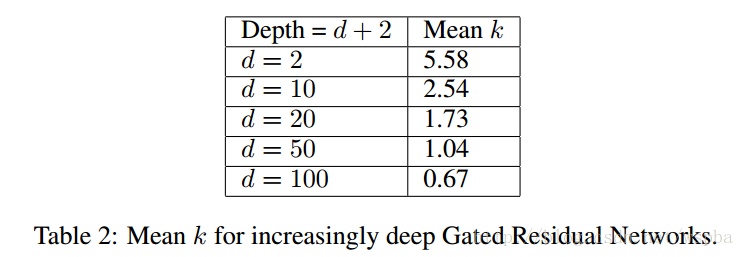
当模型较浅时&＃xff0c;参数优化简单&＃xff0c;因此k的作用体现不出来&＃xff0c;而且k值很大&＃xff0c;可能起到的是一个信号的放大或者增强的作用&＃xff1b;但是当层数逐渐增加时&＃xff0c;k值慢慢减小&＃xff0c;比如上图&＃xff0c;d&＃61;100时&＃xff0c;k的均值只有0.67&＃xff0c;那么在很多层中&＃xff0c;k的值应该是很接近与0的&＃xff0c;这些层起到的就是恒等映射的作用&＃xff0c;这也就验证了作者的观点。

其次&＃xff0c;另外一个图&＃xff0c;这是一个100层的深层模型&＃xff1a;

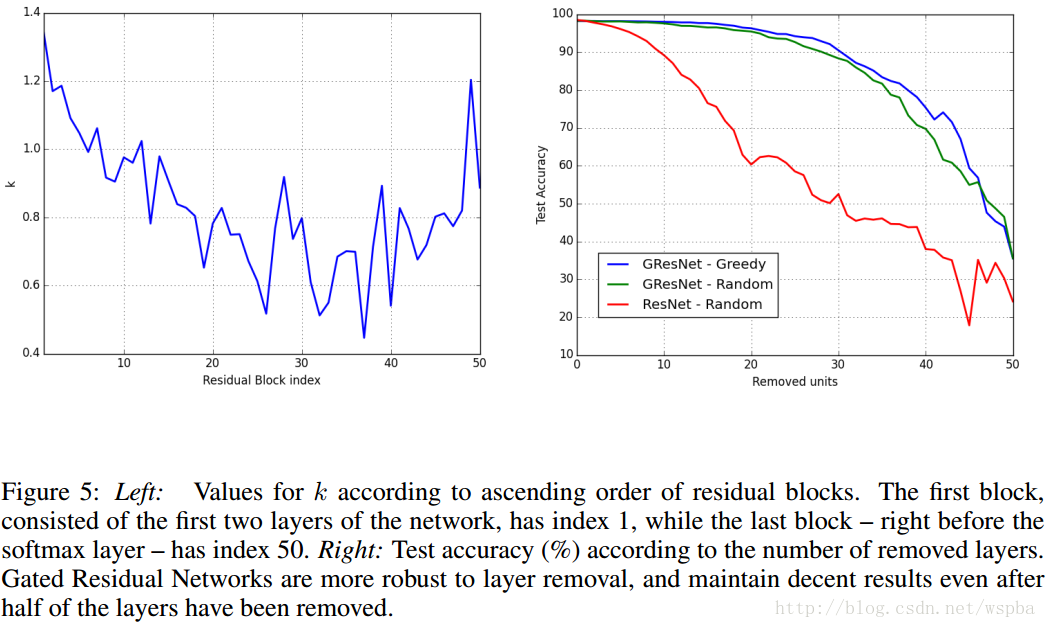
作者发现在ResNet中&＃xff0c;k值可能在中间的某些曾具有更低的值&＃xff0c;而作者认为&＃xff0c;当k接近于0时&＃xff0c;该层接近于恒等映射&＃xff0c;那么该层可能起到更多的就是信息传递&＃xff0c;而不是信息提取的作用&＃xff0c;因此&＃xff0c;对于整个模型的影响并不大&＃xff0c;那么将这些层剔除&＃xff0c;模型的性能应该也不会有太大的影响。右图的曲线也证明了这点&＃xff0c;作者的这个发现&＃xff0c;为模型的压缩也提供的新的思路。

基于第二个发现&＃xff0c;在只有24层的浅层模型中&＃xff1a;

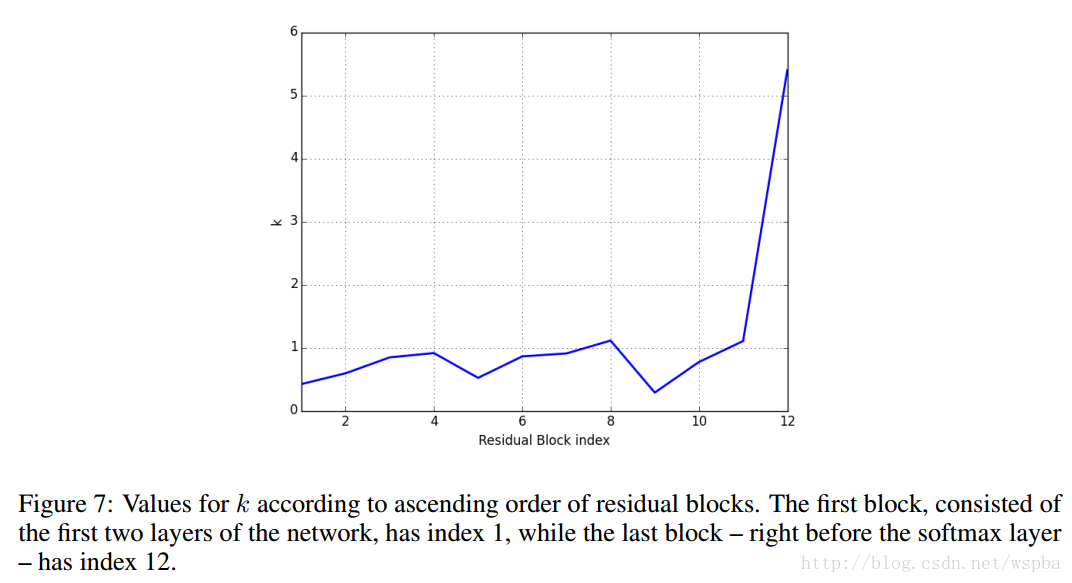
我们发现&＃xff0c;在第1、5、9个residual block中&＃xff0c;k值很低&＃xff0c;而第1、5、9个residual block正好对应了维度上升的层&＃xff08;不明白的可以回去看Wide ResNet或者ResNet的模型结构&＃xff09;&＃xff0c;这说明了在升维的residual block中&＃xff0c;shortcut connection中用来增加维度卷积层起到了更加重要的作用&＃xff0c;而在最后一个block中&＃xff0c;k值非常高&＃xff0c;也就是说明在这里&＃xff0c;shortcut connection几乎不起到作用&＃xff0c;因此将shortcut connection去除也几乎没有影响。

总结

这篇论文给模型的设计和优化提供了很好的思路&＃xff0c;它提出了一个叫做模型退化成恒等映射的能力&＃xff0c;即&＃xff0c;如果模型具有退化成恒等映射的能力&＃xff0c;那么堆叠很多这样的层&＃xff0c;将不会比更浅的层效果要差。提出了一个只有单一参数的门控机制&＃xff0c;它是的普通的平原网络&＃xff0c;甚至是本来就性能很好的ResNet&＃xff0c;变得更好&＃xff0c;原因是一个参数的学习总会比多维权重的学习更加简单。最后&＃xff0c;作者还给出了一个对模型理解以及优化的思路&＃xff0c;对于一个含有门控机制的训练好的模型&＃xff0c;我们可以通过观察k的值&＃xff0c;来判断各个层的作用&＃xff0c;并且根据作用的重要性&＃xff0c;可以对不重要的层进行剔除而不影响到模型的效果&＃xff0c;起到了一个模型压缩的作用。

总的来说&＃xff0c;这篇论文真的是非常棒的文章&＃xff0c;值得大家细细品读&＃xff0c;当然论文中还有很多理解不到位的地方&＃xff0c;也希望大家能够提出来&＃xff0c;一起交流一起学习&＃xff01;