假定用户使用某种产品符合以下的马尔可夫过程:改过程的状态为0和1,其中$s=0$表示用户不再使用该产品,$s=1$表示用户使用该产品。那么该马尔可夫过程的转移矩阵是$M=\begin{bmatrix}1 & 0 \\1-p & p \\\end{bmatrix}$。
假定初始状态是$s_1=1$,并且假定用户的使用次数(随机变量)为$X$,那么$Pr(X \ge k)=p^{k-1}$。
定义已经使用$k \ge 1$次该产品的用户的忠诚度为$S(k)=\frac{Pr(X \ge k+1)}{Pr(X \ge k)}$,表示已经使用了$k$次该产品的用户,会继续使用该产品的可能性。如果完全符合假设,那么该忠诚度$S(k)=p$。然而,事实上,我们可以定义已经使用了该产品$k$次的用户个数为$u_k$,那么实际上的忠诚度为$S(k)=\frac{u_{k+1}}{u_k}$。该“忠诚度”实际计算出来的曲线很可能是一个单调递增的凹函数(近似),如下图。
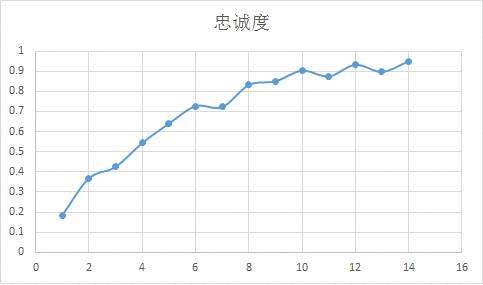
这意味着,随着用户使用该产品次数的增加,用户的忠诚度也在增加。如果你在分析自己产品的用户使用和流失的情况,或者搞营销,说不定可以有所帮助哦:-)










 京公网安备 11010802041100号
京公网安备 11010802041100号