向量学习之高维思考

前两年看了一部电影叫《星际穿越》，电影的最后有个精彩的桥段，是男主跌落到了宇宙中的黑洞深处。他发现自己进入了一个高维空间。他能够看到他在地球上的女儿，他女儿看不见他。而且能看到不同时空状态下他的女儿。比如昨天的，现在的和明天的女儿。当时就觉得编剧脑洞真大，可最近两年大家总在说高维思考，理论不好理解，但是这部电影其实很好的诠释了高维的概念，三维大家都知道，第四维其实就是时间，看似完全没有联系的内容就通过一个新的概念联系在了一起，就好像最近我们在学习的向量，里面有很多的数学概念，因为断断续续的学习，其实有些内容掌握的不是很好，对于今天这篇文章来说，概念性的理解并不是很透彻，但是我感觉学习向量的目的不光是为了学习数学而学习，更多的是提升自己高维思考的能力，所以我也想从这个角度来深入的来说一下自己的理解。

可能大家都听过一句话叫“于一滴水中见三千大千世界”。这句话什么意思不去探讨，只说这里面有关于多维思考的隐射，你看到的仅仅只是一滴水，但是在别人眼里却是五彩斑斓，丰富多彩的大千世界，我们最常听到的就是仁者见仁智者见智，现在人与人之间的维度思考差异正在拉大。你看不到的东西不代表别人看不到。我们现在面临的竞争问题已经不仅仅只是知识的储备，学历的差距，工作的经验。最终你不如别人的地方可能正是思考维度的层次不同，不能升维思考的一个原因源于我们抽象思维能力的欠缺。思维太过具象的人，会盯着事物所呈现出的表象琢磨，而抽象思维能力高的人会突破事物的表象，回到事物的源头和真相去琢磨。网上看过一些小故事，说原始社会的人对数字的理解最多能理解到“5”，多于“5”对他们来说就是无法想象了。如果你问阿基米德时代的人海滩上有多少沙子，他们会说无穷多，阿基米德时代的人无法理解“100万”这样的大数。蒙古大汗带兵打仗统计兵马的方法是，在草场上用篱笆围个大圈，让部队一批批进入这个圈，进出5次，就代表我的部队有＂5”人，我们看来可以精确把握的东西他们却把握不了。回到现代，比如:偶数和自然数哪个多，比如:直线和曲线上的点哪个多？老师同样也提出过这样的问题，记得有一节课的内容就是讨论类似的数学题，那节课老师把高维思想引入到了数学里，但是当时老师没有明说，只是要我们思考，但是的感觉就是原来还有这么一回事，是呢，为什么是这样的呢，现在再学向量，似乎当时的那层窗户纸被捅破了，也突然明白老师这个伏笔埋的真好。

其实抽象能力随着现在年龄阶段的不同，在成反比例的增长，怎么说呢，就是00后的抽象能力高出70后很多很多，这和他们的知识面见识广有很大的关系，网络的发展，带动知识的共享，信息的共享，多方面多角度的再给现在人呈现出一个问题的多角度思考，媒体在其中发挥了很大的作用，通过网络了解别人的思想，接收别人的信息，你的思想也随之在变化，有提高，有突破，有豁然开朗，有思维碰撞也有爆炸，懂得越来越多，思考的角度越来越多，但是随着年龄的增大，固有思想根深蒂固，比如很多年轻人可以轻松理解未来部分是可知的、可规划的，但不少中老年人则认为未来完全不可知不可控，因此，他们在做规划时直接少了ー个可把握维度，做事方式频繁呈现乱撞的状态。但是如果规划做的特别细致特别具象，其脆弱性也往往越强，存在度越低，因为这样的计划需要太多条件支撑，任何一个条件一变就“计划赶不上变化＂了，抽象思维不够，是无法做出长期有效的规划的。我们对世界的认知就是对世界某些关键特征的提炼，比如重力，这只是对东西往下掉这个现象的一个解释，是人编造出来可以合理解释这个现象的东西，再比如， 世界上本来没有“1”的概念，但我们却从中提炼出了“1”，“1”只是我们从事物众多特性中提炼出的一种属性，除了1外，大量的事物其它属性，比如水杯，还有颜色、大小、用途、材质、手感等等多方面的属性。再比如1+1=2，数学里成立，但是一个苹果+一个毛巾=2只猫显然是不成立的，但是，我们可以从中找出它们的共性，抽象出了1+1=2的数学概念。抽象能力就是一种高维思考的能力，只是当你拥有了高维思想后,再往下看时,就像《星际穿越》里演的那样，你会看到另外一个世界,让自己的眼界不在局限于二维三维世界，让人生之路变得更加宽阔，更多选择，让生命愈加的缤纷。拥有高维思想是为了让你在具备看事物本质、长远,透彻的情况下,能让自己在大多数时候对大多数事件做出最适合当时的选择。人与人最大的区别也正是在于思维。这里说的思维就是思考问题的方式,这跟你所学到的知识、技能或者阅历有关系,但关系并不大。

说到抽象能力自然想到自己的专业，老师一直讲代码的抽象封装，没有封装，就不会有“面向对象”的说法，而继承和多态，都是建立在封装的基础之上。抽象就是忽略一个问题中与当前目标无关的那些方面，以便更充分的注意与当前目标有关的部分，抽象不打算了解问题的全部，而是只选择其中的一个部分，而封装就是把过程和数据包围起来，对数据的访问只能通过已定义的界面。不知道放在这里说合不合适，但是我感觉学习向量也好，了解抽象封装也罢，都是为了提高我们的高维思考能力，反之来更好的学习，提高专业能力及各方面的能力。不如一个项目经理，为了图省事不去要求程序员建立长期有拓展性的抽象架构，面对新的应用场景时往往被迫要把程序完全推到重写，这样的成本代价太高。这就是没有站在高维的角度去思考长远的目标和目的。

说了半天自己对高维思想的理解，现在回到问题上来，不是专业的解答，甚至都不一定是正确的理解，权当是对目前学习到内容的一个小的回顾。

1、方向和长度相等的向量，为什么是相等的。

这要从向量的概念出发，是既有大小又有方向的量叫向量。思考向量的两个角度一个是方向一个是长度，单从一方面考虑的话都不能称之为向量，向量没有固定的位置，也就是向量可以随便移动，或者说不在同一平面的几个向量，只要方向相同，长度相等，就是相等的向量，我们可以运用平行四边形来解释这个问题，平行及角度相同，平行的两边又相等，平行四边形平行的两边方向相同，长度相等，由此解释了方向和长度相等的向量是相等的。

2、高维思考—整体考虑的学习内容有哪些。

比如面积，买房子不考虑户型，只考虑面积，面积相同价钱就相等。同样，容器的容量也是一样，无所谓容器的形状什么样子，装的溶液一样多，就说它们的容量相等。物理中这样的概念很多，比如质量，比如距离。要说到学习，整体考虑的内容就更多了，比如英语的学习，总的来说英语要学单词，学句式，学写作，学听力发音，等等，多维度学习，才能说英语学的好，单一方面只能说英语口语不错，写作不错，考试不错，但不能统一起来说英语不错，因为英语学习是一个系统的整体的全方位的学习。再比如拿出英语单词来说，除了音标学习，对意思的学习，就不单单是词典上翻译过来的字面意思，因为你不能脱离语境，脱离时间空间的改变，单词的意思也在随之做相应的改变和发展。再比如数学的学习，语文的学习，各科的学习都是从小学，甚至幼儿园开始，经过一点一滴知识的积累，才逐步加深知识的难度，所有的学习都是从整体考虑，安排各个时间段的学习内容，知识之间没有独立存在的，相互之间都有关系，所以才有了我们编制知识网的过程，才有了N+1和1+N的学习过程。学习多去尝试思考更深一层的东西，也就是所谓事物的本质。因为所有的底层的规律都是相通的。构建自己的知识体系，把各个知识点串联起来，就会发现清晰的知识体系。

3、向量的计算法则，三角形法则和四边形法则。

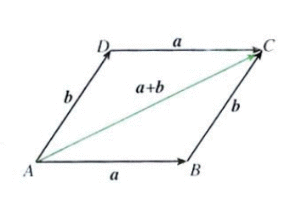
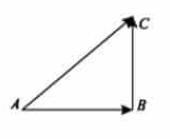
a,b两个向量相加，合就是a+b，假设a和b都是二维空间  的向量，其合就是上图中的平行四边形的对角线。三角形法则和平行四边形法则本质上是一样的,只不过三角形法则更简单,平行四边形使用更广.例如平行四边形ABCD,AB和CD是对边,向量BA+向量BC中,BC可以平移为BD,如此便是三角形法则。

4、多向量为什么只可以分解成两个正交分解。

把一个向量分解为两个互相垂直的向量，叫做把向量正交分解。这里对什么是多向量暂时不是很清楚，所以这个问题需要后面再学习一下，暂时做个留白吧。

5、有了向量的认知能力，思想是如何飞翔的。

文章前半部分就算是我思想的一个飞跃吧，飞翔还算不上，毕竟高维的翅膀也才只长出来一点点，后期还需要多加的学习，使用来丰盈羽翼。