现代信号处理——自适应滤波器（卡尔曼滤波）

一、Kalman滤波的过程方程和观测方程

假设某系统n时刻的状态变量为x(n)

过程方程：x(n+1)=F(n+1，n)x(n)+v1(n)

观测方程：y(n)=C(n)x(n)+v2(n) 

F(n+1,n)为状态转移矩阵；

C(n)为观测矩阵；

x(n)为状态向量；

y(n)为观测向量；

v1为过程噪声；v2为观测噪声。

 二、新息过程（新的信息）

 三、Kalman的递推算法

 ​​​​​​​

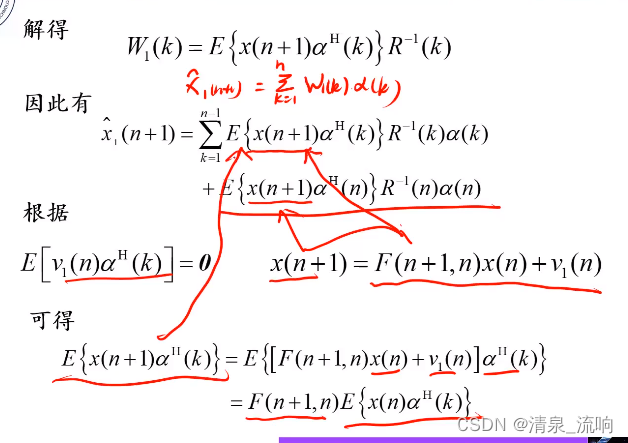
 Kalman滤波算法流程：

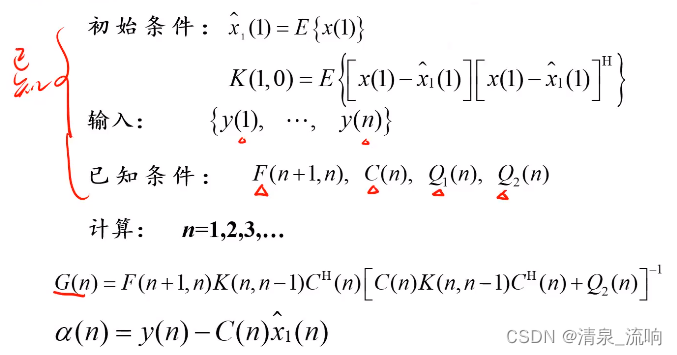
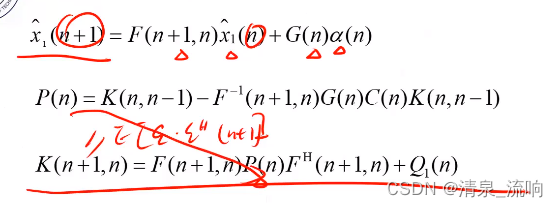
Kalman滤波的特点：

Kalman滤波采用物理意义较为直观的时间域描述方式；

采用递推算法，用前一个估计值和最近一个观察数据(它不需要全部过去的观察数据)来估计信号的当前值；

解是以估计值(常常是状态变量值)形式给出的，或者说其信号模型是从状态方程和量测方程得到的；

适用于多维和非平稳随机信号。

例：用如下差分方程产生一个AR(2)随机序列。

x(n)=1.74x(n-1)-0.81x(n-2)+v(n)，x(-1)=x(0)=0

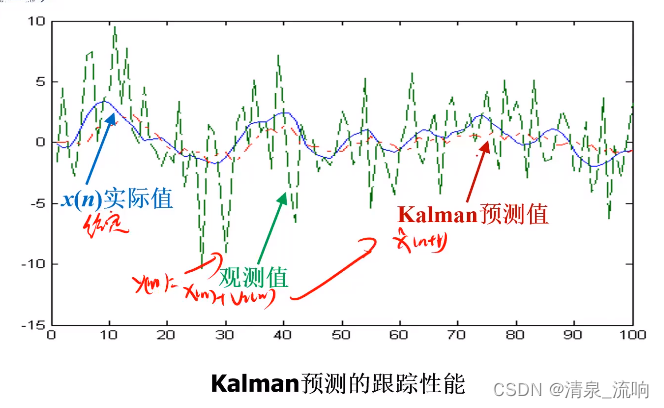
用观测方程y(n)=x(n)+v2(n)观测x(n)，其中v(n)，v2(n)分别是方差为0.04和9的白噪声，利用Kalman预测对x(n)进行预测。

Kalman预测的参数为： 

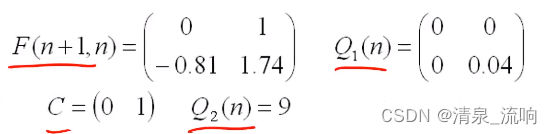
实验的方法是：由

x(n)=1.74x(n-1)-0.81x(n-2)+v(n)， x(-1)=x(0)=0产生随机序列的一次实现x(n)，

利用y(n)=x(n)+v2(n)作为观测数据得到预测值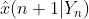，比较预测值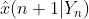和真实值x(n+1)，评价Kalman预测的跟踪性能。

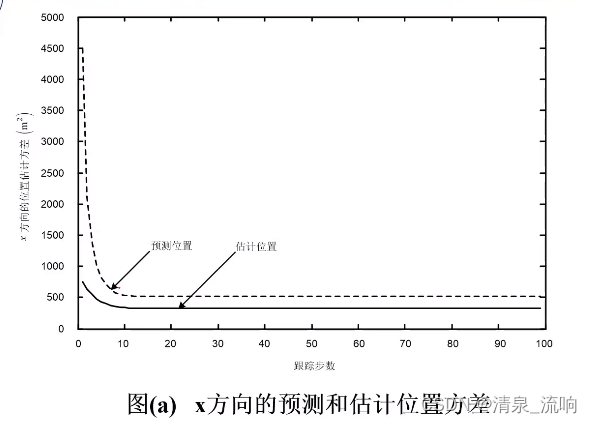
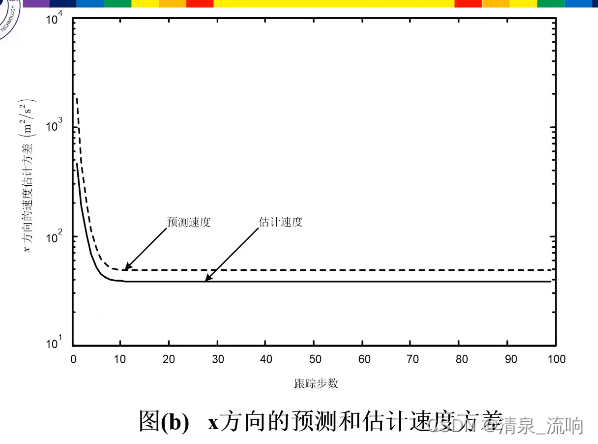
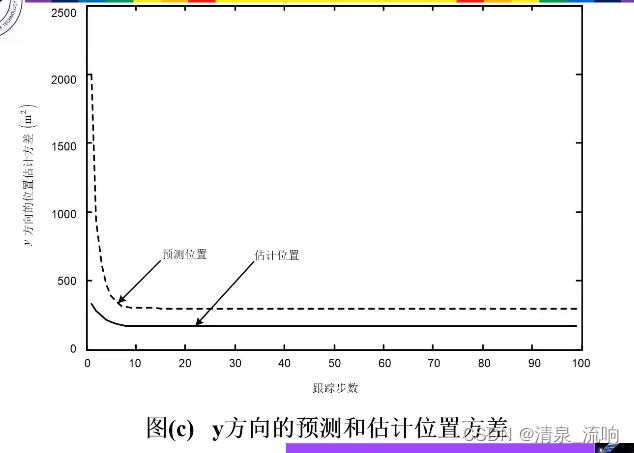
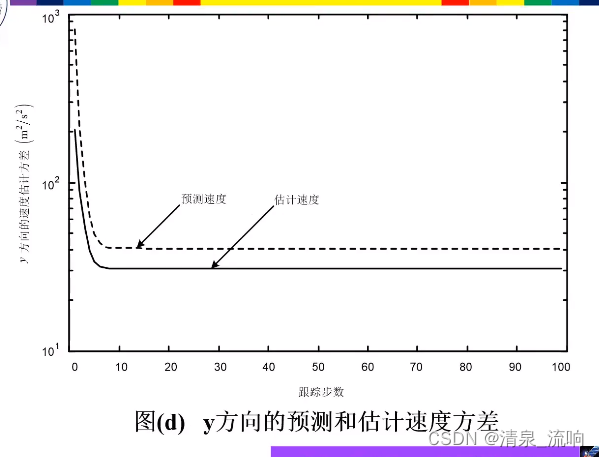
卡尔曼滤波在雷达目标跟踪中的应用

当卡尔曼滤波应用于目标跟踪时，用系统状态方程来描述目标的运动特性：

状态向量通常由目标的位置、速度和（或）加速度参量构成；

观测方程中的观测向量则由雷达测得的目标运动参量构成。 

对于匀速直线运动目标，在没有任何扰动的情况下，满足 

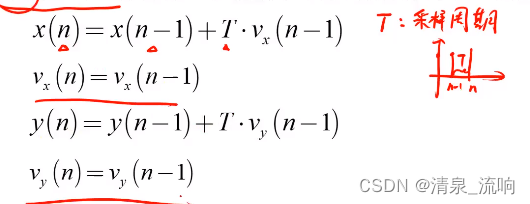
在给定系统状态方程和观测方程下，为进行卡尔曼滤波，需给出状态估计和估计误差自相关矩阵的初始值，下面给出目标跟踪时，工程上常用的状态向量估计初始化方法。 

参考视频：

https://www.bilibili.com/video/BV1wS4y1D7ng?p=9&vd_source=77c874a500ef21df351103560dada737