文本预处理，语言模型，循环神经网络

序列长度增加，计算和存储多个词共同出现的概率的复杂度会呈指数级增加。$n$n元语法通过马尔可夫假设简化模型，马尔科夫假设是指一个词的出现只与前面$n$n个词相关，即$n$n阶马尔可夫链（Markov chain of order $n$n），如果$n=1$n=1，那么有$P(w_3 \mid w_1, w_2) = P(w_3 \mid w_2)$P(w3​∣w1​,w2​)=P(w3​∣w2​)。基于$n-1$n−1阶马尔可夫链，我们可以将语言模型改写为

$P(w_1, w_2, \ldots, w_T) = \prod_{t=1}^T P(w_t \mid w_{t-(n-1)}, \ldots, w_{t-1}) .$P(w1​,w2​,…,wT​)=t=1∏T​P(wt​∣wt−(n−1)​,…,wt−1​).

以上也叫$n$n元语法（$n$n-grams），它是基于$n - 1$n−1阶马尔可夫链的概率语言模型。例如，当$n=2$n=2时，含有4个词的文本序列的概率就可以改写为：

$$

\begin{align*}
P(w_1, w_2, w_3, w_4)
&= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_1, w_2, w_3)\
&= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_2) P(w_4 \mid w_3)
\end{align*}

$$

当$n$n分别为1、2和3时，我们将其分别称作一元语法（unigram）、二元语法（bigram）和三元语法（trigram）。例如，长度为4的序列$w_1, w_2, w_3, w_4$w1​,w2​,w3​,w4​在一元语法、二元语法和三元语法中的概率分别为

$$

\begin{aligned}
P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2) P(w_3) P(w_4) ,\
P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_2) P(w_4 \mid w_3) ,\
P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_2, w_3) .
\end{aligned}

$$

当$n$n较小时，$n$n元语法往往并不准确。例如，在一元语法中，由三个词组成的句子“你走先”和“你先走”的概率是一样的。然而，当$n$n较大时，$n$n元语法需要计算并存储大量的词频和多词相邻频率。
3.循环神经网络
本节介绍循环神经网络，下图展示了如何基于循环神经网络实现语言模型。我们的目的是基于当前的输入与过去的输入序列，预测序列的下一个字符。循环神经网络引入一个隐藏变量$H$H，用$H_{t}$Ht​表示$H$H在时间步$t$t的值。$H_{t}$Ht​的计算基于$X_{t}$Xt​和$H_{t-1}$Ht−1​，可以认为$H_{t}$Ht​记录了到当前字符为止的序列信息，利用$H_{t}$Ht​对序列的下一个字符进行预测。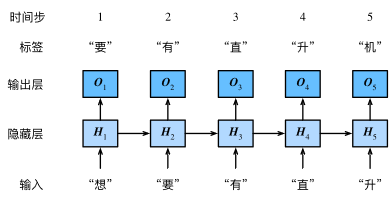

我们先看循环神经网络的具体构造。假设${\mathit{X}}_t\in {\mathbb{R}}^{n\times d}$Xt​∈Rn×d是时间步$t$t的小批量输入，$\boldsymbol{H}_t \in \mathbb{R}^{n \times h}$Ht​∈Rn×h是该时间步的隐藏变量，则：

$\boldsymbol{H}_t = \phi(\boldsymbol{X}_t \boldsymbol{W}_{xh} + \boldsymbol{H}_{t-1} \boldsymbol{W}_{hh} + \boldsymbol{b}_h).$Ht​=ϕ(Xt​Wxh​+Ht−1​Whh​+bh​).

其中，$\boldsymbol{W}_{xh} \in \mathbb{R}^{d \times h}$Wxh​∈Rd×h，$\boldsymbol{W}_{hh} \in \mathbb{R}^{h \times h}$Whh​∈Rh×h，$\boldsymbol{b}_{h} \in \mathbb{R}^{1 \times h}$bh​∈R1×h，$\phi$ϕ函数是非线性**函数。由于引入了$\boldsymbol{H}_{t-1} \boldsymbol{W}_{hh}$Ht−1​Whh​，$H_{t}$Ht​能够捕捉截至当前时间步的序列的历史信息，就像是神经网络当前时间步的状态或记忆一样。由于$H_{t}$Ht​的计算基于$H_{t-1}$Ht−1​，上式的计算是循环的，使用循环计算的网络即循环神经网络（recurrent neural network）。

在时间步$t$t，输出层的输出为：

$\boldsymbol{O}_t = \boldsymbol{H}_t \boldsymbol{W}_{hq} + \boldsymbol{b}_q.$Ot​=Ht​Whq​+bq​.

其中$\boldsymbol{W}_{hq} \in \mathbb{R}^{h \times q}$Whq​∈Rh×q，$\boldsymbol{b}_q \in \mathbb{R}^{1 \times q}$bq​∈R1×q。

RNN存在的问题：梯度较容易出现衰减或爆炸（BPTT）
⻔控循环神经⽹络：捕捉时间序列中时间步距离较⼤的依赖关系
RNN:

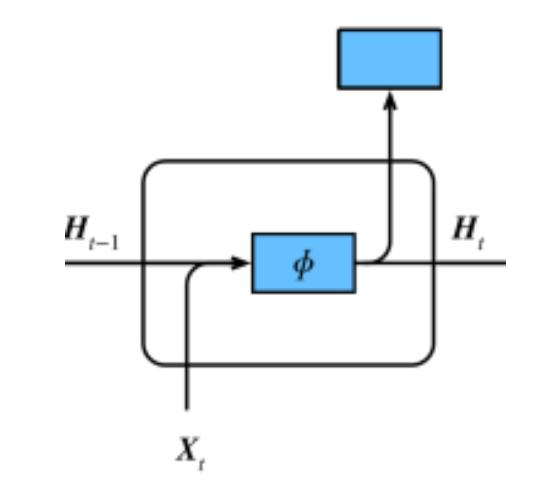
$H_{t} = ϕ(X_{t}W_{xh} + H_{t-1}W_{hh} + b_{h})$Ht​=ϕ(Xt​Wxh​+Ht−1​Whh​+bh​)
GRU:

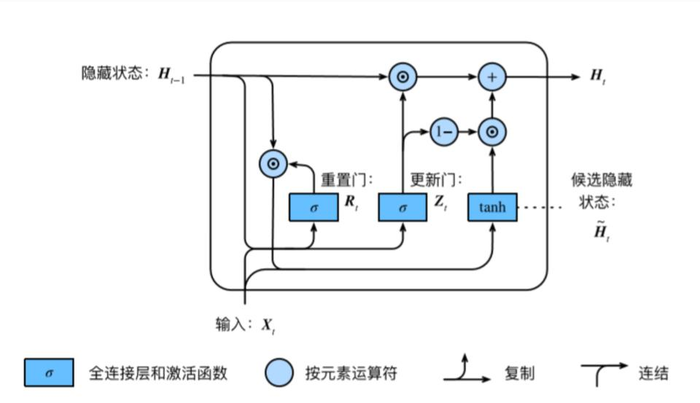
$R_{t} = σ(X_tW_{xr} + H_{t−1}W_{hr} + b_r)\\ Z_{t} = σ(X_tW_{xz} + H_{t−1}W_{hz} + b_z)\\ \widetilde{H}_t = tanh(X_tW_{xh} + (R_t ⊙H_{t−1})W_{hh} + b_h)\\ H_t = Z_t⊙H_{t−1} + (1−Z_t)⊙\widetilde{H}_t$Rt​=σ(Xt​Wxr​+Ht−1​Whr​+br​)Zt​=σ(Xt​Wxz​+Ht−1​Whz​+bz​)Ht​=tanh(Xt​Wxh​+(Rt​⊙Ht−1​)Whh​+bh​)Ht​=Zt​⊙Ht−1​+(1−Zt​)⊙Ht​
• 重置⻔有助于捕捉时间序列⾥短期的依赖关系；
• 更新⻔有助于捕捉时间序列⾥⻓期的依赖关系。