微信APP设置通过微信号搜索到我的方法

微信APP是我们在生活中经常会需要用到的一款社交软件，在这款软件中我们会用到很多功能，最基本的就是和自己的微信好友聊天了，在使用的时候也会经常用到添加微信好友的功能，我们可以通过搜索微信号来找到目标用户进行添加，而有些用户设置了不能通过微信号搜索到自己，别人就不能通过搜索微信号来添加自己为好友了，使用其他方式会比较麻烦，所以接下来小编就跟大家分享一下微信APP打开通过微信号搜索这个功能的具体操作方法吧，有需要的朋友不妨一起来看看这篇方法教程。

1.首先第一步打开手机之后，找到微信APP的图标，点击可以进入到微信APP应用界面当中。

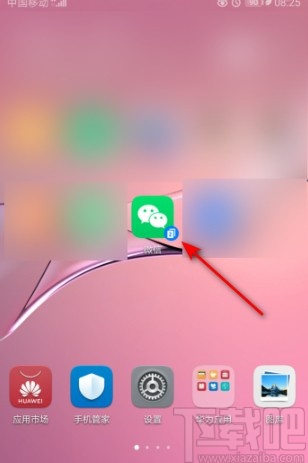
2.进入到微信界面之后，我们切换到个人中心界面，然后在个人中心界面找到设置这个功能选项，点击可以进入到设置界面中。

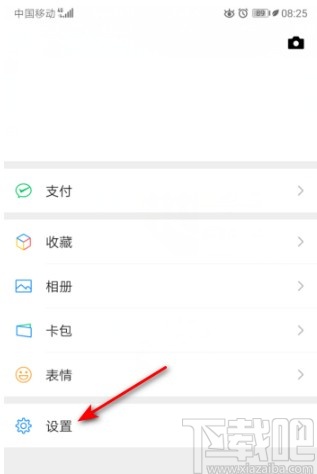
3.点击进入到应用的设置界面之后我们在设置界面中找到隐私这个设置选项，点击进入到其中。

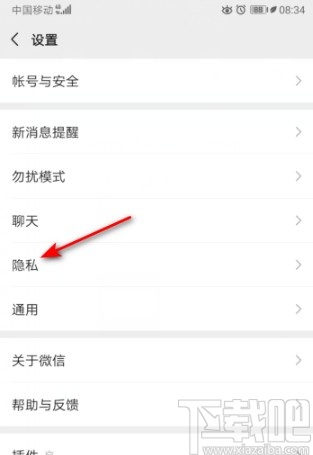
4.进入到隐私设置界面之后如下图中所示，我们在这个界面中可以找到“添加我的方式”这个选项，找到之后点击进去。

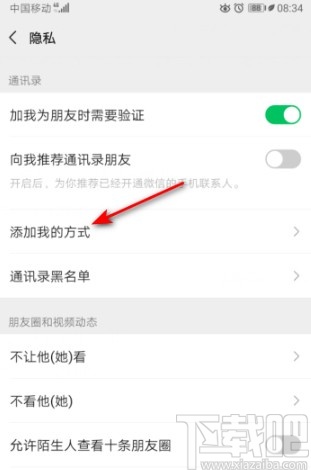
5.点击进入到添加我的方式这个界面之后，找到“微信号”这个添加方式，然后点击右边的开关将这个功能给打开即可。

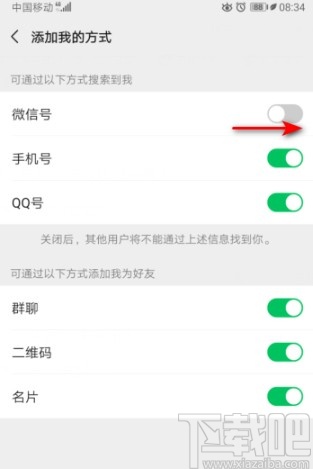
以上就是小编今天跟大家分享的使用微信APP的时候开启允许通过微信号添加我为好友的操作方法了，有需要的朋友赶紧试一试这个方法吧，希望这篇教程能帮到大家。