为什么L1正则化会有稀疏性？为什么L1正则化能进行内置特征选择？

# 个人认为&＃xff0c;这两个应该是同一个问题。

首先给大家推荐一个比较直观地搞懂L1和L2正则化的思考&＃xff0c;有视频有图像&＃xff0c;手动赞&＃xff01;

https://zhuanlan.zhihu.com/p/25707761

当然也推荐看看https://www.cnblogs.com/jclian91/p/9824310.html

回到问题&＃xff0c;为什么L1正则化会有稀疏性&＃xff1f;先盗个图。

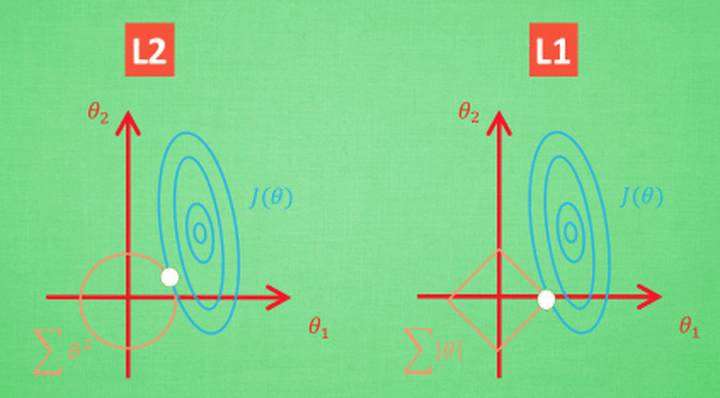
看右边那个图&＃xff0c;可以发现L1正则化的黄色部分&＃xff0c;其第一象限的斜率是固定的。要使得J(θ)在坐标轴之外的地方和L1正则化的框框相交&＃xff0c;只有在J(θ)的长轴的斜率是-1的时候(为了方便说明&＃xff0c;把J(θ)图像看做一个椭圆&＃xff0c;可能只有两个参数的时候就是一个椭圆)。

不难发现&＃xff0c;J(θ)的长轴的斜率是-1的情况是很少的&＃xff0c;所以极大概率情况下他们的交点会存在于坐标轴上。对应有图也就是只有θ1发生做了作用。

说明&＃xff1a;图中的情况虽然是为了说明&＃xff0c;但并非特殊情况&＃xff0c;其实黄色线条和蓝色线条相对位置绝大多是时候都是类似的。1、排除初始化为0的情况外&＃xff0c;θ1和θ2不可能都为0&＃xff1b;2、上面的那一段&＃xff0c;长轴斜率是-1的概率很小。

在高维特征时&＃xff0c;总之就是会出现很多正交来正交去的情况。可能出现上述链接中的例子&＃xff1a;假设模型有100个系数&＃xff0c;但是仅仅只有其中的10个是非零的&＃xff0c;这实际上是说“其余的90个系数在预测目标值时都是无用的”。这10个特征就是我们所需要选择的特征。