USACO2018openBronze试题

The cows have recently become fascinated by the game of tic-tac-toe, but since they don&＃39;t like the fact that only two cows can play at a time, they have invented a variant where multiple cows can play at once! Just like with regular tic-tac-toe, the game is played on a 3×3 3×3 board, only instead of just Xs and Os, each square is marked with a single character in the range A…Z A…Z to indicate the initial of the cow who claims that square.

An example of a gameboard might be:

COW
XXO
ABC

The cows fill in each of the nine squares before they become confused about how to figure out who has won the game. Clearly, just like with regular tic-tac-toe, if any single cow has claimed an entire row, column, or diagonal, that cow could claim victory by herself. However, since the cows think this might not be likely given the larger number of players, they decide to allow cows to form teams of two, where a team of two cows can claim victory if any row, column, or diagonal consists only of characters belonging to the two cows on the team, and moreover if characters from both cows (not just one) are used in this row, column, or diagonal.

Please help the cows figure out how many individuals or two-cow teams can claim victory. Note that the same square on the game board might possibly be usable in several different claims to victory.

SAMPLE INPUT:

COW
XXO
ABC

SAMPLE OUTPUT:

0
2

In this example, no single cow can claim victory. However, if cows C and X team up, they can win via the C-X-C diagonal. Also, if cows X and O team up, they can win via the middle row.

Problem credits: Brian Dean 

Analysis mode

Farmer John&＃39;s N N cows (2≤N≤100 2≤N≤100), conveniently numbered 1…N 1…N as always, happen to have too much time on their hooves. As a result, they have worked out a complex social structure related to the order in which Farmer John milks them every morning. After weeks of study, Farmer John has discovered that this structure is based on two key properties.

First, due to the cows&＃39; social hierarchy, some cows insist on being milked before other cows, based on the social status level of each cow. For example, if cow 3 has the highest status, cow 2 has average status, and cow 5 has low status, then cow 3 would need to be milked earliest, followed later by cow 2 and finally by cow 5.

Second, some cows only allow themselves to be milked at a certain position within the ordering. For example, cow 4 might insist on being milked second among all the cows.

Luckily, Farmer John will always be able to milk his cows in an order satisfying all of these conditions.

Unfortunately, cow 1 has recently fallen ill, so Farmer John wants to milk this cow as early in the order as possible so that she can return to the barn and get some much-needed rest. Please help Farmer John determine the earliest position cow 1 can appear in the milking order.

INPUT FORMAT (file milkorder.in):

The first line contains N N, M M (1≤M<N 1≤M), and K K (1≤K<N 1≤K), indicating that Farmer John has N N cows, M M of his cows have arranged themselves into a social hierarchy, and K K of his cows demand that they be milked in a specific position in the order. The next line contains M M distinct integers m i  mi (1≤m i ≤N 1≤mi≤N). The cows present on this line must be milked in the same order in which they appear in this line. The next K K lines contain two integers c i  ci (1≤c i ≤N 1≤ci≤N) and p i  pi (1≤p i ≤N 1≤pi≤N), indicating that cow c i  ci must be milked in position p i  pi.

It is guaranteed that under these constraints, Farmer John will be able to construct a valid milking order.

OUTPUT FORMAT (file milkorder.out):

Please output the earliest position cow 1 can take in the milking order.

SAMPLE INPUT:

6 3 2
4 5 6
5 3
3 1

SAMPLE OUTPUT:

4

In this example, Farmer John has six cows, with cow 1 being sick. He needs to milk cow 4 before cow 5 and cow 5 before cow 6. Moreover, Farmer John has to milk cow 3 first and cow 5 third.

FJ has to milk cow 3 first, and since cow 4 has to come before cow 5, cow 4 must be milked second, and cow 5 third. Thus, cow 1 can be fourth at earliest in the order.

Problem credits: Jay Leeds 

USACO 2018 US Open Contest, Bronze

Problem 3. Family Tree

Return to Problem List
Contest has ended.

Analysis mode

English (en)Armenian (hy)French (fr)Russian (ru)Spanish (es)Chinese (zh)

Farmer John owns a family-run farm that has been passed down over several generations, with a herd of cows whose familial roots can similarly be traced back several generations on the same farm. By examining old records, Farmer John is curious how the cows in his current herd are related to each-other. Please help him in this endeavor!

INPUT FORMAT (file family.in):

The first line of input contains N N (1≤N≤100 1≤N≤100) followed by the names of two cows. Cow names are each strings of at most 10 uppercase letters (A…Z A…Z). Farmer John is curious about the relationship between the two cows on this line of input.

The next N N lines each contain two cow names X X and Y Y, indicating that X X is the mother of Y Y.

OUTPUT FORMAT (file family.out):

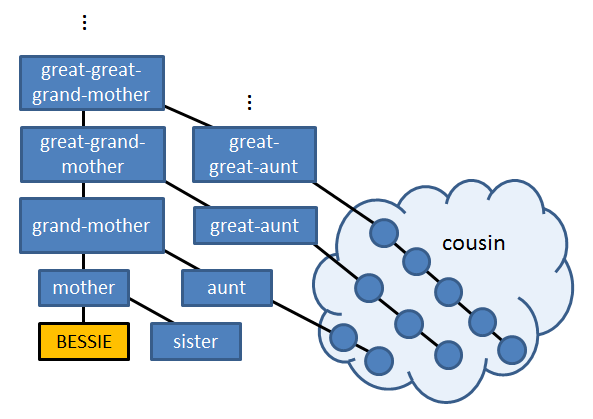
You should print one line of output indicating the relationship between the two cows specified on the first line of input (for simplicity, let&＃39;s call these two cows BESSIE and ELSIE for the examples below). Here are the different types of relationships that are possible:

• You should output "SIBLINGS" if BESSIE and ELSIE have the same mother.
• BESSIE might be a direct descendant of ELSIE, meaning that ELSIE is either the mother, grand-mother, great-grand-mother, great-great-grand-mother, etc., of BESSIE. If this is the case, you should print "ELSIE is the (relation) of BESSIE", where (relation) is the appropriate relationship, for example "great-great-grand-mother".
• If ELSIE is a child of an ancestor of BESSIE (and ELSIE is not herself an ancestor or sister of BESSIE), then ELSIE is BESSIE&＃39;s aunt. You should output "ELSIE is the aunt of BESSIE" if ELSIE is a child of BESSIE&＃39;s grand-mother, "ELSIE is the great-aunt of BESSIE" if ELSIE is a child of BESSIE&＃39;s great-grand-mother, "ELSIE is the great-great-aunt of BESSIE" if ELSIE is a child of BESSIE&＃39;s great-great-grand-mother, and so on.
• If BESSIE and ELSIE are related by any other means (i.e., if they share a common ancestor), they are cousins, and you should simply output "COUSINS".
• You should output "NOT RELATED" if BESSIE and ELSIE have no common ancestor, or neither is directly descended from the other.

The following diagram helps illustrate the relationships above, which are the only relationship types you need to consider. Observe that some relationships like "niece" (daughter of sister) are not necessary since if BESSIE is the niece of ELSIE, then ELSIE is BESSIE&＃39;s aunt.

SAMPLE INPUT:

7 AA BB
MOTHER AA
GGMOTHER BB
MOTHER SISTER
GMOTHER MOTHER
GMOTHER AUNT
AUNT COUSIN
GGMOTHER GMOTHER

SAMPLE OUTPUT:

BB is the great-aunt of AA

Problem credits: Brian Dean