基于MATLAB的TDOA定位：Chan算法与Taylor算法对比仿真

最近在研究TDOA定位技术，特别是Chan算法和Taylor算法的性能对比。这两种算法在多基站定位系统中应用广泛，各有优势。为了更好地理解它们的差异，我使用MATLAB进行了详细的仿真。

以下是两种算法的仿真效果图：

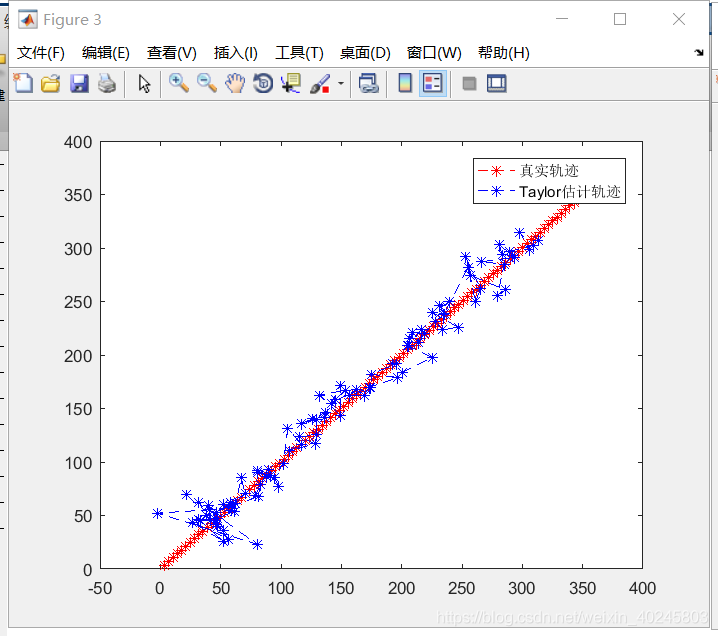
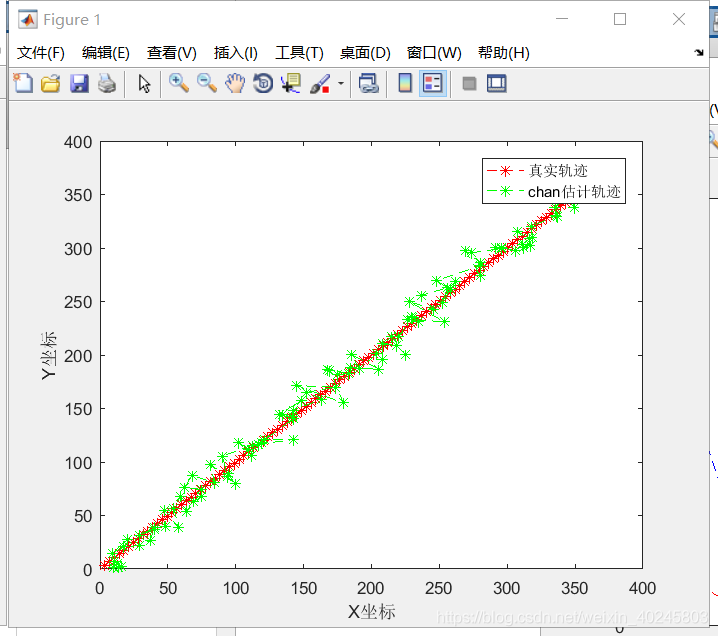
在仿真中，假设运动目标从原点出发，沿x=y方向做匀速运动。观测站的坐标如下所示：

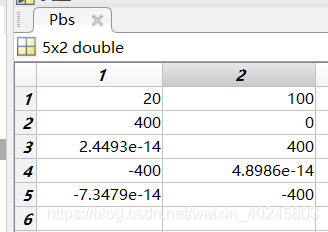
在不同的雷达测距误差下，两种算法的定位误差如下图所示：

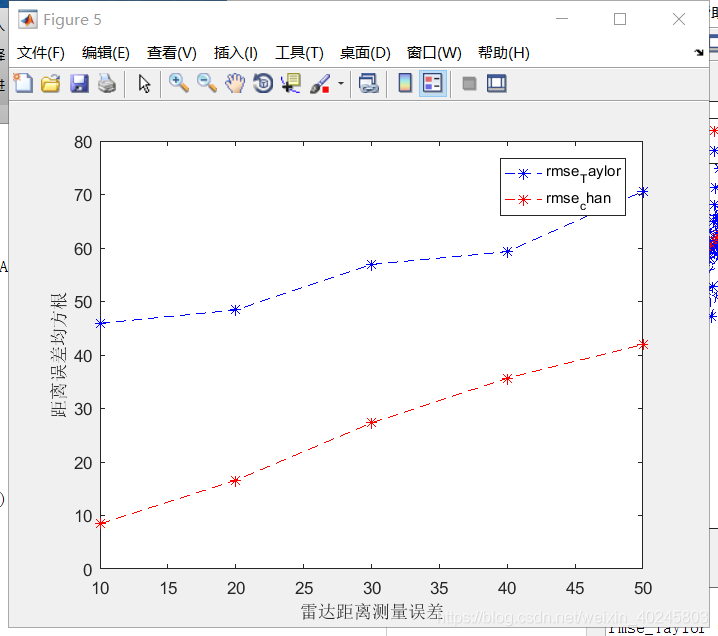
需要注意的是，Taylor算法的初值选择非常关键。在仿真中，直接使用真实值作为初值，这在实际应用中是不可行的。建议使用第一次最小二乘法（LS）或加权最小二乘法（WLS）的定位结果作为初值，以更贴近实际情况。

通过仿真，可以明显看出两种算法的差异。需要源码的同学可以在我的主页下载。

感谢Iam_Flash的提问，关于chan算法的改进，建议在第二次WLS定位中选择位置。由于参考基站的位置会影响第二次WLS的求解结果，建议将参考基站设置为（0，0），确保待测目标出现在第一象限内，避免出现虚数解。如果出现虚数解，可以通过特定方法进行处理，恢复出估计值。

未修改参考基站坐标时，直接更改chan算法的位置参数，可能会导致如下情况：

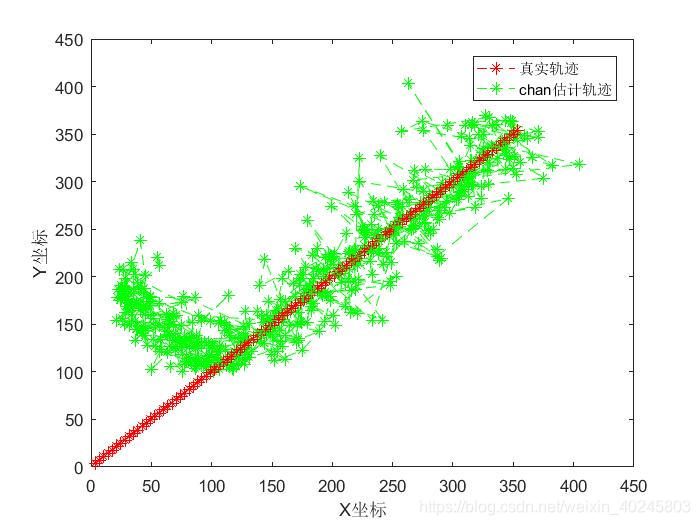
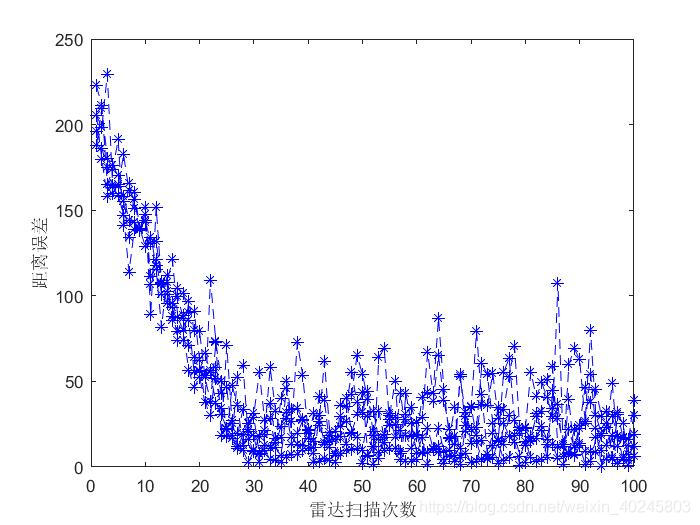
虚数解被滤除。修改参考基站坐标后，将参考基站坐标改为（-100，-100），重新输出结果如下：

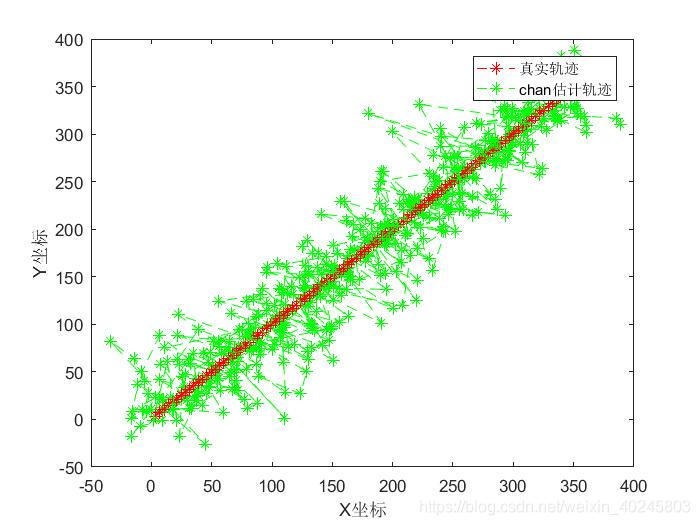
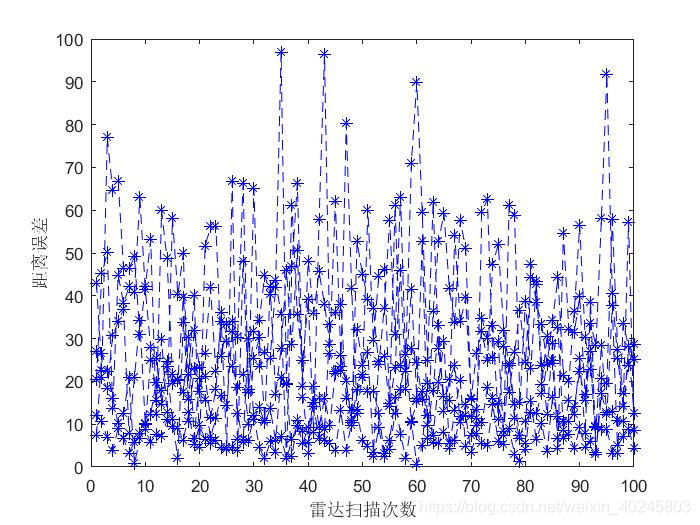
function [rmse_c, rmse_T] = TDOAchan_Taylor_comparise(noise)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%     设置基站信息
%  delta  TDOA测量误差的标准差,用于产生Q矩阵
%  M      参考基站外的基站数量
%  Xb = -100; Yb = -100;    %参考的基站坐标
%   c     光速
%   X     参考基站的坐标
%   T: 雷达的扫描间隔，此时设为1秒
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
delta = noise;
M = 4;
Xb = -100; Yb = -100; %参考的基站坐标
c = 3e8;
X = zeros(M, 2);
T = 1;
%生成其他基站的坐标 
a = 2 * pi / M;
for i = 1:M
     X(i, 1) = 3000 * cos(a * (i - 1));
     X(i, 2) = 3000 * sin(a * (i - 1));
end