数据库系统概论专门关系运算除运算

上一周学了除运算，书上的定义乍一看完全懵，必须要好好分析一下才能理解。本弱鸡正在进步，下面就来分享一下自己的见解。如果发现错误，请指出。

先看书上除运算的定义：

我们知道关系是一张二维表，所以我们的研究对象就是两张二维表，作除运算之后还是一张二维表（即关系T）。T包含所有在R但不在S中的属性和属性的值。举个例子：


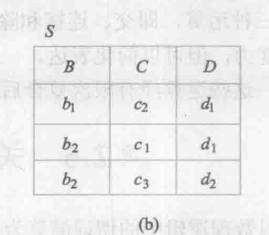
给出了R和S，按照定义，T中只包含属性A和属性A的值。A可以取{a1,a2,a3,a4}这4个值，S有3个元组，则每个值和S中的元组都有3种组合。看R中a1对应的B，C属性的值就有三种：
{(b1,c2),(b2,c3),(b2,c1)}刚好是S中的3个元组对应的B、C的值，满足“T的元组和S的元组的所有组合都在R中”。而a2,a3,a4以同样的方式就得不出这个结果。所以T=

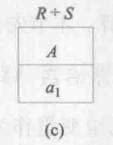
再看用象集定义的除运算：

举个例子：
给出学生选课的信息表：

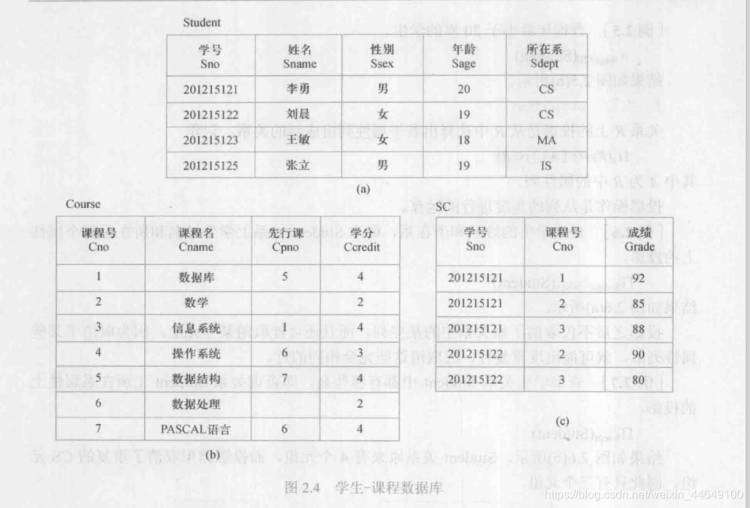
查询至少选修1号课程和3号课程的学生学号
一般的解决方法是把要解决的问题的条件“至少选修1号课程和3号课程”列成一张表，作为一个临时关系K

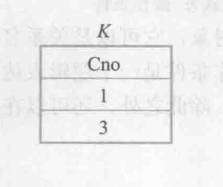
K也就是除运算的“除数”，“被除数”就是SC表，因为学号和课程号都在里面。由除运算的象集定义法，R(X,Y),S(Y,Z)在这里对应SC(学号，课程号),K(课程号，Z),Z就是其他属性组。
K在课程号（Cno）上投影的集合就是选取上图中的Cno列。
投影的概念：关系S上的投影是从S中选出若干属性列组成新的关系。这个很好理解。
“元组在X上的分量值x的象集Yx”，即表格的每一行在“学号”这个属性上都对应一个学号值x,象集Yx就是x所在的元组上的课程号的值。

求“K在课程号（Cno）上投影的集合（即课程号至少为1和3）包含在Yx里”对应的x值，就是求课程号至少包含1和3的学生的学号x。除运算的结果就是x集合，看SC表只有学号{201215121}满足条件。