作者:与爱情无关于寂寞有染_973 | 来源:互联网 | 2023-07-30 15:07
篇首语:本文由编程笔记#小编为大家整理,主要介绍了数据可视化 | 基础图表应用之散点图相关的知识,希望对你有一定的参考价值。
散点图,又名点图、散布图、X-Y图,英文Scatter plot或Scatter gram。
散点图是将所有的数据以点的形式展现在平面直角坐标系上的统计图表。它至少需要两个不同变量,一个沿x轴绘制,另一个沿y轴绘制。每个点在X、Y轴上都有一个确定的位置。众多的散点叠加后,有助于展示数据集的“整体景观”,从而帮助我们分析两个变量之间的相关性,或找出趋势和规律。此外,我们还可以添加附加的变量,来给散点分组、着色、确定透明度等等。
散点图常被用于分析变量之间的相关性。如果两个变量的散点看上去都在一条直线附近波动,则称变量之间是线性相关的;如果所有点看上去都在某条曲线(非直线)附近波动,则称此相关为非线形相关的;如果所有点在图中没有显示任何关系,则称变量间是不相关的。
如果散点图呈现出一个集中的大致趋势,这种趋势通常可以用一条光滑的曲线来近似,这样近似的过程被称为曲线拟合,而这条曲线则被称为最佳拟合线或趋势线。如果图中存在个别远离集中区域的数据点,这样的点被称为离群点或异常值。
不过,分析时需注意,相关性并不等于因果关系。例如,有统计表明,冰棒卖得越多,游泳死亡人数就越高。若是在散点图上,二者应当呈正相关,但实际上,两种现象都是由天气炎热引起的,并无直接因果关系。
图表属性
形状:散点
图类:统计图表
功能:关系 • 分布 • 趋势
图表详解
元素构成

适用场景
(1)散点图适用于分析变量之间是否存在某种关系或相关性。
如果散点图呈现出一系列随机分布的数据点,那两个变量之间可能并没有相互关系;如果大部分的数据点都相对密集地分布且呈现出某种趋势,那两个变量之间可能存在某种相关性。数据的相关关系主要分为:正相关(两个变量值同时增加)、负相关(一个变量值增加另一个变量值下降)、不相关、线性相关、指数相关、U形相关等等。
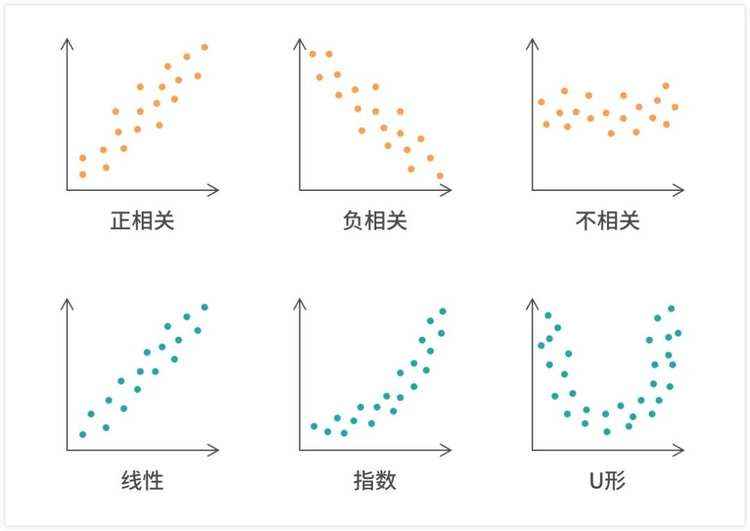
(2)散点图适用于分析变量之间相关性的强弱,我们可以通过查看图上数据点的密度来确定相关性的强弱。
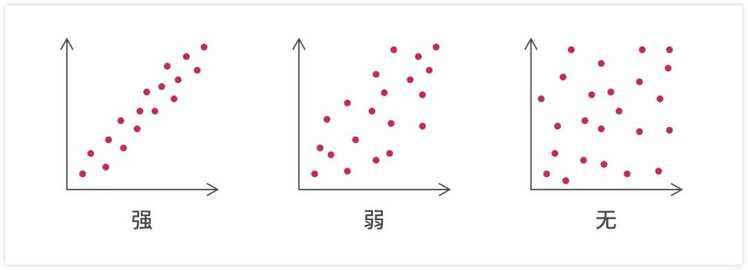
(3)散点图适用于在不考虑时间的情况下比较大量的数据点,数据点越多,比较的效果就越明显。
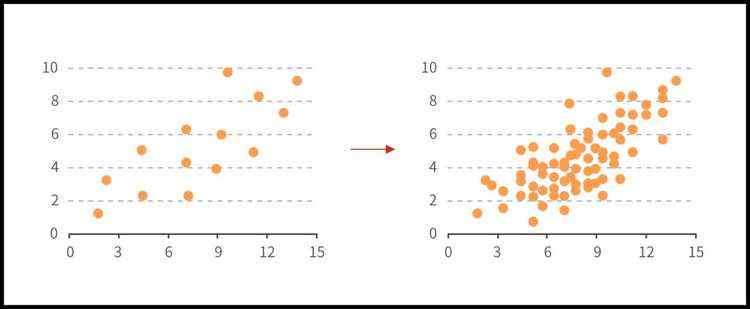
不适用场景
(1)对于数据量较少的数据集不建议使用,分析结果会存在较大的偶然性(如下图,3个点无法确定变量之间是否就是正相关)。
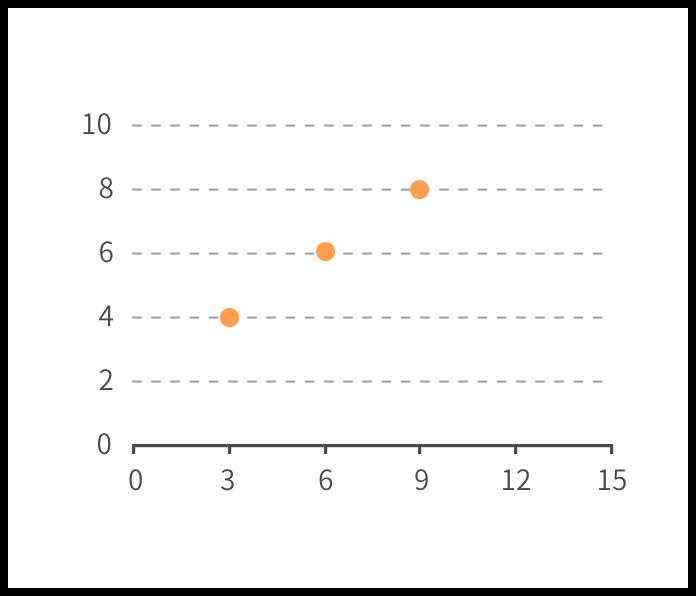
(2)不适用于数据点过大、过多的情况,会影响图表的可读性,导致无法进行分析。可以通过减小点的大小、调整透明度、减少数据量、数据分组、建立3D模型等等的方法进行优化,可参见六边形分箱图。
(3)数据分类过多,无法快速识别,失去可视化的意义和价值。
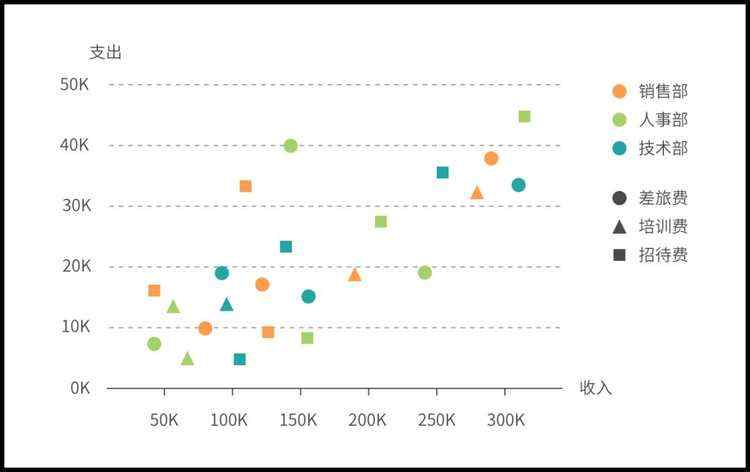
(4)通过观察散点图得出的变量之间的相关性并不等同于确定的因果关系。例如,有统计表明,冰棒卖得越多,游泳死亡人数就越高,也就是游泳死亡人数和冰棒销量之间呈正相关,但我们并不能得出“吃冰棍就会增加游泳死亡率”这样的结论。因为这两个事件都是由于夏天气温升高所致,而吃不吃冰棍和游泳死亡风险根本没有任何因果关系。
使用场景
(1)利用散点图可做相关性分析、 了解数据分布情况,如下图可分析不同来源流量与网站总流量的关系。下图展示了某公司主站的新访客各来源渠道与总新访客量。结论很直观:direct(直接访问来源)和organic(自然搜索来源)和总的新访客有明显的正相关关系(direct与newuv相关系数达到0.89,direct来源的占比达到60%)。因此,我们知道这个公司大部分访客来源于口碑,而且其潜力还相当大,因为direct和organic图显示新访客对direct的弹性比较高,没有出现像sem(蓝色)图那样的边际效益递减的情况(胡晨川, 2015)。
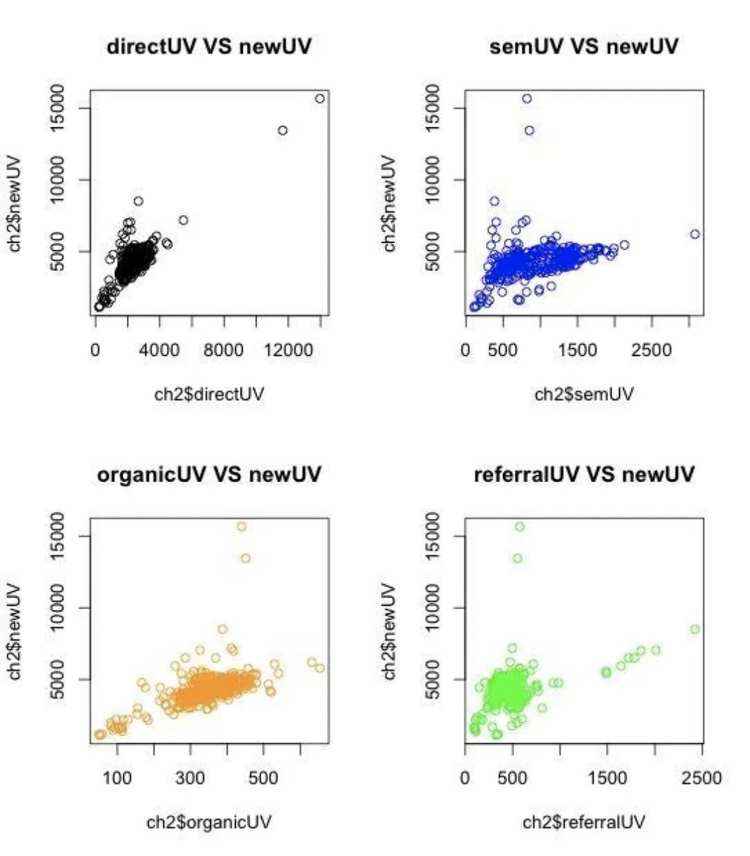
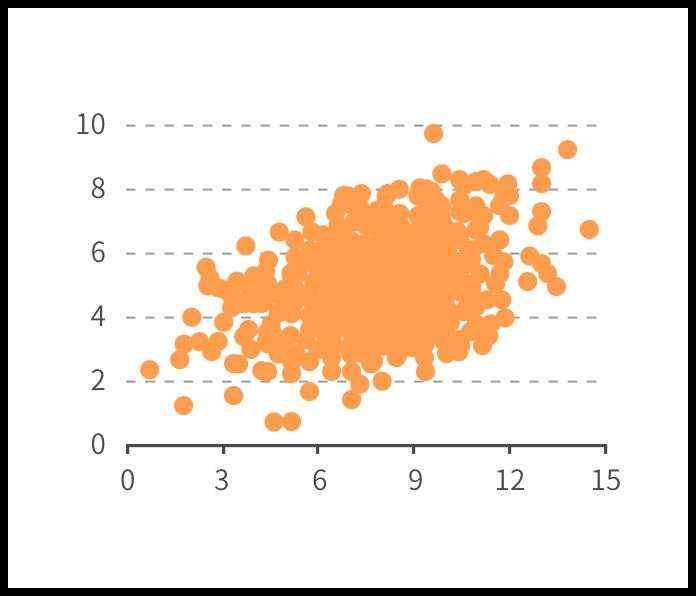
(2)散点图通常用于显示和比较数值,不光可以显示趋势,还能显示数据集群的形状,以及在数据云团中各数据点的关系。如下图(AntV墨者学院, no date)某年级所有学生身高和体重的数据可绘制成一幅散点图。从身高和体重这两个维度进行比较,我们可以看到所有的数据点比较集中,呈正相关关系,即身高越高,相应的体重会越大;且平均身高和平均体重的辅助线将散点图分为四个象限,这样我们便可以更好的看出数据的分布情况;而不同颜色的点则可以看出不同性别身高和体重数据的分布。
图片类型散点图,使用权力的游戏中的人物头像来置换数据点,很形象地表达了人物的颜值系数和性格好坏。
转载自网站:图之典。
往期推荐: