数据结构考研难点代码突破（树型查找红黑树（RBT）插入流程图，删除）

红黑树查找与删除的效率和AVL树相同。

但是因为AVL树在插入或删除节点可能破坏AVL树结构&＃xff0c;而重新调整树的开销大。所以引出了红黑树。

红黑树的插入和删除一般无需调整树的结构&＃xff0c;相比于AVL树的调整开销小。

所以&＃xff0c;在以查为核心的操作下&＃xff0c;适合使用AVL树结构&＃xff1b;如果要频繁的插入或删除元素&＃xff0c;更适合使用红黑树

红黑树定义&＃xff1a;

1. 红黑树首先是二叉排序树
2. 红黑树的每个节点有两种颜色&＃xff08;红&＃xff0c;黑色&＃xff09;
3. 树的根节点是黑色的。
4. 树的空节点都是黑色的.
5. 不存在两个相连的红节点&＃xff08;红节点的父亲与孩子都是黑色的&＃xff09;
6. 对于每一个节点来讲&＃xff0c;到任意叶节点的简单路径上&＃xff0c;黑节点个数相同

结点的黑高bh&＃xff1a;从某结点出发&＃xff08;不含该结点&＃xff09;到达任一空叶结点的路径上黑结点总数&＃xff0c;空节点算黑色。

红黑树性质&＃xff1a;

1. 从根节点到叶节点的最长路径不大于最短路径的二倍。

2. n个节点的红黑树的高度h<2log(N&＃43;1)

   红黑树高度为h&＃xff0c;根节点的黑高>h/2&＃xff0c;高度为h的红黑树节点最少为全是黑色的满二叉树。所以内部节点个数n>2^h/2-1&＃xff0c;求得h<2log(N-1)

红黑树的插入操作流程

步骤&＃xff1a;

1. 先按照搜索二叉树的插入方式进行插入新节点。

2. 如果这个节点是根节点&＃xff0c;颜色为黑色。如果节点不是根节点&＃xff0c;颜色为红色。

   • 如果插入的节点破坏了红黑树的定义&＃xff0c;调整时需要看新插入的节点的叔叔节点的颜色
   • 如果叔叔节点是黑色的&＃xff0c;需要对红黑树进行旋转&＃43;变色操作
     
     • 红黑树的旋转与AVL树的旋转相同&＃xff08;LL&＃xff0c;RR&＃xff0c;RL&＃xff0c;LR型旋转&＃xff09;
     • LL&＃xff1a;右单旋&＃xff0c;父换爷&＃43;变色
     • RR&＃xff1a;左单旋&＃xff0c;父换爷&＃43;变色
     • LR&＃xff1a;左右双旋&＃xff0c;儿换爷&＃43;变色
     • RL&＃xff1a;右左双旋&＃xff0c;儿换爷&＃43;变色
   • 如果叔叔节点是红色的&＃xff0c;需要对红黑树进行变色&＃43;变新操作
     
     • 叔父爷换色&＃xff0c;爷变为新节点

具体操作&＃xff1a;

红黑树插入&＃xff1a;20&＃xff0c;10&＃xff0c;5&＃xff0c;30&＃xff0c;40&＃xff0c;57&＃xff0c;3&＃xff0c;2&＃xff0c;4&＃xff0c;35&＃xff0c;25&＃xff0c;18&＃xff0c;22&＃xff0c;23

在红黑树插入节点只可能破坏“不存在两个相连的红节点&＃xff08;红节点的父亲与孩子都是黑色的&＃xff09;这个条件”

1. 按照搜索二叉树插入到如下图时&＃xff0c;需要调整红黑树结构&＃xff08;新插入节点5&＃xff09;
   
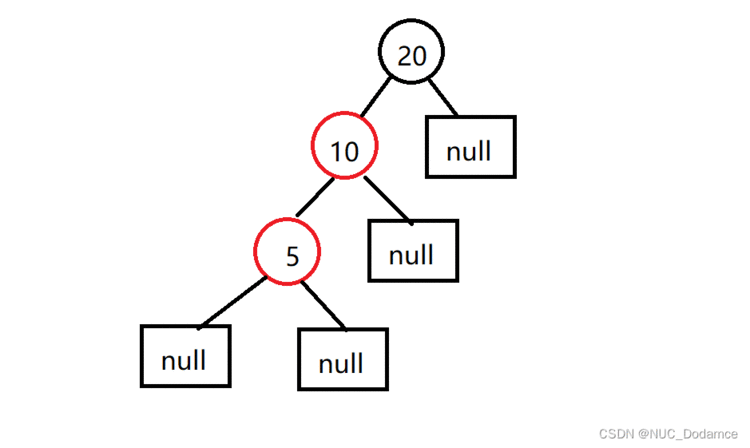
   叔叔节点是null&＃xff0c;是黑色&＃xff0c;插入的5属于LL型&＃xff0c;需要进行右单旋操作
   
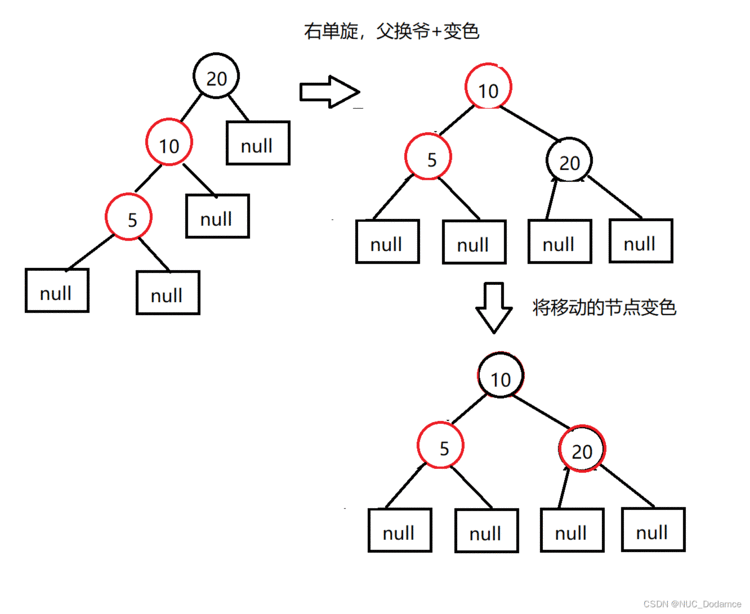
2. 之后插入30节点&＃xff0c;又不符合红黑树的定义&＃xff0c;需要进行调整
   
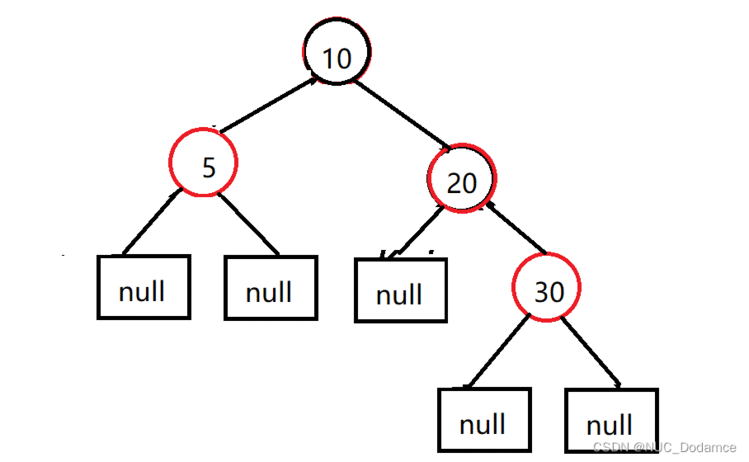
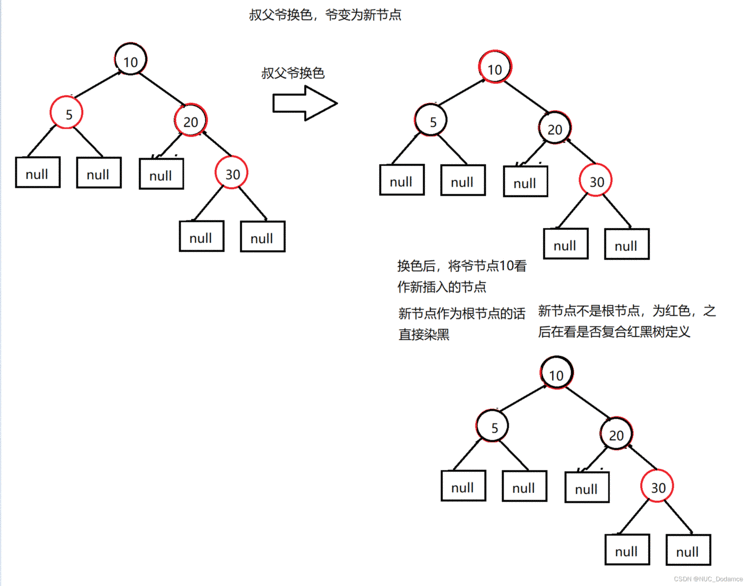
   上图新插入节点的叔叔是5节点&＃xff0c;是红色的。执行步骤 “叔父爷换色&＃xff0c;爷变为新节点”

3. 插入节点40&＃xff0c;破坏了红黑树的特性

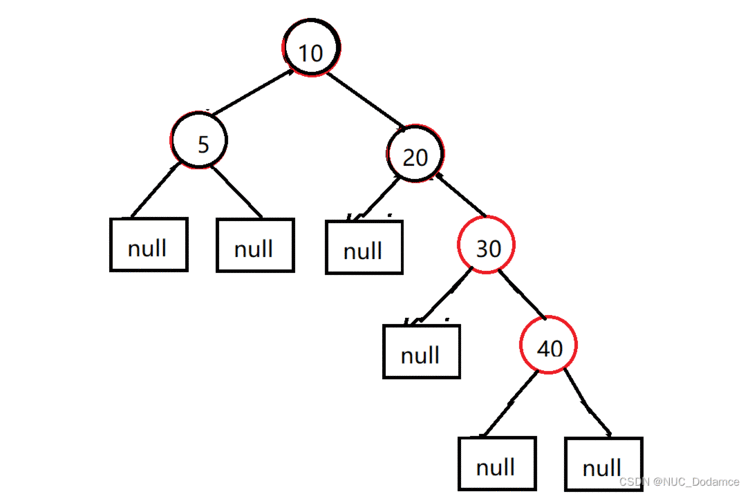
新插入的节点的叔叔是黑色的空节点&＃xff0c;插入类型是RR型

操作&＃xff1a;左单旋&＃xff0c;父换爷&＃43;变色

4. 插入57&＃xff0c;需要调整红黑树

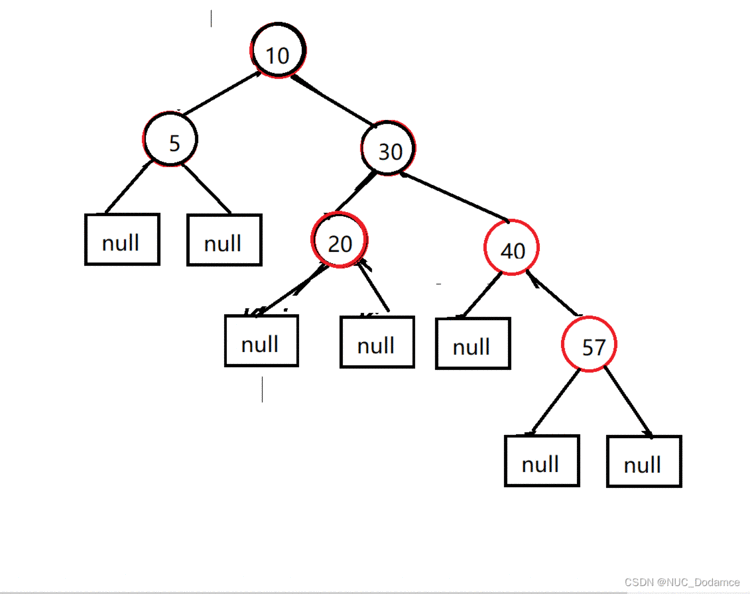
新节点叔叔20是红色的&＃xff0c;调整步骤为&＃xff1a;叔父爷换色&＃xff0c;爷变为新节点

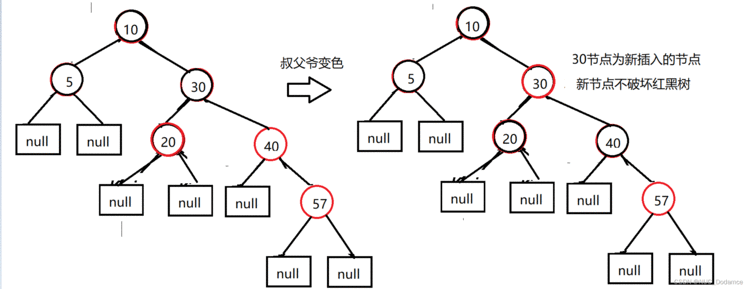
5. 插入3&＃xff0c;2节点后&＃xff0c;插入2时破坏的红黑树特性

节点2的叔叔是黑色的&＃xff0c;属于LL型&＃xff0c;右单旋&＃xff0c;父换爷&＃43;变色

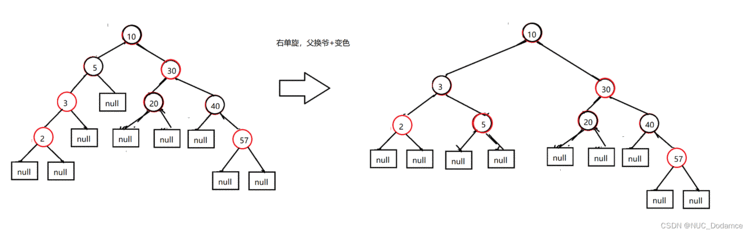
6. 插入4节点后&＃xff0c;破坏了红黑树的特性需要进行调整

插入节点4的叔叔节点是红色的&＃xff0c;叔父爷换色&＃xff0c;爷变为新节点

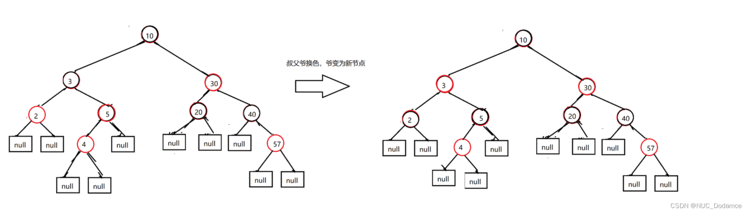
7. 插入35&＃xff0c;25节点不会改变红黑树特性&＃xff0c;插入22节点后会改变红黑树特性

22节点叔叔节点是红色的&＃xff0c;叔父爷变色后&＃xff0c;爷变成新节点

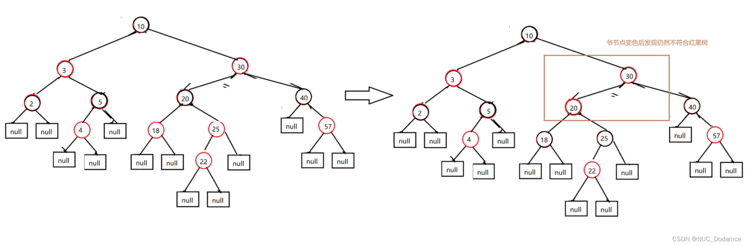
变色后发现仍然不是红黑树&＃xff0c;此时爷节点变成新节点继续调整红黑树

此时30是作为新插入节点&＃xff0c;叔叔节点是红色的&＃xff0c;叔父爷变色&＃xff0c;爷变成新节点

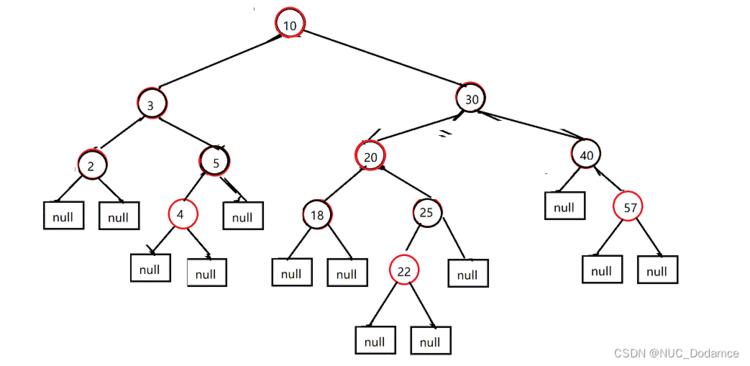
新节点变为根节点&＃xff0c;根节点变为黑色

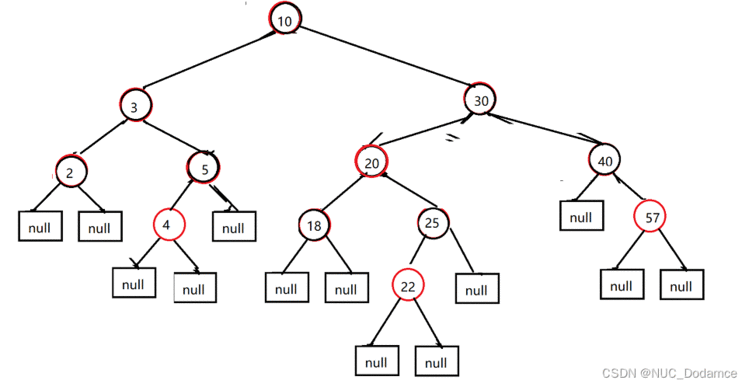
8. 插入23节点&＃xff0c;破坏了红黑树特性&＃xff0c;叔叔节点是黑色的&＃xff0c;且是LR型&＃xff0c;左右双旋&＃xff0c;儿换爷&＃43;变色(儿爷变色)

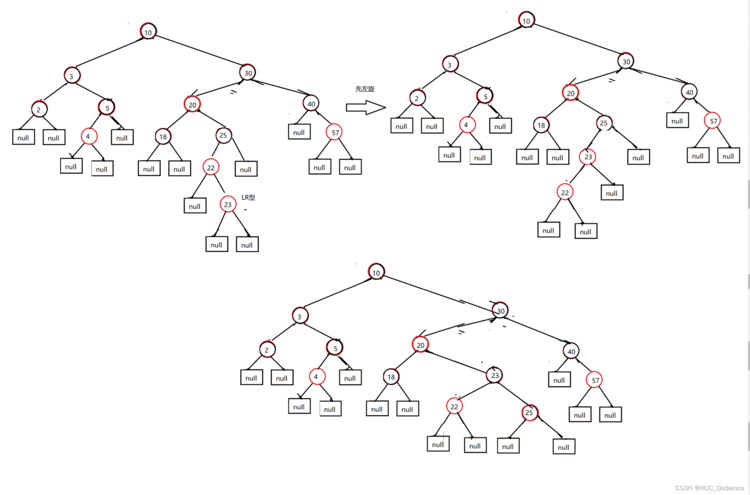
红黑树的删除&＃xff08;了解&＃xff09;

1. 红黑树删除操作的时间复杂度O(logN)
2. 红黑树中删除结点的处理方式和二叉排序树的删除一样
3. 按第二步删除结点后&＃xff0c;可能破坏“红黑树特性”&＃xff0c;此时需要调整结点颜色、位置&＃xff0c;使其再次满足“红黑树特性”。