作者:廖赞胜 | 来源:互联网 | 2023-10-14 12:45
“ 异常值是我们在数据分析中会经常遇到的一种特殊情况,所谓的异常值就是非正常数据。我们这节来讲下关于数据分析中,异常数据识别的几种算法:k-mean、箱体图法等。”
异常值是我们在数据分析中会经常遇到的一种特殊情况,所谓的异常值就是非正常数据。有的时候异常数据对我们是有用的,有的时候异常数据不仅对我们无用,反而会影响我们正常的分析结果。比如在分析银行欺诈案例时,核心就是要发现异常值,这个时候异常值对我们是有用的。再比如,在统计某个城市的平均收入的时候,有人月收入是好几个亿,这个时候这个人就是一个异常值,这个异常值会拉高城市的整体平均收入,因此可能会得到一个不真实的分析结果。
这一篇来分享下,如何识别异常值以及识别到异常值以后该如何处理。
箱体图法:
分位数识别
代表的执行方法为箱式图:
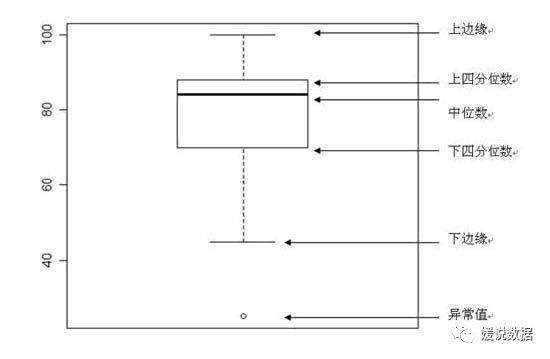
上四分位数Q3,又叫做升序数列的75%位点
下四分位数Q1,又叫做升序数列的25%位点
箱式图检验就是摘除大于Q3+3/2*(Q3-Q1)
,小于Q1-3/2*(Q3-Q1)
外的数据,并认定其为异常值;针对全量样本已知的问题比较好,缺点在于数据量庞大的时候的排序消耗
R语言中的quantile
函数,python中的percentile
函数可以直接实现。
距离识别:
最常用的就是欧式距离,
比如:两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离:

可以直观感受的到,图中,距离蓝色B点距离为基准衡量的话,红色A1,红色A2,红色A3为距离较近点,A4为距离较远的异常点。

但是这样看问题会有一个隐患,我们犯了“就点论点”的错误没有考虑到全局的问题,让我在看下面这张图:

还是刚才那张图,橙色背景为原始数据集分布,这样看来A4的位置反而比A1、A3相对更靠近基准点B,所以在存在纲量不一致且数据分布异常的情况下,可以使用马氏距离代替欧式距离判断数据是否离群。

其中,μ
为feature的均值,X
为观察值,Σ
为feature的协方差矩阵
马氏距离除了用来判断点是否异常,也可以用来判断两个数据集相识度,在图像识别,反欺诈识别中应用的也是非常普遍;问题在于太过于依赖Σ
,不同的base case对应的Σ
都是不一致的,不是很稳定
03
—
K均值聚类:
K均值聚类算法的思路非常通俗易懂,就是不断地计算各样本点与簇中心之间的距离,直到收敛为止,其具体的步骤如下:
(1)从数据中随机挑选k个样本点作为原始的簇中心。
(2)计算剩余样本与簇中心的距离,并把各样本标记为离k个簇中心最近的类别。
(3)重新计算各簇中样本点的均值,并以均值作为新的k个簇中心。
(4)不断重复(2)和(3),直到簇中心的变化趋于稳定,形成最终的k个簇。


如上图所示,图中蓝色和红色之间形成鲜明的簇,其中每个簇内包含5000个数据。如果数据中存在异常点,目测蓝色的簇可能会包含更多异常,因为数据点相对分散一些。

如上图所示,通过9个子图对Kmeans聚类过程加以说明:子图1,从原始样本中随机挑选两个数据点作为初始的簇中心,即子图中的两个五角星;子图2,将其余样本点与这两个五角星分别计算距离(距离的度量可选择欧氏距离、曼哈顿距离等),然后将每个样本点划分到离五角星最近的簇,即子图中按虚线隔开的两部分;子图3,计算两个簇内样本点的均值,得到新的簇中心,即子图中的五角星;子图4,根据新的簇中心,继续计算各样本与五角星之间的距离,得到子图5的划分结果和子图6中新的簇内样本均值;以此类推,最终得到理想的聚类效果,如子图9所示,图中的五角星即最终的簇中心点。
实现原理:
使用K均值聚类的思想识别数据中的异常点还是非常简单的,具体步骤如下:
#我是媛姐,一枚有多年大数据经验的程序媛,打过螺丝搬过砖,关注数仓,关注分析。愿你我走得更远!