神经网络学习之玻尔兹曼机

退火

　　退火是一种金属的热处理工艺&＃xff0c;将金属加热到一定的温度&＃xff0c;保持足够时间&＃xff0c;然后以适宜速度缓慢冷却。

　　退火可以改善材料性能&＃xff0c;提升金属品质。

 模拟退火算法

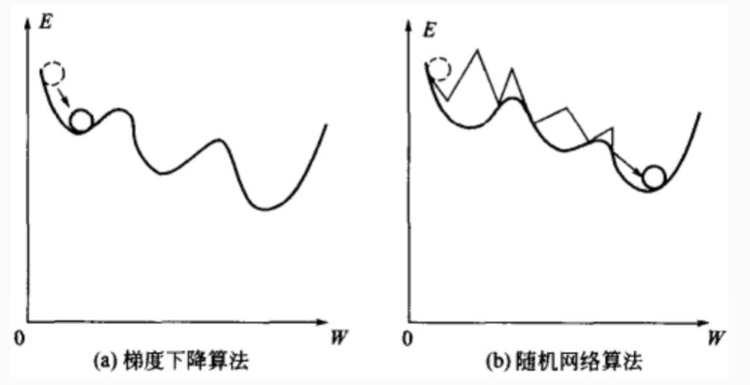
　　根据梯度下降算法考虑&＃xff0c;梯度下降算法会使得我们的代价函数的值只会往梯度下降的方向走&＃xff0c;比如左图&＃xff08;a&＃xff09;&＃xff0c;当它走到第一个凹坑里的时候它就在也出不来了。而不会到达全局的最小值&＃xff0c;会陷入局部最小值出不来。

　　模拟退火算法&＃xff0c;也叫随机网络算法&＃xff0c;如右图&＃xff08;b&＃xff09;。它和梯度下降法的能力就不一样&＃xff0c;它具有“爬坡”或“跳跃”的能力&＃xff0c;它会在局部最小值里面跳出来&＃xff0c;使损失函数的值不断下降&＃xff0c;最终达到全局最小值。

那么这是为什么呢&＃xff1f;

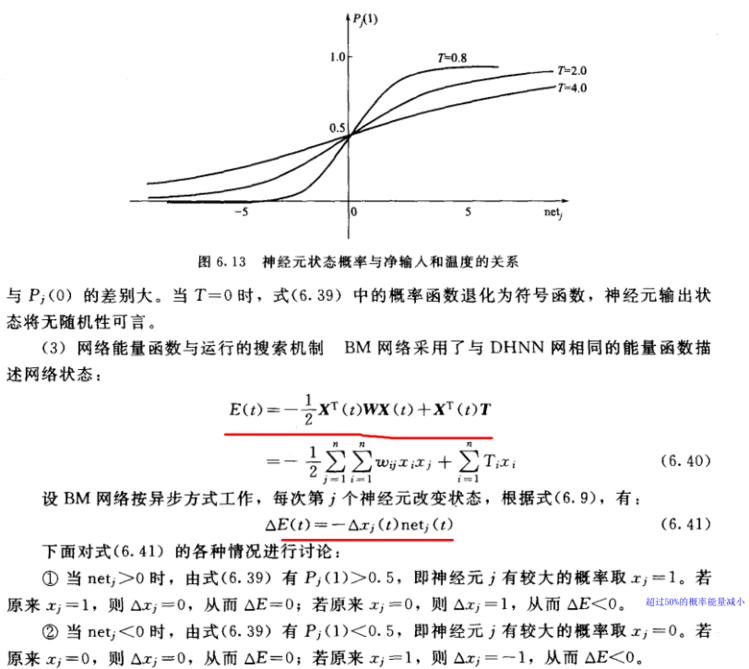
　　模拟退火算法会根据接受概率来判断要怎么走。假设前一状态为x(n)&＃xff0c;系统受到一定的扰动&＃xff0c;状态变为x(n&＃43;1)&＃xff0c;相应地&＃xff0c;系统能量由E(n)变为E(n&＃43;1)。定义系统由x(n)变为x(n&＃43;1)的接受概率为p&＃xff1a;

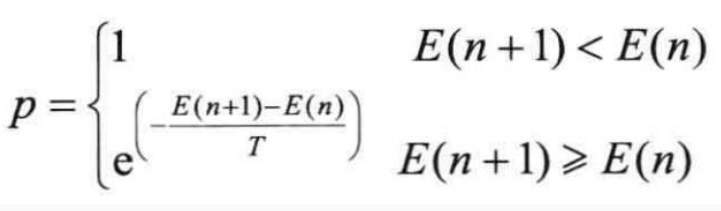
　　意思就是&＃xff0c;当损失函数从能量高的地方走向能量低的地方时&＃xff0c;其概率为1&＃xff0c;表示以一定转移。当损失函数从能量低的地方走向能量高的地方时&＃xff0c;比如从局部最小值跳出来&＃xff0c;那么就就有一定概率来判断它是否跳出&＃xff0c;这个概率就是一个能量和温度&＃xff08;T&＃xff09;之间关系的算式。

　　当T越大&＃xff0c;接收概率P就越大&＃xff0c;小球跳跃的能力就越高&＃xff0c;就更容易跳出这个局部最小值。

　　当T越小&＃xff0c;接收概率P就越小&＃xff0c;小球跳跃的能力就越低&＃xff0c;就不容易跳出这个局部最小值。

　　E&＃xff08;n&＃43;1&＃xff09;-  E&＃xff08;n&＃xff09;越大&＃xff0c;接收概率P就越小。

　　E&＃xff08;n&＃43;1&＃xff09;-  E&＃xff08;n&＃xff09;越小&＃xff0c;接收概率P就越大。

　　所以&＃xff0c;在一开始&＃xff0c;温度的初始值T要选得足够高&＃xff0c;使得所有可能的状态转移都能被接受。然后温度逐渐下降。

退火速率

　　指数下降方式&＃xff1a;T(n) &＃61; λT(0) n&＃61;1,2…&＃xff0c;λ是一个小于1的正数&＃xff0c;可以取0.8-0.99之间。

　　其他下降方式&＃xff1a;  

　　

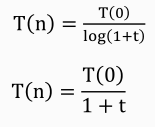
模拟退火算法过程

　　1.初始化。随机选择一定的值作为变量的数值x(0)&＃xff0c;并设置初始温度T(0)&＃xff0c;终止温度T final 和温度的下降公式。

　　2.以一定的规则&＃xff08;沿着梯度下降的方向走一段距离&＃xff0c;或者在x点附近随机取一个点&＃xff09;在当前状态x(n)附近产生新的状态x(n&＃43;1)。如果能量减小则改变状态&＃xff0c;如果能量变大则以一定的概率判断是否要改变状态。

　　3.在一定的温度T下迭代一定的次数&＃xff0c;或者判断代价函数是否趋于稳定。然后终止内循环(内循环中T不变&＃xff0c;让状态自由改变)。

　　4.调整T&＃xff0c;判断T是否是小于等于T final 。没有小于等于T final 的话&＃xff0c;则跳转到第二步继续执行。如果小于等于T final 的话&＃xff0c;则终止算法。

随机神经网络&＃xff08;玻尔兹曼机BM&＃xff09;

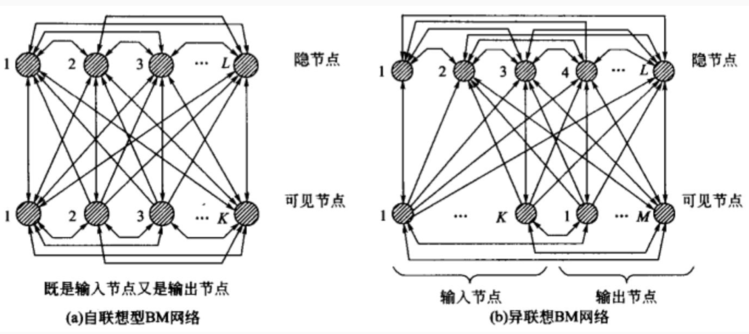
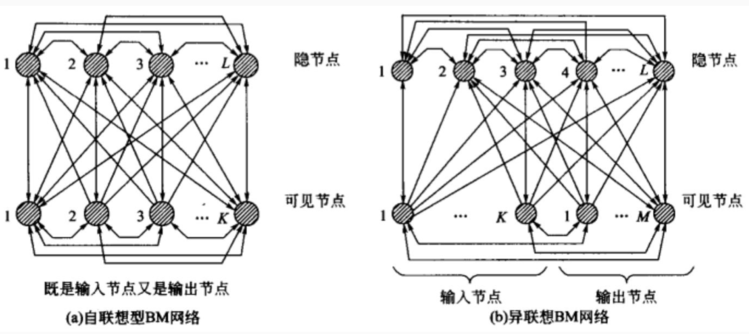
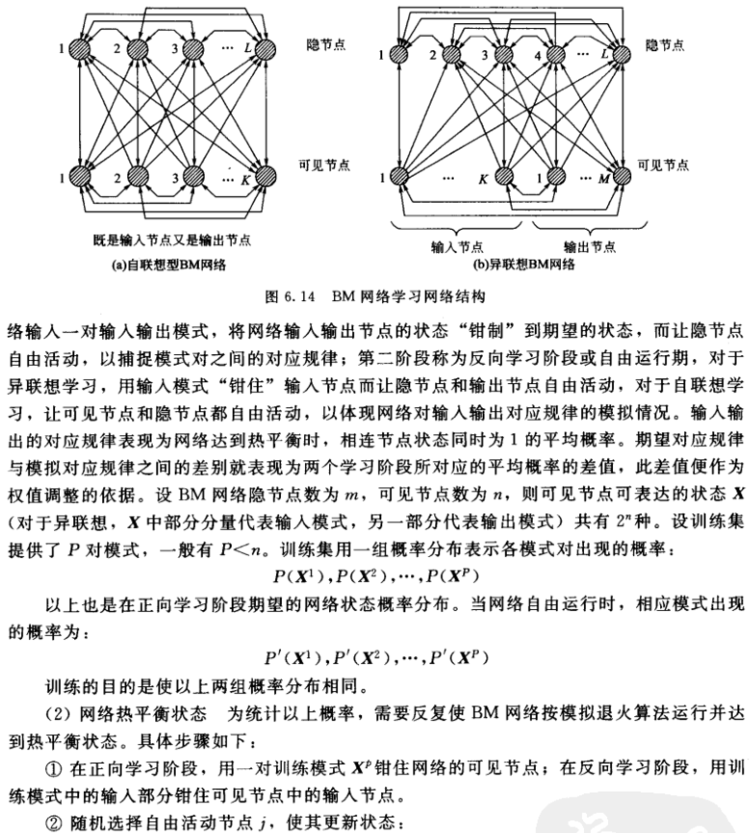
　　玻尔兹曼机分为两种&＃xff1a;&＃xff08;a&＃xff09;自联想型BM网络&＃xff0c;&＃xff08;b&＃xff09;异联想型BM网络

　　一共分为两层&＃xff0c;分为可见节点和隐节点。首先看&＃xff08;a&＃xff09;自联想型BM网络&＃xff0c;它的可见节点既是输入节点又是输出节点。当我们输入测试数据时&＃xff0c;从可见节点输入&＃xff0c;也从可见节点输出结果。再看&＃xff08;b&＃xff09;异联想型BM网络&＃xff0c;它的可见节点既是输入节点又是输出节点。当我们输入测试数据时&＃xff0c;从一部分可见节点输入&＃xff0c;从另一部分可见节点输出结果。

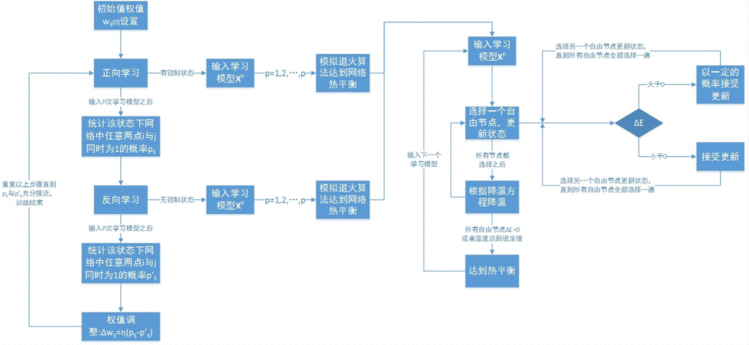
玻尔兹曼机的训练

正向学习阶段&＃xff1a;
　　➢ 自联想型BM网络&＃xff1a;向网络输入信号&＃xff0c;钳制输入输出节点&＃xff0c;让隐节点自由活动
　　➢ 异联想型BM网络&＃xff1a;向网络输入信号&＃xff0c;钳制输入输出节点&＃xff0c;让隐节点自由活动
反向学习阶段&＃xff1a;
　　➢ 自联想型BM网络&＃xff1a;向网络输入信号&＃xff0c;让输入输出节点和隐节点都自由活动
　　➢ 异联想型BM网络&＃xff1a;向网络输入信号&＃xff0c;钳制输入节点&＃xff0c;让输出节点和隐节点自由活动

 

Boltzmann Machine