深度学习-tensorflow学习笔记(1)-MNIST手写字体识别预备知识
在tf第一个例子的时候需要很多预备知识。
-
tf基本知识
-
香农熵
-
交叉熵代价函数cross-entropy
-
卷积神经网络
-
softmax
这里用到的tf基本知识
- tf.tensor-张量,其实就是矩阵。官方说法是原料
- tf.Varible-变量,用来记录数据,参数。其实也是个矩阵。不过要初始化后才有具体的值
- tf.Session()-会话,就是个模型,我们可以在里面添加数据流动方向,运算节点
香农熵
香农熵是计算信息复杂度的公式。
公式如下
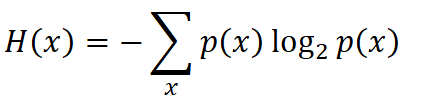
要理解这个公式不难。举例是最好的方法。首先是硬币,正面概率1/2反面1/2
那么H(x)=-(1/2log(1/2)+1/2log(1/2))=1
假如有在某种情况下有4种可能就是
H(x)=-(1/4log(1/4)+1/4log(1/4)+1/4log(1/4)+1/4log(1/4))=2
可以明显看出,问题的分类越多,结果越多,那么复杂度越高。不确定性越高,比如我们在决策树中要做的就是每次都把信息熵最高的选出来然后递归决策
交叉熵代价函数cross-entropy
这是个更优化的损失函数比起常规的cost function.
机器学习中第一个遇见的是sigmod函数,这个函数在开始时梯度小,学习速率慢。我们看下图就知道
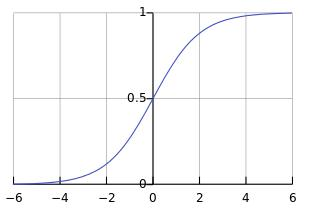
CROSS-ENTROPY解决了初时时学习速率过小的问题
cross-entropy和香农熵的公式有点像,但是千万不要搞混。
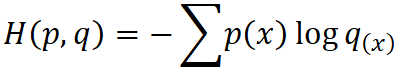
这里的p是样本的真实分布
q是带估计的模型,也就是我们的预测。
同样举例是最好理解公式的方法。
(1)我们假设硬币抛100次正面1/3反面2/3.我们预测是1/2 1/2
然后h(x)=-(1/3*-1+2/3*-1)=1
我们再假设硬币抛100次是正面1/3反2/3 我们预测是正0.001 反0.999
h(x)=-(1/3*负无穷+2/3*0)=正无穷
(2)再假设某种概率都是1/4我们预测也都是1/4
h(x)=-(1/4*-2*4)=2
如果我们预测为1/8 1/4 1/8 1/2
h(x)=-(1/4*-3+1/4*-2+1/4*-3+1/4*-1)=2.25
对比两个例子可以发现,当预测越准时候,交叉熵越小,反之交叉熵越大,(1)中可以看到对于离谱的预测,交叉熵也会变得非常之大
卷积神经网络-以下内容全部来自https://my.oschina.net/u/876354/blog/1620906 一篇超级好的blog
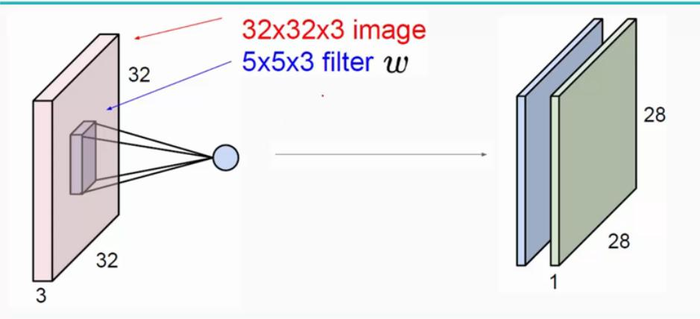
如图卷积层就是图中的filter-它的作用是提取特征值-参考卷积公式
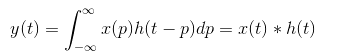 可以知道就是对图像的遍历操作
可以知道就是对图像的遍历操作
这里的卷积层是5*5*3(3是深度这里也就是rgb)所以-一次卷积后得到28*28*3 两次后是24*24*3
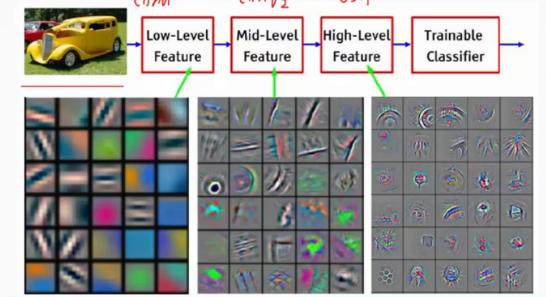
发现一遍超级好文:放下地址
https://my.oschina.net/u/876354/blog/1620906 超级详细的cnn解释
池化层
作用:将图片缩小,减少像素保留特征值,以便后来加快计算。我这里COPY了上面BLOG的部分内容。万一那个BLOG炸了我还有备份
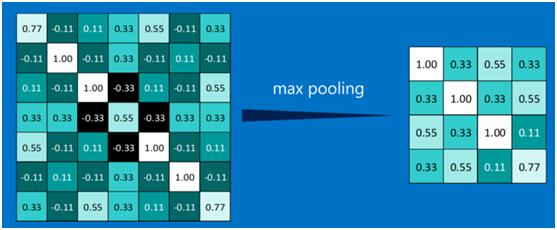
(5)池化(Pooling)
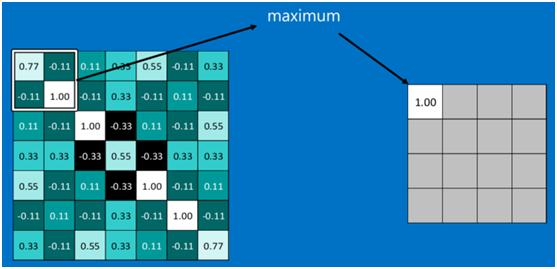
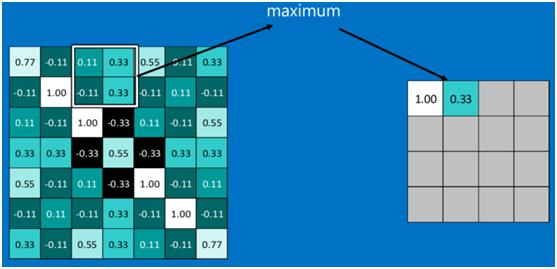
为了有效地减少计算量,CNN使用的另一个有效的工具被称为“池化(Pooling)”。池化就是将输入图像进行缩小,减少像素信息,只保留重要信息。池化的操作也很简单,通常情况下,池化区域是2*2大小,然后按一定规则转换成相应的值,例如取这个池化区域内的最大值(max-pooling)、平均值(mean-pooling)等,以这个值作为结果的像素值。下图显示了左上角2*2池化区域的max-pooling结果,取该区域的最大值max(0.77,-0.11,-0.11,1.00),作为池化后的结果,如下图:

softmax
这是个回归函数,不同于logistic回归解决的二分问题,sotfmax用于多类别问题。
算是激励函数
首先和sigmod一样
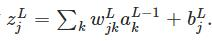
然后
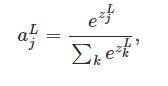
分母是把所有神经元的值加起来
分子是第L层第j个神经元的输出
就是某个神经元输出占所有神经元输出的比值
意义:当它占的比值越大,这个样本的损失越小










 京公网安备 11010802041100号
京公网安备 11010802041100号