作者:520sweet跃_322 | 来源:互联网 | 2023-06-16 09:36
熵(entropy):无损编码事件信息的最小平均编码长度
对每个可能性事件进行编码,计算他们的编码长度,最短的为熵
类似哈夫曼树,编码不能有二义性:
例:四种事件的编码分别为 10、11、 1、110,前两种编码和后两种编码都可组成1110的编码段
| 编码方式 | 猫(50%) | 狗(25%) | 猪(12.5%) | 兔(12.5%) | 编码长度 |
| 方法1 | 10 | 110 | 0 | 111 | 2x50%+3x25%+1x12.5%+3x12.5%=2.25 |
| 方法2 | 0 | 110 | 10 | 111 | 1x50%+3x25%+2x12.5%+2x12.5%=1.875 |
| 方法3 | 0 | 10 | 110 | 111 | 1x50%+2x25%+3x12.5%+3x12.5%=1.75 |
熵的计算公式: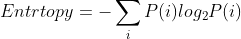
此例的熵为
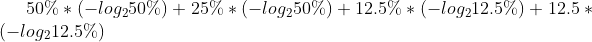
=1.75,与方法3相同
交叉熵
我们用实际的概率分布y和预测的概率分布y_hat进行交叉熵运算
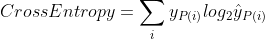
例题:动物数据集中有四种动物,每张照片的label都为one-hot编码
独热编码(one-hot encoding):一个向量,分量和输出类别一样多,类别对应的分量为1其他为0
| 动物 | 猫 | 狗 | 猪 | 兔 |
| label | [1,0,0,0] | [0,1,0,0] | [0,0,1,0] | [0,0,0,1] |
熵: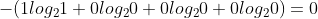
若两不同模型对猫的照片进行预测
| 模型 | 预测 |
| 1 | [0.5,0.2,0.1,0.3] |
| 2 | [0.8,0.1,0.05,0.05] |
模型1的交叉熵: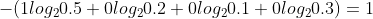
模型2的交叉熵: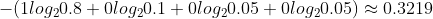
交叉熵越小离熵越近,越准确