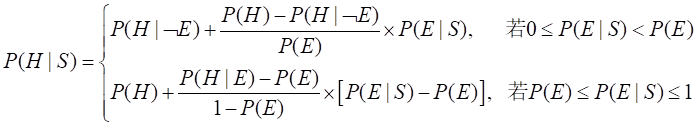目录

 

概述

不确定性推理的含义

基本问题

不确定性推理的类型

可信度推理模型

知识不确定性的表示：

可信度的定义：

可信度的性质

证据不确定性的表示

不确定性的更新

结论不确定性的合成

主观Bayes方法的概率论基础

全概率公式

Bayes公式

推导

知识不确定性的表示

证据不确定性的表示

不确定性的更新

---

概述

不确定性推理的含义

泛指除精确推理以外的其它各种推理问题。包括不完备、不精确知识的推理，模糊知识的推理，非单调性推理等。

采用不确定性推理因：

    所需知识不完备、不精确

    所需知识描述模糊

    多种原因导致同一结论

解题方案不唯一

基本问题

不确定性的表示：

(1) 知识的不确定性的表示

    含义：知识的确定性程度，或动态强度

    表示：用概率，在[0,1]区间取值，越接近于0越假，越接近于1越真

          用可信度，在[-1,1]区间取值，大于0接近于真，小于0接近于假

          用隶属度，在[0,1]区间取值，越接近于0隶属度越低，反之越高

(2) 证据不确定性的表示

    证据的类型：按组织：基本证据，组合证据

                按来源：初始证据，中间结论

    表示方法：概率，可信度，隶属度等

    基本证据：常与知识表示方法一致，如概率，可信度，隶属度等

    组合证据：组合方式：析取的关系，合取的关系。

              计算方法：基于基本证据，最大最小方法，概率方法，有界方法 等。

不确定性的匹配：

含义

    不确定的前提条件与不确定的事实匹配

问题

    前提是不确定的，事实也是不确定的

方法

    设计一个计算相似程度的算法，给出相似的限度

标志

相似度落在规定限度内为匹配，否则为不匹配

不确定性的更新，不确定性结论的合成:

4. 不确定性的更新

    主要问题

    ① 如何用证据的不确定性去更新结论的不确定性

    ② 如何在推理中把初始证据的不确定性传递给最终结论

    解决方法

    对①，不同推理方法的解决方法不同

    对②，不同推理方法的解决方法基本相同，即把当前结论及其不确定性作为新的结论放入综合数据库，依次传递，直到得出最终结论

5. 不确定性结论的合成

    含义：多个不同知识推出同一结论，且不确定性程度不同

方法：视不同推理方法而定

不确定性推理的类型

 

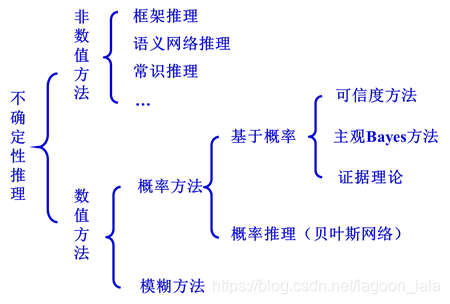
可信度推理模型

知识不确定性的表示：

表示形式：

    在C-F模型中，知识是用产生式规则表示的，其一般形式为：

            IF   E   THEN   H  (CF(H, E))　

其中，E是知识的前提条件；H是知识的结论；CF(H, E)是知识的可信度。

    说明：

     ①  E可以是单一条件，也可以是复合条件。

     ②  H可以是单一结论，也可以是多个结论

     ③  CF是知识的静态强度，CF(H, E)的取值为[-1, 1]，表示当E为真时，证据对H的支持程度，其值越大，支持程度越大。

     例子：

           IF   发烧    AND  流鼻涕   THEN   感冒   (0.8)

表示当某人确实有“发烧”及“流鼻涕”症状时，则有80%的把握是患了感冒。

可信度的定义：

在CF模型中，把CF(H, E)定义为

           CF(H, E)=MB(H, E)-MD(H, E)

式中MB称为信任增长度，MB(H, E)的定义为

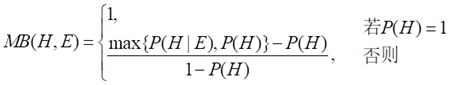
MD称为不信任增长度，MD(H, E)的定义为

    MB和MD的关系

    当MB(H, E)>0时，有P(H|E)>P(H)，即E的出现增加了H的概率

    当MD(H, E)>0时，有P(H|E)

    根据前面对CF(H, E)可信度 、MB(H, E)信任增长度、MD(H, E)不信增长度的定义，可得到CF(H, E)的计算公式：

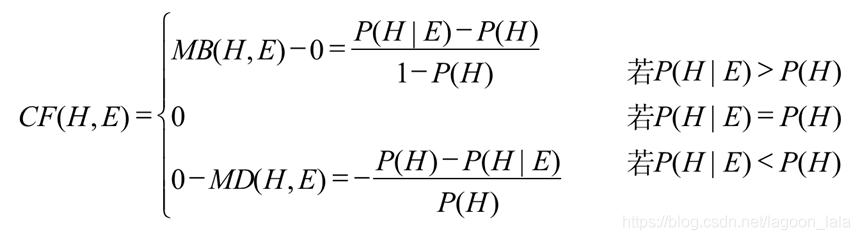
分别解释CF(H,E)>0，CF(H,E)=0，CF(H,E)<0

可信度的性质

    (1)  互斥性

　对同一证据，它不可能既增加对H的信任程度，又同时增加对H的不信任程度，这说明MB与MD是互斥的。即：

         当MB(H, E)>0时，MD(H, E)=0

         当MD(H, E)>0时，MB(H, E)=0

(2) 值域

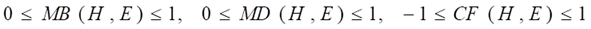
    (3) 典型值

 当CF(H,E)=1时，有P(H/E)=1，它说明由于E所对应证据的出现使H为真。此时，MB(H, E)=1，MD(H, E)=0。

    当CF(H,E)= -1时，有P(H/E)=0，说明由于E所对应证据的出现使H为假。此时，MB(H, E)=0，MD(H,E)=1。

    当CF(H,E)= 0时，有MB(H, E)=0、MD(H, E)=0。E所对应证据的出现不证实、不否认H；

4.

        (1)对H的信任增长度等于对非H的不信任增长度

        (2)对H的可信度与非H的可信度之和等于0

        (3)可信度不是概率，不满足

              P(H)+P(﹁H)=1 和 0≤P(H),P(﹁H)≤ 1

 

 (5)对同一前提E，若支持若干个不同的结论Hi(i=1,2,…,n)，则

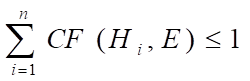
因此，如果发现专家给出的知识有如下情况

        CF(H1, E)=0.7,  CF(H2, E)=0.4

则因0.7+0.4=1.1>1为非法，应进行调整或规范化。

证据不确定性的表示

基本证据

　表示方法，用可信度，其取值范围也为[-1,1]。例如，CF(E) ，其含义：

    CF(E)= 1，证据E肯定它为真

    CF(E)= 0，对证据E一无所知

    0

否定证据

          CF(¬E)= - CF(E)

组合证据

    合取：E=E1 AND E2 AND … En时，若已知CF(E1)，CF(E2)，…，则

           CF(E)=min{CF(E1), CF(E2), … ,CF(En)}

    析取：E=E1 OR  E2  OR … En时，若已知CF(E1)，CF(E2)，…，则

          CF(E)=max{CF(E1), CF(E2), … ,CF(En)}

不确定性的更新

    CF模型中的不确定性推理实际上是从不确定的初始证据出发，不断运用相关的不确性知识，逐步推出最终结论和该结论可信度的过程。而每一次运用不确定性知识，都需要由证据的不确定性和知识的不确定性去计算结论的不确定性。

    不确定性的更新公式

           CF(H)=CF(H, E)×max{0, CF(E)}

    若CF(E)<0，则

           CF(H)=0

即该模型没考虑E为假对H的影响。（只考虑为真条件的影响）

    若CF(E)=1，则

           CF(H)=CF(H,E)

即规则强度CF(H,E)实际上是在E为真时，H的可信度

结论不确定性的合成

    当有多条知识支持同一个结论，且这些知识的前提相互独立，结论的可信度又不相同时，可利用不确定性的合成算法求出结论的综合可信度。

    设有知识：IF  E1   THEN   H  (CF(H, E1))

　　　　　    IF  E2   THEN   H  (CF(H, E2))

则结论H 的综合可信度可分以下两步计算：

    (1) 分别对每条知识求出其CF(H)。即

         CF1(H)=CF(H, E1) ×max{0, CF(E1)}

         CF2(H)=CF(H, E2) ×max{0, CF(E2)}

(2) 用如下公式求E1与E2对H的综合可信度

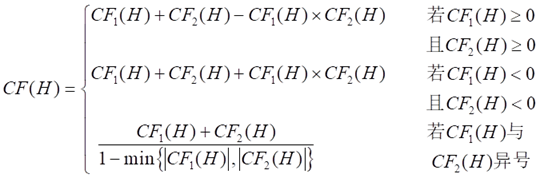
例题P20

主观Bayes方法的概率论基础

全概率公式

定理3.1 设事件A1,A2,…,An满足：

    (1)任意两个事件都互不相容，即当i≠j时，有Ai∩Aj=Φ  (i=1,2,…,n；j=1,2,…,n)；

    (2) P(Ai)>0 (i=1, 2, … ,n);

    (3) D=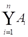

则对任何事件B由下式成立：

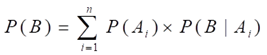
   该公式称为全概率公式，它提供了一种计算P(B)的方法。

Bayes公式

https://blog.csdn.net/jiangjiang_jian/article/details/81346797

　 定理3.2 设事件A1,A2,…,An满足定理3.1规定的条件，则对任何事件B有下式成立：

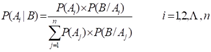
该定理称为Bayes定理，上式称为Bayes公式。

    其中，P(Ai)是事件Ai的先验概率，P(B|Ai)是在事件Ai发生条件下事件B的条件概率；P(Ai|B)是在事件B发生条件下事件Ai的条件概率。

    如果把全概率公式代入Bayes公式，则有：

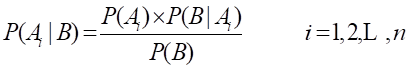
即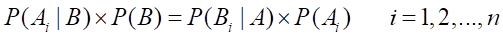

这是Bayes公式的另一种形式。

    Bayes定理给处了用逆概率P(B|Ai)求原概率P(Ai|B)的方法。

贝叶斯公式

在贝叶斯写这篇文章之前，人们已经能够计算“正向概率”，如“假设袋子里面有 N 个白球，M 个黑球，你伸手进去摸一把，摸出黑球的概率是多大”。而一个自然而然的问题是反过来：“如果我们事先并不知道袋子里面黑白球的比例，而是闭着眼睛摸出一个（或好几个）球，观察这些取出来的球的颜色之后，那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。这个问题，就是所谓的逆向概率问题。

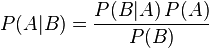
P(A)是 A 的先验概率，之所以称为“先验”是因为它不考虑任何 B 方面的因素

P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。

P(B|A)是已知 A 发生后 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。

P(B)是 B 的先验概率，也作标淮化常量（normalizing constant）。

贝叶斯定理可表述为：

后验概率 = (相似度 * 先验概率)/标淮化常量

也就是说，后验概率与先验概率和相似度的乘积成正比。

另外，比例P(B|A)/P(B)也有时被称作标淮相似度（standardised likelihood），Bayes定理可表述为：

后验概率 = 标淮相似度 * 先验概率

联合概率表示两个事件共同发生（数学概念上的交集）的概率。A 与 B 的联合概率表示为。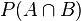

推导

我们可以从条件概率的定义推导出贝叶斯定理。

根据条件概率的定义，在事件 B 发生的条件下事件 A 发生的概率为：

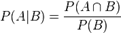
同样地，在事件 A 发生的条件下事件 B 发生的概率为：

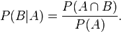
结合这两个方程式，我们可以得到：

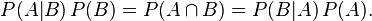
这个引理有时称作概率乘法规则。上式两边同除以 P(A)，若P(A)是非零的，我们可以得到贝叶斯定理:

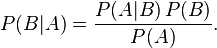
根据新情况更新先验概率-修正概率

知识不确定性的表示

表示形式：在主观Bayes方法中，知识是用产生式表示的，其形式为：

           IF  E  THEN  (LS, LN)   H

其中，(LS, LN)用来表示该知识的知识强度，LS(充分性度量)和LN(必要性度量)的表示形式分别为：

LS充分性：结论成立/不成立时 条件为真概率

LN必要性：结论成立/不成立时 条件为假概率

根据贝叶斯：

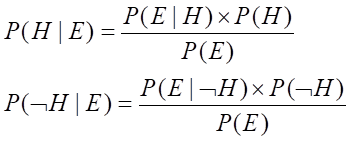
两式相除得（几率函数）：

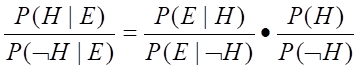
为讨论方便，下面引入几率函数

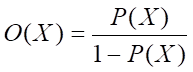
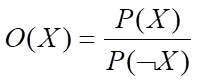
可见，X的几率等于X出现的概率与X不出现的概率之比，P(X)与O(X)的变化一致，且有：

           P(X)=0  时有  O(X)=0

           P(X)=1  时有  O(X)=+∞

即把取值为[0,1]的P(X)放大为取值为[0,+∞]的O(X)

以上两式联立

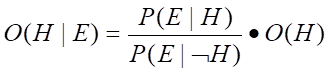
再把LS代入此式，可得：

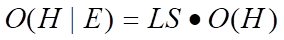
同理可得到关于LN的公式：

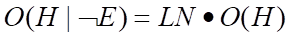
以上两式就是修改的Bayes公式

LS的性质：

    当LS>1时，O(H|E)>O(H)，说明E支持H，LS越大，E对H的支持越充分。当LS→∝时，O(H|E)→∝，即P(H/E)→1，表示由于E的存在将导致H为真。

    当LS=1时，O(H|E)=O(H)，说明E对H没有影响。

　当LS<1时，O(H|E)

　当LS=0时，O(H|E)=0，说明E的存在使H为假。

LN的性质：

　当LN>1时，O(H|﹁E)>O(H)，说明﹁E支持H，即由于E的不出现，增大了H为真的概率。并且，LN得越大，﹁E对H为真的支持就越强。当LN→∝时，O(H|﹁E)→∝，即P(H|﹁E)→1，表示由于﹁E的存在将导致H为真。

    当LN=1时，O(H|﹁E)=O(H)，说明﹁E对H没有影响。

    当LN<1时，O(H|﹁E)

    当LN=0时，O(H|﹁E)=0，说明﹁E的存在（即E不存在）将导致H为假。

 

LS与LN的关系

　由于E和﹁E不会同时支持或同时排斥H，因此只有下述三种情况存在：

    ① LS>1且LN<1                       

    ② LS<1且LN>1                　     

    ③ LS=LN=1

证据不确定性的表示

基本证据的表示：

   在主观Bayes方法中，基本证据E的不精确性是用其概率或几率来表示的。

概率与几率之间的关系为：

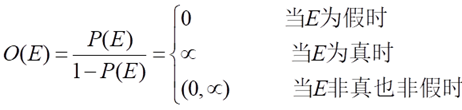
以概率情况为例，对初始证据E，用户可以根据当前观察S将其先验概率P(E)更改为后验概率P(E|S)，即相当于给出证据E的动态强度。

组合证据不确定性的计算：

   证据的基本组合方式只有合取和析取两种。（合取min，析取max）

　当组合证据是多个单一证据的合取时，例

          E=E1  AND   E2  AND  …  AND  En

　如果已知在当前观察S下，每个单一证据Ei有概率P(E1|S), P(E2|S), … ,P(En|S)，则

　　    P(E|S)=min{ P(E1|S), P(E2|S), … ,P(En|S)}

　当组合证据是多个单一证据的析取时，例

             E=E1  OR   E2  OR  …  OR  En

    如果已知在当前观察S下，每个单一证据Ei有概率P(E1|S), P(E2|S), … ,P(En|S)，则

　　P(E|S)=max{ P(E1|S), P(E2|S), … ,P(En|S)}

不确定性的更新

根据E的概率P(E)及LS和LN的值，把H的先验概率P(H)或先验几率O(H)更新为后验概率或后验几率。

    分以下3种情况讨论：

    1. 证据肯定为真

    2. 证据肯定为假

3. 证据既非为真有非为假

证据肯定为真时

　当证据E肯定为真时，P(E)=P(E|S)=1。将H的先验几率更新为后验几率的公式：

          O(H|E)=LS×O(H)

　把H的先验概率P(H)更新为后验概率P(H|E)的公式

 

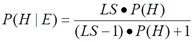
证据既非真假：需要使用杜达等人给出的公式：

P(H|S)=P(H|E)×P(E|S)+P(H|﹁E)×P(﹁E|S)                              (3.7)

 

 

    下面分四种情况讨论：

    (1)P(E|S)=1

    当P(E|S)=1时，P(﹁E|S)=0。

这实际是证据肯定存在的情况

    (2)P(E|S)=0

    当P(E|S)=0时，P(﹁E|S)=1。

    (3)P(E|S)=P(E)

    当P(E|S)=P(E)时，表示E与S无关。由(3.7)式和全概率公式可得

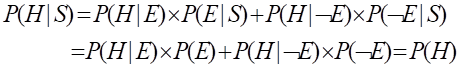
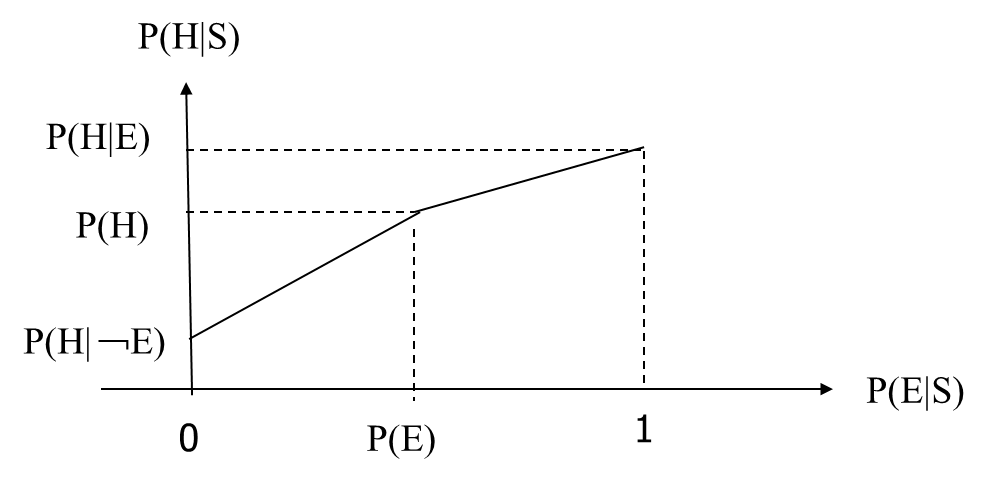
    (4) P(E/S)为其它值

上面已经得到了P(E|S)的3个特殊值：0，P(E),1；它们分别对应的3个值为P(H|﹁E),P(H),P(H|E)。由此构造的分段线性插值函数为：