R正态性检验实例

数据：price.csv文件（一列价格差值的数据，包含标题）

问题描述：

• 利用price.csv数据绘制数据直方图，并添加概率密度曲线(density)和估计概率密度曲线(dnorm) 。


• 绘制出qqplot及其拟合线。


• 用Shapiro和Kolmogorov-Smirnov检验判断该数据是否符合正态分布。

代码实现：

data = read.csv("price.csv", header = T)
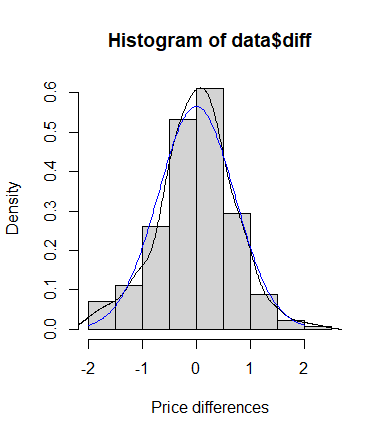
hist(data$diff, freq = F, xlab = 'Price differences', ylab = 'Density') #绘制直方图
lines(density(data$diff), col = 'black') #添加概率密度曲线
x = seq(-2, 2, len = 252)
lines(x, dnorm(x, mean(data$diff), sd(data$diff)), col= 'blue') #添加估计概率密度曲线
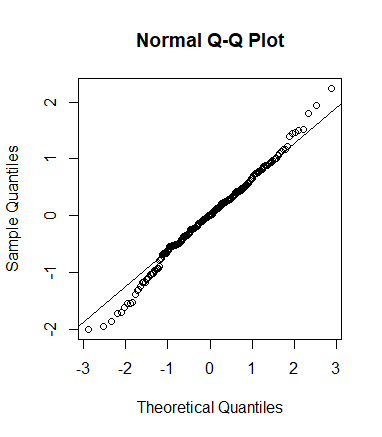
qqnorm(data$diff) #绘制qqplot
qqline(data$diff) #绘制拟合线
shapiro.test(data$diff)
ks.test(data$diff, 'pnorm', mean = mean(data$diff), sd = sd(data$diff))

结果展示：

> shapiro.test(data$diff)
Shapiro-Wilk normality test
data: data$diff
W = 0.99146, p-value = 0.1503
> ks.test(data$diff, 'pnorm', mean = mean(data$diff), sd = sd(data$diff))
One-sample Kolmogorov-Smirnov test
data: data$diff
D = 0.052668, p-value = 0.4867
alternative hypothesis: two-sided

　　两种检验均表明该数据服从正态分布。