算法原理

K最近邻(KNN，k-NearestNeighbor)分类算法是数据挖掘分类技术中最简单的方法之一。

给定测试样本，基于某种距离度量找出训练集中与其最靠近的K个训练样本，然后基于这 K个"邻居"的信息来进行预测。

KNN 算法的核心思想是如果一个样本在特征空间中的 K 个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。

具体步骤

给定训练样本集\(\begin{gather*}S=\{t_1,t_2,t_3...t_s\}\end{gather*}\)和一组类属性\(\begin{gather*}C=\{c_1,c_2,c_3...c_m\}(m\leq s)\end{gather*}\) ，对样本进行分类，KNN 算法的基本步骤为：

（1）先求出 t 与 S 中所有训练样本\(\begin{gather*}t_i(1\leq i \leq s)\end{gather*}\)的距离\(\begin{gather*}dist_{ed}(t,t_i)\end{gather*}\) ，并对所有求出的\(\begin{gather*}dist_{ed}(t,t_i)\end{gather*}\)值递增排序；

（2）选取与待测样本距离最小的 K 个样本，组成集合 N；

（3）统计 N 中 K 个样本所属类别现的频率；

（4）频率最高的类别作为待测样本的类别。

举例说明

如果没看懂上面在说什么，没关系，举个例子这样能更好的理解一下，这里采用的是欧氏距离

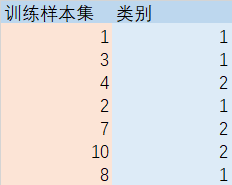
假设 测试集有2和11，其中K=4；对测试集分别计算其与训练集的欧氏距离，得到如下结果

对测试集与训练集的距离进行排序，选取距离最小的前四（k=4）个

在测试集2，距离最小的四个（k=4）训练集数据中，属于类别1的有3个，属于类别2的有1个，所以测试集2的类别为1

在测试集11，距离最小的四个（k=4）训练集数据中，属于类别1的有1个，属于类别2的有3个，所以测试集11的类别为2

相信通过这个例子，大家能够很好的理解KNN算法的具体步骤了。

好了，话不多说，下面还是上代码。

KNN算法代码