作者:nuabolalalala4_135 | 来源:互联网 | 2023-09-07 19:13
转自:https://blog.csdn.net/u012501459/article/details/12945149#creation
相关主题:OpenGL变换,OpenGL投影矩阵,四元数
下载:matrix.zip, matrix_rowmajor.zip
- 概述
- 构造&初始化
- 存取操作
- 矩阵算法
- 变换函数
- 例子:模型视图矩阵
- 例子:投影矩阵
概述
OpenGL为渲染管线准备了4种不同类型的矩阵(GL_MODELVIEW,GL_PROJECTION, GL_TEXTURE and GL_COLOR)并且为这些矩阵提供了变换的操作:glLoadIdentity(),glTranslatef(),glRotatef(),glScalef(),glMultMatrixf(),glFrustum()和glOrtho().
这些内置的矩阵和操作对于开发简单的OpenGL应用程序非常有用并且非常有利于理解矩阵变换。但是当你的应用程序变的复杂的时候,最好是自己为所有需要移动的对象实现你自己的矩阵和操作。除此之外,你也不可以在可编程的管线(GLSL),像OpenGL v3.0+, OpenGL ES v2.0+ 和 WebGL v1.0+中使用这些内置的矩阵和操作。你必须实现你自己的矩阵并且将矩阵中的数据传递到着色器中。
这篇文章提供了一种使用C++编写的独立,通用的的4*4矩阵类Matrix4,并且描述了如果将这个类集成到OpenGL应用程序中。这个类只依赖于定义在Vectors.h中的Vector3和Vector4。这些向量类也包含在 matrix.zip中。
构造&初始化
Matrix4类包含一个16个浮点型元素的数组来存储4*4的矩阵,它有3个构造函数来实例化这个Matrix4类的对象。
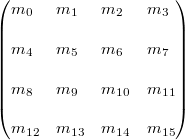
以行为主的Matrix4
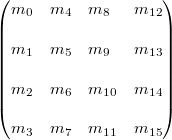
OpenGL中使用的以列为主的矩阵
注意这个Matrix4类使用以行为主的标记次序而不是像OpenGL那样使用以列为主的标记次序。然儿,以行为主的次序和以列为主的次序只是两种不同的将多维数组中的数据存储的一维数组中的方式,这对矩阵的算法和矩阵的操作结果是没有影响的。
缺省的构造函数(没有参数)将会创建一个单位矩阵。其他两个构造函数接受16个参数或者包含16个参数的数组。你也可以使用复制构造或赋值操作符(=)来初始化一个Matrix4类的实例。
顺便说一下,复制构造和赋值操作符(=)会由C++编译器自动生成。
下面是一个使用不同方式构造Matrix4对象的例子。首先,需要在使用Matrix4类的文件中包含Matrices.h头文件。
-
#include "Matrices.h" // 为 Matrix2, Matrix3, Matrix4准备的
-
...
-
-
// 使用缺省的构造函数构造一个单位矩阵
-
Matrix4 m1;
-
-
// 使用16个元素构造一个矩阵
-
Matrix4 m2(1, 1, 1, 1, // 第一行
-
1, 1, 1, 1, // 第二行
-
1, 1, 1, 1, // 第三行
-
1, 1, 1, 1); // 第四行
-
-
// 使用一个数组够造一个矩阵
-
float a[16] = {2,2,2,2, 2,2,2,2, 2,2,2,2, 2,2,2,2};
-
Matrix4 m3(a);
-
-
//使用复制构造和赋值操作符构造一个矩阵
-
Matrix4 m4(m3);
-
Matrix4 m5 = m3;
Matrix4存取操作(Setters/Getters)
Setters
Matrix4类提供set()函数来设置所有的16个元素。
-
Matrix4 m1;
-
-
// 使用16个元素来设置矩阵
-
m1.set(1,1,1,1, 1,1,1,1, 1,1,1,1, 1,1,1,1);
-
-
// 使用数组来设置矩阵
-
float a1[] = {2,2,2,2, 2,2,2,2, 2,2,2,2, 2,2,2,2};
-
m1.set(a1);
你也可以使用setRow()和setColumn()函数一次来设置一行或一列的值,setRow()和setColumn()函数的第一个参数是一个基于0的索引,第二个参数是指向数组的指针。
-
Matrix4 m2;
-
float a2[4] = {2,2,2,2};
-
-
// 使用索引和数组设置一行的值
-
m2.setRow(0, a2); // 1st row
-
-
// 使用索引和数组设置一列的值
-
m2.setColumn(2, a2); // 3rd column
单位矩阵
Matrix4类有一个特殊的setter,identify()函数用来生成一个单位矩阵
-
// 设置一个单位矩阵
-
Matrix4 m3;
-
m3.identity();
Getters
Matrix4::get()方法返回一个指向拥有16个元素的数组。getTranspose()返回转置后的矩阵元素。它专门用来将矩阵中的数据传递到OpenGL中,更多详细的细节参考例子。
-
// 得到矩阵中的元素并赋值个一个数组
-
Matrix4 m4;
-
const float* a = m4.get();
-
-
//将矩阵传递给OpenGL
-
glLoadMatrixf(m4.getTranspose());
访问单个元素
矩阵中的单个元素可以通过[]操作符来访问:
-
Matrix4 m5;
-
float f = m5[0]; // 得到第一个元素
-
-
m5[1] = 2.0f; // 设置第二个元素
打印Matrix4
Matrix4也提供了一个便利的打印输出函数std::cout<<来方便调试&#xff1a;
-
Matrix4 m6;
-
std::cout <
矩阵算法
Matrix4类提供了两个矩阵之间的基本算法。
加法和减法
你可以将两个矩阵相加和相减
-
Matrix4 m1, m2, m3;
-
-
//相加
-
m3 &#61; m1 &#43; m2;
-
m3 &#43;&#61; m1; //等价于: m3 &#61; m3 &#43; m1
-
-
// subtract
-
m3 &#61; m1 - m2;
-
m3 -&#61; m1; // 等价于: m3 &#61; m3 - m1
乘法
你可以将两个矩阵相乘&#xff0c;也有与3维和4维向量相乘以便使用矩阵将向量进行变换。注意矩阵相乘不满足交换律。
-
Matrix4 m1, m2, m3;
-
-
// 矩阵相乘
-
m3 &#61; m1 * m2;
-
m3 *&#61; m1; // 等价于: m3 &#61; m3 * m1
-
-
// 缩放操作
-
m3 &#61; 2 * m1; // 将所有元素缩放
-
-
// 与向量相乘
-
Vector3 v1, v2;
-
v2 &#61; m1 * v1;
-
v2 &#61; v1 * m1; // 前乘
比较
Matrix4类提供了比较操作符来比较两个矩阵中的所有元素&#xff1a;
-
Matrix4 m1, m2;
-
-
//精确比较
-
if(m1 &#61;&#61; m2)
-
std::cout <<"equal" <
-
if(m1 !&#61; m2)
-
std::cout <<"not equal" <
Matrix4变换函数
OpenGL有几个变换函数&#xff1a;glTranslatef(),glRotatef()和glScalef()。Matrix4也提供了几个相同的函数来进行矩阵变换&#xff1a;translate(),rotate()andscale()。除此之外&#xff0c;Matrix4还提供了invert()函数计算矩阵的转置矩阵。
Matrix4::translate(x,y,z)
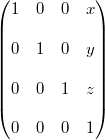
平移矩阵
translate()函数产生经过(x,y,z)变换后的矩阵。首先&#xff0c;它创建一个变换矩阵MT&#xff0c;然后乘以当前矩阵来产生最终的矩阵&#xff1a;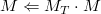
注意这个函数等价于OpenGL中的glTranslatef()&#xff0c;但是OpenGL使用后乘而不是前乘&#xff1a;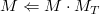 &#xff0c;如果你执行多个变换&#xff0c;结果将会不一样因为矩阵相乘不满足交换律。
&#xff0c;如果你执行多个变换&#xff0c;结果将会不一样因为矩阵相乘不满足交换律。
-
// M1 &#61; Mt * M1
-
Matrix4 m1;
-
m1.translate(1, 2, 3); // 移动到(x, y, z)
Matrix4::rotate(angle,x,y,z)
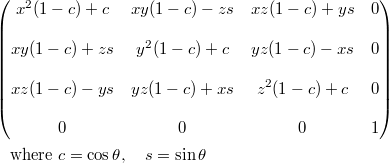
旋转矩阵
rotate()可以被用来通过指定一个轴&#xff08;x&#xff0c;y&#xff0c;z&#xff09;和绕轴旋转的角度来旋转三维模型。这个函数生成一个旋转矩阵MR&#xff0c;然后乘以当前矩阵生成一个最终经过旋转变换后的矩阵&#xff1a;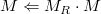
它等价于glRotatef(),但是OpenGL使用后乘操作来生成最终的变换后的矩阵&#xff1a;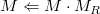
rotate()可以用来绕任意的轴旋转。Matrix4类提供了额外的3个函数绕指定轴旋转rotateX(),rotateY(),rotateZ()。
-
// M1 &#61; Mr * M1
-
Matrix4 m1;
-
m1.rotate(45, 1,0,0); // 绕X轴旋转45度
-
m1.rotateX(45); // 和rotate(45, 1,0,0)一样
Matrix4::scale(x,y,z)

缩放矩阵
scale()在每一个轴上产生一个不均等的缩放效果的矩阵&#xff1a;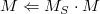 。
。
注意&#xff1a;OpenGL中glScalef()执行后乘操作&#xff1a;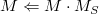 。
。
Matrix4类也提供了均等的缩放函数。
-
// M1 &#61; Ms * M1
-
Matrix4 m1;
-
m1.scale(1,2,3); // 非均等的缩放
-
m1.scale(4); // 均等的缩放&#xff0c;在所有轴上是一样的
Matrix::invert()
invert()函数计算当前矩阵的反转矩阵&#xff0c;这个反转矩阵主要用来将法向量从物体坐标系变换到人眼坐标系中。法向量和顶点的变换不一样。法向量变换是使用GL_MODELVIEW的反转乘以法向量&#xff1a;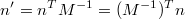 详细的细节参考这儿。
详细的细节参考这儿。
如果矩阵只是欧式变换&#xff08;旋转和平移&#xff09;&#xff0c;或者放射变换&#xff08;旋转&#xff0c;平移&#xff0c;缩放&#xff0c;裁剪&#xff09;&#xff0c;反转矩阵的计算会很简单。Matrix4::invert()将会为你决定何时的反转方式&#xff0c;但是如果你明确地调用了一个反转函数:invertEuclidean(),invertAffine(),invertProjective()o或invertGeneral()。请阅读 Matrices.cpp中的详细细节。
-
Matrix4 m1;
-
m1.invert(); // 反转矩阵
例子&#xff1a;模型视图矩阵
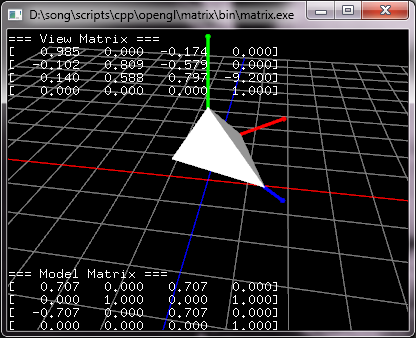
下载源文件和二进制文件&#xff1a;matrix.zip
这个例子显示了怎么将Matrix4类集成到OpenGL程序中。GL_MODELVIEW联合和视图矩阵和模型矩阵&#xff0c;但是我们将它们分开并传递两个矩阵给OpenGL的模型视图矩阵。
-
Matrix4 matModel, matView, matModelView;
-
glMatrixMode(GL_MODELVIEW);
-
...
-
-
// 视图变换
-
matView.identity(); // 变换次序:
-
matView.rotate(-camAngleY, 0,1,0); // 1: 绕Y轴旋转
-
matView.rotate(-camAngleX, 1,0,0); // 2: 绕X轴旋转
-
matView.translate(0, 0, -camDist); // 3: 沿Z轴平移
-
-
//模型变换
-
// 沿Y轴旋转45度&#xff0c;然后向上平移两个单位
-
matModel.identity();
-
matModel.rotate(45, 0,1,0); // 第一个变换
-
matModel.translate(0, 2, 0); // 第二次变换
-
-
//构造模型视图矩阵: Mmv &#61; Mv * Mm
-
matModelView &#61; matView * matModel;
-
-
// 将模型视图矩阵传递给OpenGL
-
// 注意&#xff1a;需要将矩阵转置
-
glLoadMatrixf(matModelView.getTranspose());
-
-
// 绘制
-
...
等价的OpenGL实现如下&#xff1a;
-
//注意&#xff1a;变换的次序是相反的
-
//因为OpenGL使用的是后乘
-
glMatrixMode(GL_MODELVIEW);
-
glLoadIdentity();
-
-
// 视图变换
-
glTranslatef(0, 0, -camDist); // 3: 沿Z轴平移
-
glRotatef(-camAngleX, 1,0,0); // 2: 绕X轴旋转
-
glRotatef(-camAngleY, 0,1,0); // 1: 绕Y轴旋转
-
-
// 模型变换
-
// 先绕Y轴旋转45度再向上平移2个单位
-
glTranslatef(0, 2, 0); // 2&#xff1a;平移
-
glRotatef(45, 0,1,0); // 1&#xff1a; 旋转
-
-
// 绘制
-
...
模型视图矩阵的反转用来将法向量从物体坐标系变换到人眼坐标系中。在可编程的渲染管线中&#xff0c;你需要将它传递给GLSL着色器。
-
//为法向量构造矩阵: (M^-1)^T
-
Matrix4 matNormal &#61; matModelView; // 得到模型视图矩阵
-
matNormal.invert(); // 得到反转矩阵
-
matNormal.transpose(); // 将矩阵转置
例子&#xff1a;投影矩阵
这个例子显示了如何创建投影矩阵&#xff0c;等价于glFrustum()和glOrtho()。更多细节查看source codes。
-
// 设置投影矩阵并将其传递给OpenGL
-
Matrix4 matProject &#61; setFrustum(-1, 1, -1, 1, 1, 100);
-
-
glMatrixMode(GL_PROJECTION);
-
glLoadMatrixf(matProject.getTranspose());
-
...
-
-
///
-
// glFrustum()
-
///
-
Matrix4 setFrustum(float l, float r, float b, float t, float n, float f)
-
{
-
Matrix4 mat;
-
mat[0] &#61; 2 * n / (r - l);
-
mat[2] &#61; (r &#43; l) / (r - l);
-
mat[5] &#61; 2 * n / (t - b);
-
mat[6] &#61; (t &#43; b) / (t - b);
-
mat[10] &#61; -(f &#43; n) / (f - n);
-
mat[11] &#61; -(2 * f * n) / (f - n);
-
mat[14] &#61; -1;
-
mat[15] &#61; 0;
-
return mat;
-
}
-
-
///
-
// gluPerspective()
-
///
-
Matrix4 setFrustum(float fovY, float aspect, float front, float back)
-
{
-
float tangent &#61; tanf(fovY/2 * DEG2RAD); // 视角一半的切
-
float height &#61; front * tangent; // 近平面高度的一半
-
float width &#61; height * aspect; // 近平面宽度的一半
-
-
// 参数: left, right, bottom, top, near, far
-
return setFrustum(-width, width, -height, height, front, back);
-
}
-
-
///
-
// glOrtho()
-
///
-
Matrix4 setOrthoFrustum(float l, float r, float b, float t, float n, float f)
-
{
-
Matrix4 mat;
-
mat[0] &#61; 2 / (r - l);
-
mat[3] &#61; -(r &#43; l) / (r - l);
-
mat[5] &#61; 2 / (t - b);
-
mat[7] &#61; -(t &#43; b) / (t - b);
-
mat[10] &#61; -2 / (f - n);
-
mat[11] &#61; -(f &#43; n) / (f - n);
-
return mat;
-
}
-