NavicatforMariaDB15：可视化数据洞察与智能图表功能详解

Navicat 15 具备多项改进和新功能，能满足你对数据库开发的需求。过百种增强的功能和耳目一新的界面，让你以崭新的方式创建、管理和维护数据库。（安装教程，请查看图片水印链接!）

智能图表

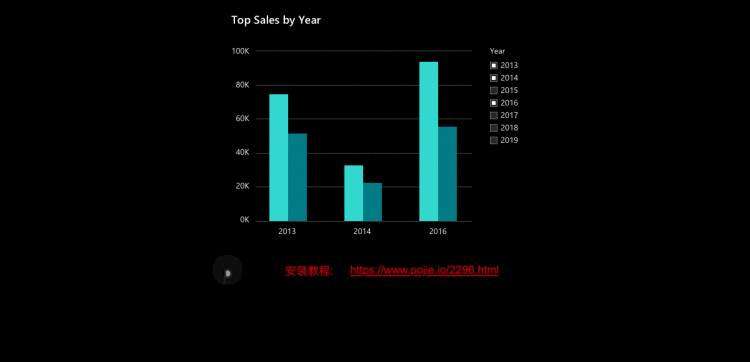
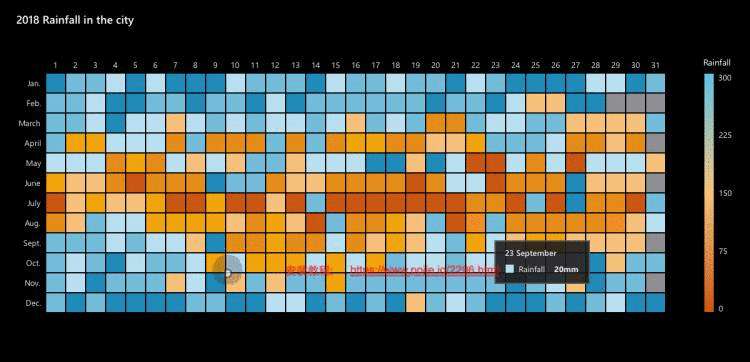
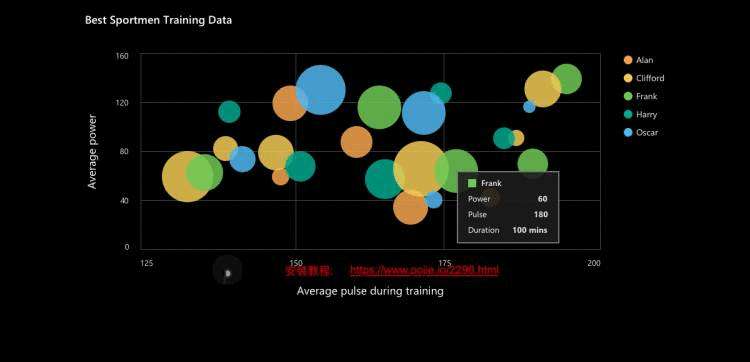
智能图表助你更好地了解自己的数据。我们新的数据可视化工具使你可以将数据转换为有效的图像，以标识趋势、模式和离群值。简化数据分析并将你的工作区共享给同事，以更好地支持你的业务决策和策略。

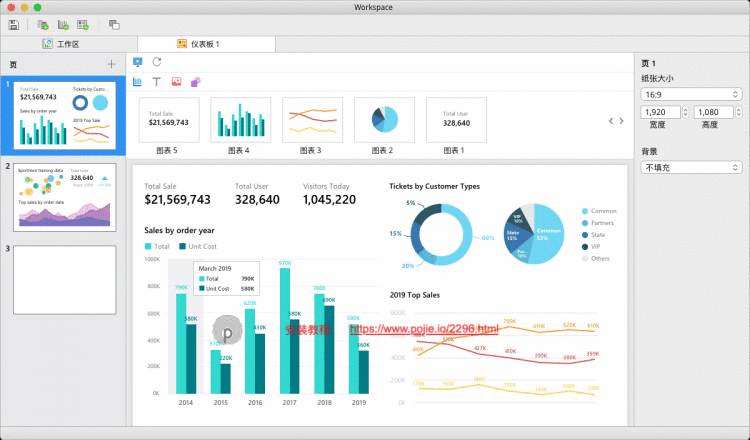
创建图表的简单步骤

在 Navicat 15 中，创建有意义的图表并不是困难复杂的事。只需 3 个简单的步骤就能创建一个易于阅读的图表。

步骤 1：指定图表使用的数据源。

步骤 2：构建图表。

步骤 3：在仪表板中显示图表。

高阶的图表

Navicat 15 支持 20 种图表类型。选择一个最合适的类型，以确保你的数据能清晰准确地呈现。