MPC控制算法代码matlab实现，matlabfunc实现，自编写matlabfunction实现MPC算法

MPC工具箱提供的MPC模块不能实现权重参数的实时修改&＃xff0c;有必要自己编写一个实现模型预测控制算法的matlab function。

• 主义事项

求解QP问题的时候使用哪一个函数更好&＃xff1f;&＃xff1f;&＃xff1f;&＃xff1f;

mpcqpsolver   (To be removed) Solve a quadratic programming problem using the KWIK algorithm

quadprog

mpcInteriorPointSolver

以下物理量必须设置相同&＃xff0c;不然容易报错或求解不出理论控制量&＃xff1a;

1. matlab func模块的调用频率

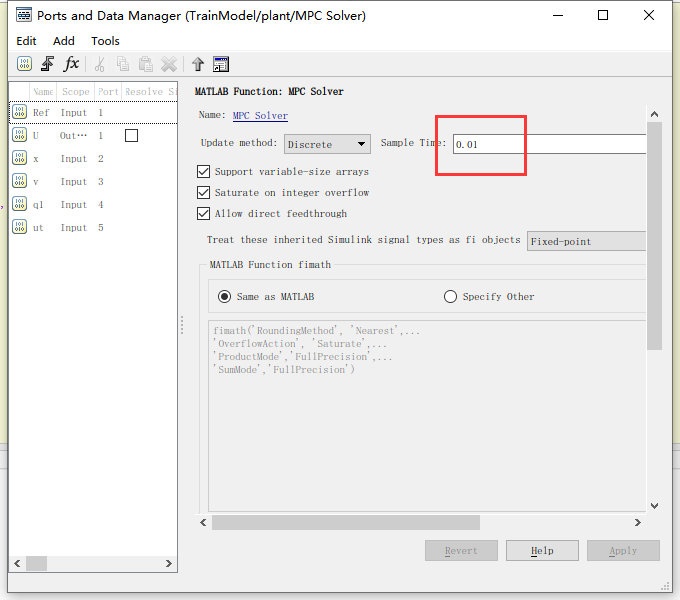
2. MPC算法的采样频率。

3. 被控对象的状态空间方程的离散化频率。

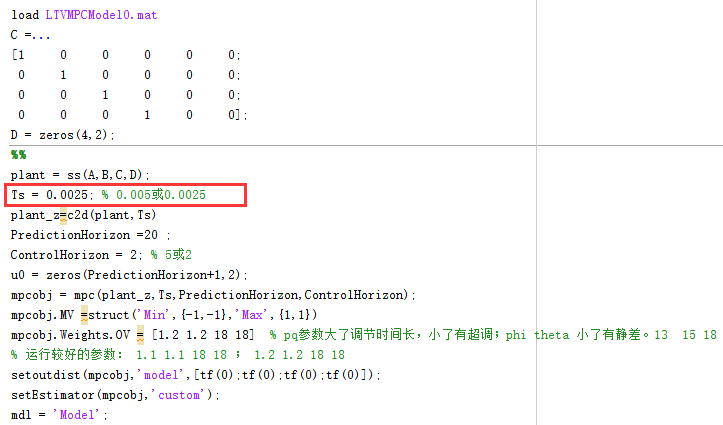
以一个双积分系统为例子&＃xff0c;MPC的实现代码如下

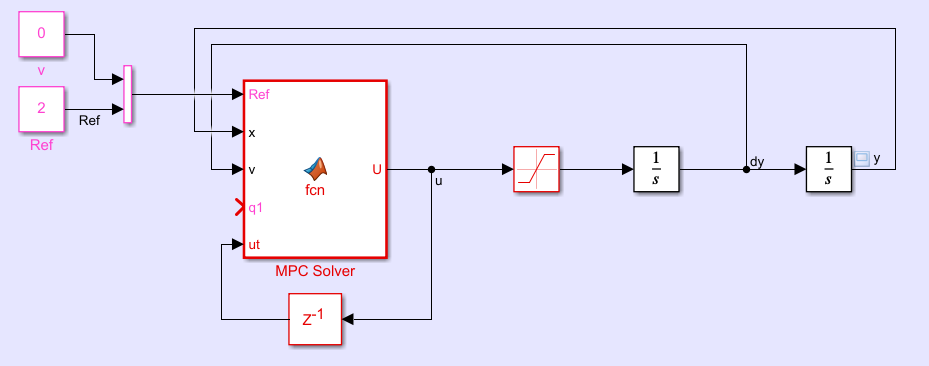
function U &＃61; fcn(Ref,x,v,q1,ut)
% clear
% s&＃61;tf(&＃39;s&＃39;)
% G&＃61;1/s^2
% G&＃61;ss(G)
% A&＃61;G.A
% B&＃61;G.B
% C&＃61;eye(2)
% D&＃61;zeros(2,1)
% sys&＃61;ss(A,B,C,D)
% plant&＃61;c2d(sys,0.01)
coder.extrinsic(&＃39;quadprog&＃39;);
U &＃61; 0;
deltaU &＃61;0;Ak &＃61; ...[1 0;0.01 1];Bk &＃61; ...
[0.01;
5e-05];Ck&＃61;eye(2);
Dk&＃61;zeros(2,1);dk&＃61;zeros(6,1);
ek&＃61;zeros(4,1);
% 权重矩阵
Q&＃61;diag([1.5&＃43;q1,100]); % 1.52 100 2.8
R&＃61;diag([0]);
S&＃61;diag([0]);
pho&＃61;0.05;
e&＃61;0.1;Ts&＃61;0.01;xk&＃61;[v;x;ut];
yref&＃61;Ref;% 维数说明
m&＃61;1; % 控制
n&＃61;2; % 状态变量
n0&＃61;m&＃43;n; % 新的状态维度
Hc&＃61;2;
Hp&＃61;10;
p&＃61;size(Ck,1) ; %输出量维数
% 已知量
u_1 &＃61; ut;
U_1&＃61;kron(ones(Hc,1),u_1);
% syms deltau deltau1 deltau2 deltau3 deltau4
% deltaU&＃61;[deltau;deltau1;deltau2;deltau3;deltau4]
% U&＃61;M*deltaU&＃43;U_1%% 令 x&＃61;[x(k);u(k-1)] 控制量变为 delta u 则新系统的状态空间为
Ak&＃61;[ Ak,Bk;zeros(m,n),eye(m) ];
Bk&＃61;[Bk;eye(m)];
Ck&＃61;[Ck,Dk];
Dk&＃61;Dk;
dk&＃61;[dk;zeros(m,1)];
ek&＃61;ek;
%% 预测输出矩阵 k&＃43;1 ... K&＃43;Hp 共Hp个
% 控制输出矩阵 k...K&＃43;Hc-1 共Hc个% compute PSIk
[m1,n1]&＃61;size(Ck*Ak);
PSIk&＃61;zeros(m1*Hp , n1);
for i&＃61;1:HpPSIk( (i-1)*m1&＃43;1 :(i-1)*m1&＃43;m1 , 1:n1)&＃61;Ck*Ak^i;
end
% compute THETAk
[m2,n2]&＃61;size(Ck*Bk);
THETAk&＃61;zeros(m2*Hp , n2*Hc);
for i&＃61;1:Hpfor j&＃61;1:Hcif i>&＃61;jTHETAk( (i-1)*m2&＃43;1:(i-1)*m2&＃43;m2, (j-1)*n2&＃43;1:(j-1)*n2&＃43;n2 ) &＃61; Ck*Ak^(i-j)*Bk;elseif j-i&＃61;&＃61;1THETAk( (i-1)*m2&＃43;1:(i-1)*m2&＃43;m2, (j-1)*n2&＃43;1:(j-1)*n2&＃43;n2)&＃61;Dk;elseTHETAk( (i-1)*m2&＃43;1:(i-1)*m2&＃43;m2, (j-1)*n2&＃43;1:(j-1)*n2&＃43;n2)&＃61;zeros(m2,n2);endend
end
% compute TAUk
[m3,n3]&＃61;size(Ck);
TAUk&＃61;zeros(m3*Hp , n3*Hp);
for i&＃61;1:Hpfor j&＃61;1:Hpif i>&＃61;jTAUk( (i-1)*m3&＃43;1:(i-1)*m3&＃43;m3, (j-1)*n3&＃43;1:(j-1)*n3&＃43;n3 ) &＃61; Ck*Ak^(i-j);elseTAUk( (i-1)*m3&＃43;1:(i-1)*m3&＃43;m3, (j-1)*n3&＃43;1:(j-1)*n3&＃43;n3)&＃61;zeros(m3,n3);endend
end
% compute PHIk
PHIk&＃61;zeros(n0*Hp,1);
% compute LAMBDA
LAMBDAk&＃61;zeros(p*Hp,1); %% 线性时变时候不为0&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;% compute Qe
[m4,n4]&＃61;size(Q);
Qe&＃61;zeros(m4*Hp,n4*Hp);
for i&＃61;1:Hpfor j&＃61;1:Hpif i&＃61;&＃61;jQe( (i-1)*m4&＃43;1:(i-1)*m4&＃43;m4, (j-1)*n4&＃43;1:(j-1)*n4&＃43;n4 ) &＃61; Q;elseQe( (i-1)*m4&＃43;1:(i-1)*m4&＃43;m4, (j-1)*n4&＃43;1:(j-1)*n4&＃43;n4 )&＃61;zeros(m4,n4);endend
end
% compute Re
[m5,n5]&＃61;size(R);
Re&＃61;zeros(m5*Hc,n5*Hc);
for i&＃61;1:Hcfor j&＃61;1:Hcif i&＃61;&＃61;jRe( (i-1)*m5&＃43;1:(i-1)*m5&＃43;m5, (j-1)*n5&＃43;1:(j-1)*n5&＃43;n5 ) &＃61; R;elseRe( (i-1)*m5&＃43;1:(i-1)*m5&＃43;m5, (j-1)*n5&＃43;1:(j-1)*n5&＃43;n5 )&＃61;zeros(m5,n5);endend
end
% compute Se
[m6,n6]&＃61;size(S);
Se&＃61;zeros(m6*Hc,n6*Hc);
for i&＃61;1:Hcfor j&＃61;1:Hcif i&＃61;&＃61;jSe( (i-1)*m6&＃43;1:(i-1)*m6&＃43;m6, (j-1)*n6&＃43;1:(j-1)*n6&＃43;n6 ) &＃61; S;elseSe( (i-1)*m6&＃43;1:(i-1)*m6&＃43;m6, (j-1)*n6&＃43;1:(j-1)*n6&＃43;n6 )&＃61;zeros(m6,n6);endend
endK&＃61;tril(ones(Hc));
Im&＃61;eye(m,m);
M&＃61;kron(K,Im);[m7,n7]&＃61;size(yref);
Yrefk&＃61;zeros(m7*Hp,1);
for i&＃61;1:HpYrefk( (i-1)*m7&＃43;1:(i-1)*m7&＃43;m7 , 1)&＃61;yref;
end
epsilon&＃61;PSIk*xk&＃43;TAUk*PHIk&＃43;LAMBDAk-Yrefk;
%% 最终变量 Hk Gk Pk
Hk&＃61;...[ 2*(THETAk&＃39;*Qe*THETAk&＃43;Re&＃43;M&＃39;*Se*M) , zeros(m*Hc,1) ;zeros(1,m*Hc) , pho ];Gk&＃61;...[ 2*epsilon&＃39;*Qe*THETAk&＃43;2*U_1&＃39;*Se*M , 0 ];Pk&＃61;...[ epsilon&＃39;*Qe*epsilon &＃43; U_1&＃39;*Se*U_1 &＃43; pho*e^2 ];%% QP问题
H&＃61;Hk;
c&＃61;Gk&＃39;;
A&＃61;[];
b&＃61;[];
Aeq&＃61;[];
beq&＃61;[];
Minv&＃61;M^-1;
VLB&＃61;[Minv*(-ones(m*Hc,1)-U_1);-1];
VUB&＃61;[Minv*(ones(m*Hc,1)-U_1);1];
[x,z,fla,out]&＃61;quadprog(H,c,A,b,Aeq,beq,VLB,VUB);
deltaU &＃61; x(1);U &＃61; ut(1)&＃43;deltaU ;

MPC算法的参考文献为&＃xff1a;

基于模型预测控制的无人驾驶车辆轨迹跟踪控制算法研究_孙银健

&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;

声明&＃xff1a;若果您觉得您被侵犯了权利&＃xff0c;请联系本博客作者&＃xff0c;同样的&＃xff0c;若引用了本文也请注明出处。

&＃xff01;&＃xff01;&＃xff01;&＃xff01;&＃xff01;

需要源代码、slx文件或技术支持的童鞋请联系我。