岭回归及其应用

岭回归基本原理

岭回归是一种用于处理多重共线性问题的回归方法。其基本思想是在普通最小二乘法的基础上，加入一个L2正则项，以减少模型的复杂度和过拟合风险。岭回归的代价函数形式如下：

其中，第一个部分是残差平方和，第二个部分是L2正则项，λ是正则化参数。通过调整λ的值，可以在模型的偏差和方差之间找到一个平衡点。

选择合适的λ值是岭回归的关键。通常，可以通过交叉验证等方法来确定最优的λ值。下图展示了不同λ值对模型参数的影响：

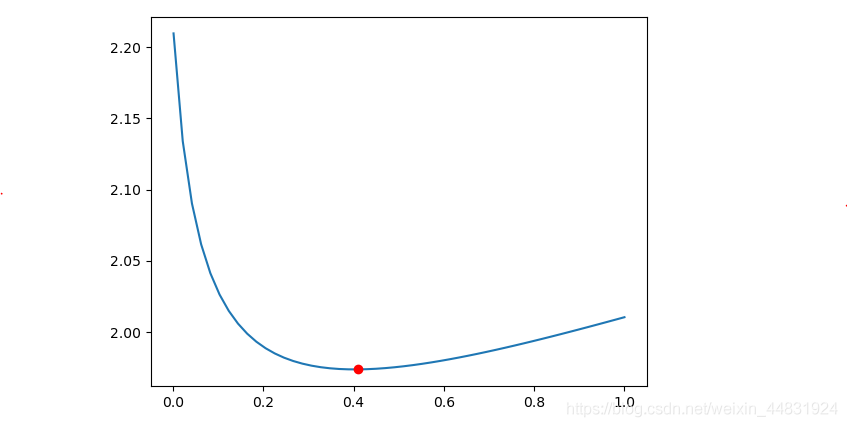
从图中可以看出，随着λ值的增加，各参数的值逐渐趋于稳定。因此，选择合适的λ值可以使模型更加稳定和准确。

sklearn实现岭回归

下面是一个使用Python和sklearn库实现岭回归的例子。我们将使用Longley数据集，该数据集包含了一些宏观经济指标，如GNP平减指数、GNP、失业率等。

import numpy as np
from numpy import genfromtxt
from sklearn import linear_model
import matplotlib.pyplot as plt

# 读入数据
data = genfromtxt(r"longley.csv", delimiter=',')
print(data)

# 切分数据
x_data = data[1:, 2:]
y_data = data[1:, 1]
print(x_data)
print(y_data)

# 生成50个候选的λ值
alphas_to_test = np.linspace(0.001, 1)

# 创建模型
model = linear_model.RidgeCV(alphas=alphas_to_test, store_cv_values=True)
model.fit(x_data, y_data)

# 输出最优的λ值
print(model.alpha_)

# 输出每个λ值对应的loss值
print(model.cv_values_.shape)

# 绘制λ值与loss值的关系图
plt.plot(alphas_to_test, model.cv_values_.mean(axis=0))
plt.plot(model.alpha_, min(model.cv_values_.mean(axis=0)), 'ro')
plt.show()

# 预测
print(model.predict(x_data[2, np.newaxis]))

运行结果如下：

[[ nan nan nan nan nan nan nan nan]
 [ nan 83. 234.289 235.6 159. 107.608 1947. 60.323]
 [ nan 88.5 259.426 232.5 145.6 108.632 1948. 61.122]
 [ nan 88.2 258.054 368.2 161.6 109.773 1949. 60.171]
 [ nan 89.5 284.599 335.1 165. 110.929 1950. 61.187]
 [ nan 96.2 328.975 209.9 309.9 112.075 1951. 63.221]
 [ nan 98.1 346.999 193.2 359.4 113.27 1952. 63.639]
 [ nan 99. 365.385 187. 354.7 115.094 1953. 64.989]
 [ nan 100. 363.112 357.8 335. 116.219 1954. 63.761]
 [ nan 101.2 397.469 290.4 304.8 117.388 1955. 66.019]
 [ nan 104.6 419.18 282.2 285.7 118.734 1956. 67.857]
 [ nan 108.4 442.769 293.6 279.8 120.445 1957. 68.169]
 [ nan 110.8 444.546 468.1 263.7 121.95 1958. 66.513]
 [ nan 112.6 482.704 381.3 255.2 123.366 1959. 68.655]
 [ nan 114.2 502.601 393.1 251.4 125.368 1960. 69.564]
 [ nan 115.7 518.173 480.6 257.2 127.852 1961. 69.331]
 [ nan 116.9 554.894 400.7 282.7 130.081 1962. 70.551]]

[[ 234.289 235.6 159. 107.608 1947. 60.323]
 [ 259.426 232.5 145.6 108.632 1948. 61.122]
 [ 258.054 368.2 161.6 109.773 1949. 60.171]
 [ 284.599 335.1 165. 110.929 1950. 61.187]
 [ 328.975 209.9 309.9 112.075 1951. 63.221]
 [ 346.999 193.2 359.4 113.27 1952. 63.639]
 [ 365.385 187. 354.7 115.094 1953. 64.989]
 [ 363.112 357.8 335. 116.219 1954. 63.761]
 [ 397.469 290.4 304.8 117.388 1955. 66.019]
 [ 419.18 282.2 285.7 118.734 1956. 67.857]
 [ 442.769 293.6 279.8 120.445 1957. 68.169]
 [ 444.546 468.1 263.7 121.95 1958. 66.513]
 [ 482.704 381.3 255.2 123.366 1959. 68.655]
 [ 502.601 393.1 251.4 125.368 1960. 69.564]
 [ 518.173 480.6 257.2 127.852 1961. 69.331]
 [ 554.894 400.7 282.7 130.081 1962. 70.551]]

[ 83. 88.5 88.2 89.5 96.2 98.1 99. 100. 101.2 104.6 108.4 110.8
 112.6 114.2 115.7 116.9]
0.40875510204081633
(16, 50)