
名师支招:考场战术分享

珠海市第一中学数学科组长潘静总结历年数学高考经验,从“考前建议”“考试策略”“考场战术”三个方面,给考生准备了详细的备考攻略与答题技巧。
锦囊1

考前建议→保温、熟悉、适应
①保温——
做适当有代表性的保温习题,特别是重点、典型题型,要保持解题思维的灵活与流畅。
②熟悉——
熟悉数学高频考点中的概念、公式、定理以及典型方法,并清楚其适用范围与使用条件。
③适应——
适应高考数学在下午15:00-17:00的时间段,尽量安排在下午复习数学,保持良好状态。
锦囊2

考试策略→先易后难
数学试卷总分150分,容易题、中档题与难题比例约为3:5:2。先抢会做的题,接着抢有门的题,然后才拼有困难的题,最后再抠不会的题。先抢占有利地势,可以保证在有限的时间内少丢分、多拿分。
①先易——
重点落实占比80%的容易题和中档题的性价比最高。花的时间少,得的分数多,一般花80-90分钟左右就可以得到110-120左右的分数。所以应该做到认真对待,完整规范争取少丢分、不丢分。
②后难——
将难题与新题留到第二阶段来完成才有锦上添花的效果。
基础题答完后,考生达到了热身与兴奋,才是更有效解决难题的最佳时机,才能争取在难题环节拿到分、多拿分。
对于难题,如果不是完全不会做,就要坚持把你会的写出来展示思维过程,甚至跳步到直接做第二问答题、跨步答题,放弃其中难度很大的步骤,能够争取得分机会。
锦囊3

考场战术→仔细审题 掌握时间
①入场——
符合考场要求的考试用品与考试证件应准备齐全,入场前一定要仔细检查一遍。
②开考——
(1)清查试卷完整状况,在答题卡上清晰准确地填好个人信息。
(2)用眼用手不用笔,浏览试卷并粗略分出基础题、难题新题两类,为解题时“先易后难”作准备。
(3)稳定情绪:我易人易,我不大意;我难人难,我不畏难。
③考中——
(1)把会做的题都做对是胜利,把不会做的题抢几分是功劳,收获80%就是成功。
审题:确认条件无漏、路子对了再做下去。
计算:步骤规范一点,错误常常出在“算错了”,计算时草稿也要写好步骤,确认了再往下走。
考察:考虑问题全面一点,提防陷阱,注意疏漏,多从概念、公式、法则、图形中去考察,尤其考察是否有特例,考虑结论是否符合题意,分类要明,讨论要全。
(2)落实考试策略,合理分配时间,保证总分。
试题设置:12道选择题、4道填空题、5道大题和1道二选一题,应该坚持由易到难的做题顺序。
时间分配:选择、填空题(约40分钟);解答题(约80分钟),其中前2道解答题防止犯运算和表述错误,平均用时10分钟左右,选考题是概念和简单运算,要细心又要快,用时10分钟左右,另外3道解答题防止犯审题错误,以及第一问会而不做和耗时过多的错误,平均用时在15分钟左右。
一步到位:要养成一次就做对,一步到位的习惯。不要养成回过头来检查的习惯。高考时设置的最后15分钟哨声,就是提醒部分考生保证把会做的题做好。


解题方法与技巧

供参考
1. 解决绝对值问题(化简、求值、方程、不等式、函数),把含绝对值的问题转化为不含绝对值的问题。具体转化方法有:
(1)分类讨论法:根据绝对值符号中的数或式子的正、零、负分情况去掉绝对值。
(2)零点分段讨论法:适用于含一个字母的多个绝对值的情况。
(3)两边平方法:适用于两边非负的方程或不等式。
(4)几何意义法:适用于有明显几何意义的情况。
2.根据项数选择方法和按照一般步骤是顺利进行因式分解的重要技巧。因式分解的一般步骤是:

3. 利用完全平方公式把一个式子或部分化为完全平方式就是配方法,它是数学中的重要方法和技巧。配方法的主要根据有:
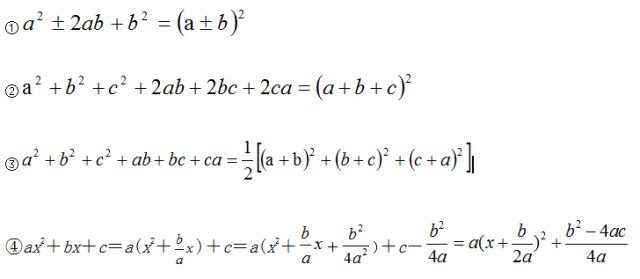
4. 解某些复杂的特型方程要用到:换元法。换元法解方程的一般步骤是:

5. 待定系数法是在已知对象形式的条件下求对象的一种方法。适用于求点的坐标、函数解析式、曲线方程等重要问题的解决。其解题步骤是:
(1)设
(2)列
(3)解
(4)写
6. 复杂代数等式型条件的使用技巧:
左边化零,右边变形
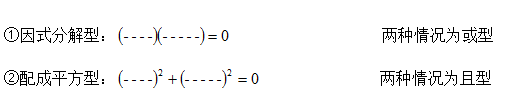
7. 数学中两个最伟大的解题思路:

8. 化简二次根式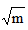 的基本思路是:
的基本思路是:
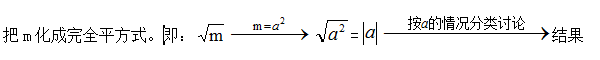
9. 化简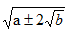 的方法是观察法:
的方法是观察法:
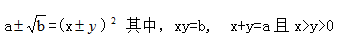
10. 代数式求值的方法有:
(1)直接代入法
(2)化简代入法
(3)适当变形法(和积代入法)
注意:当求值的代数式是字母的“对称式”时,通常可以化为字母“和与积”的形式,从而用“和积代入法”求值。
11. 方程中除过未知数以外,含有的其它字母叫参数,这种方程叫含参方程。解含参方程一般要用“分类讨论法”,其原则是:
(1)按照类型求解
(2)根据需要讨论
(3)分类写出结论
12. 恒相等成立的有用条件:

13. 由一元二次不等式解集为R的有关结论容易得到下列恒不等成立的条件:

14. 图像的平移规律是研究复杂函数的重要方法。平移规律是:

15. 讨论函数性质的重要方法是图像法——看图像、得性质。

16. 函数、方程、不等式间的重要关系: 
17.一元二次不等式的解法:
一元二次不等式可以用因式分解转化为二元一次不等式组去解,但比较复杂;它的简便的实用解法是根据“三个二次”间的关系,利用二次函数的图像去解。具体步骤如下:

18.一元二次方程根的讨论:
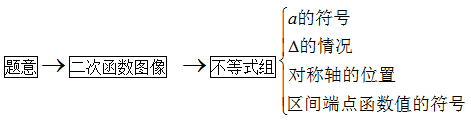
一元二次方程根的符号问题或m型问题可以利用根的判别式和根与系数的关系来解决,但根的一般问题、特别是区间根的问题要根据“三个二次”间的关系,利用二次函数的图像来解决。“图像法”解决一元二次方程根的问题的一般思路是:
19. 基本函数在区间上的值域
我们学过的一次函数、反比例函数、二次函数等有名称的函数是基本函数。基本函数求值域或最值有两种情况:
(1)定义域没有特别限制时---记忆法或结论法;
(2)定义域有特别限制时——图像截断法,一般思路是:
20.最值型应用题的解法
应用题中,涉及“一个变量取什么值时另一个变量取得最大值或最小值”的问题是最值型应用题。解决最值型应用题的基本思路是函数思想法,其解题步骤是:
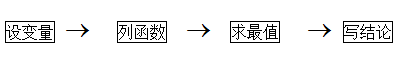
21. 穿线法是解高次不等式和分式不等式的最好方法。其一般思路是:
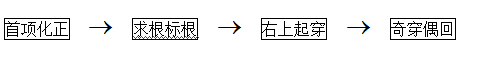 注意:
注意:
(1)高次不等式首先要用移项和因式分解的方法化为“左边乘积、右边是零”的形式。
(2)分式不等式一般不能用两边都乘去分母的方法来解,要通过移项、通分合并、因式分解的方法化为“商零式”,用穿线法解。


常用公式及结论


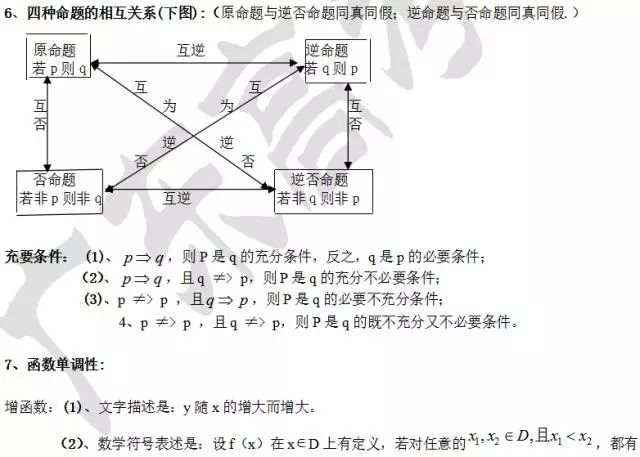

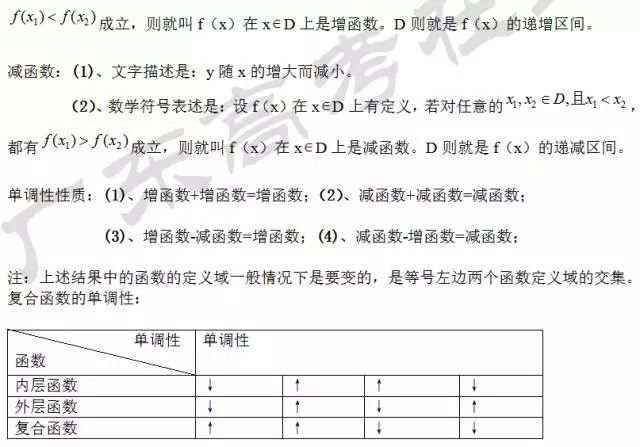
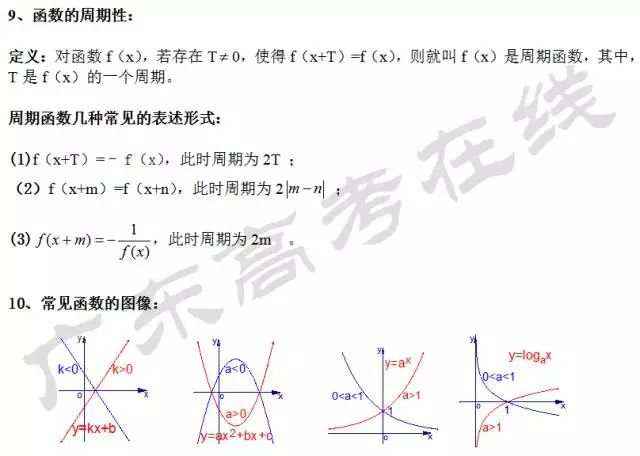











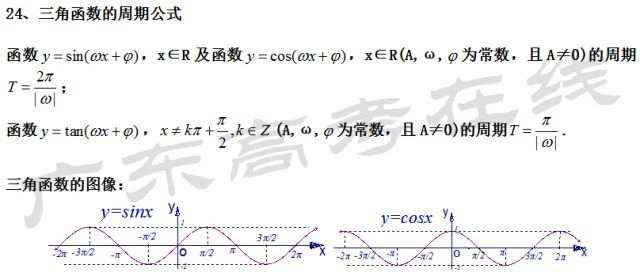
























文末,来个小彩蛋!
在无计可施时,
同学们可参考以下做法↓
(当然,会的同学请自行屏蔽以下内容 )
)


以上内容由广东高考在线综合
广东高考在线小程序:
“我要考大学”
各类招考政策 各校招生章程
全国高校介绍 投档和专业分
知识方法梳理 咨询交流进步
按排位或成绩查往年可填志愿
点击下图马上使用↓↓
点击【在看】,考得好看!
 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有