LeetCode：189.轮转数组（Java）

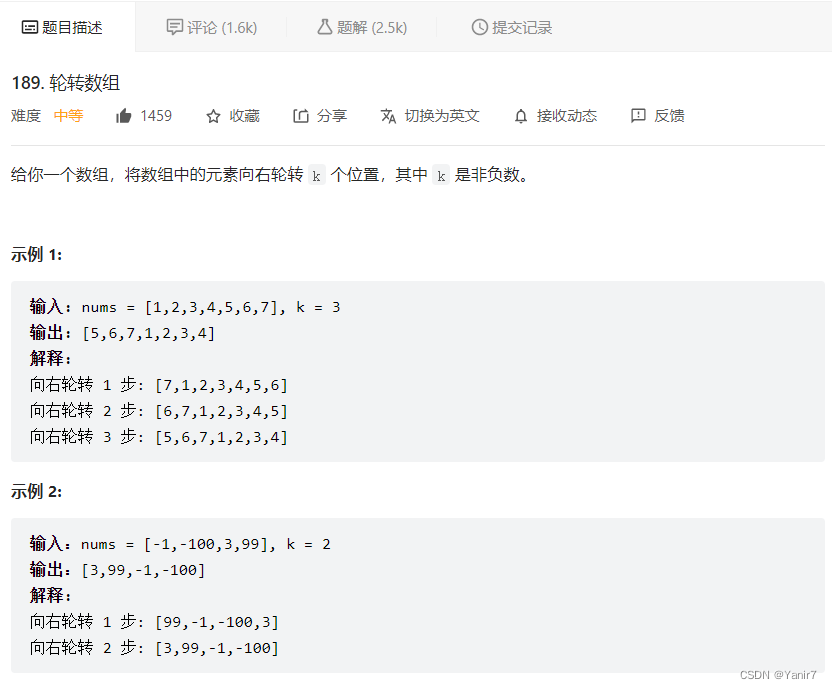
方法1&＃xff1a; 跳序 轮转法——带标记&＃xff0c;时间复杂度和空间复杂度均为O(n)

因为有些特殊情况&＃xff0c;会陷入循环&＃xff0c;比如这个例子&＃xff1a;

我不知道怎么处理这种情况&＃xff0c;所以直接搞个标记数组falgs[]来看看这个位置的数字是否被处理过。方法二来改进这个陷入循环的问题

class Solution {public void rotate(int[] nums, int k) {// 1.跳序 轮转法——带标记&＃xff0c;时间复杂度和空间复杂度均为O(n)int len&＃61;nums.length;int[] flags&＃61;new int[len];Arrays.fill(flags,0);int next;int curr&＃61;0;int tmp&＃61;nums[curr]; //临时保存上一个int tmp1; //临时保存当前的int n&＃61;len;while(n!&＃61;0 && k!&＃61;0){// if(n!&＃61;len && len%k&＃61;&＃61;0 &&n%(len/k)&＃61;&＃61;0){// curr&＃43;&＃43;;// tmp&＃61;nums[curr];// }next&＃61;(curr&＃43;k)%len;while(flags[next]&＃61;&＃61;1){next&＃61;(next&＃43;1)%len;if(flags[next]&＃61;&＃61;1)continue;else {curr&＃61;next;tmp &＃61; nums[curr];next &＃61; (curr &＃43; k) % len;}}tmp1&＃61;nums[next];nums[next]&＃61;tmp;tmp&＃61;tmp1;curr&＃61;next;flags[curr]&＃61;1;n--;}}
}

方法2&＃xff1a;类1-跳序轮转法——不借助flag数组 

这里稍微对pos&＃61;&＃61;i解释一下&＃xff0c;因为pos如果一次陷入循环&＃xff0c;意味着pos会在不同的轮转中循环&＃xff0c;即跳出一个轮回会进入下一个轮换&＃xff0c;在每个轮回中都会陷入循环。pos是从0开始&＃xff0c;那当pos跳转一轮回到起点0以后&＃xff0c;就派i&＃xff08;可以看做pos的初始&＃xff09;对线&＃xff0c;发现跟初始0一样&＃xff0c;就开始对pos&＃43;1处理。

&＃xff08;我们把这样叫一次轮转&＃xff0c;从pos&＃61;0出发&＃xff0c;回到pos&＃61;0&＃xff09;

class Solution {public void rotate(int[] nums, int k) {// 5.类1-跳转轮转法&＃xff1a;他人解法&＃xff0c;不借助flag数组int len &＃61; nums.length,n &＃61; len;int i &＃61; 0,pos &＃61; 0, pre &＃61; nums[pos],temp &＃61; nums[pos];if(k%n &＃61;&＃61; 0) return;while (n-- !&＃61; 0) {pos &＃61; (pos &＃43; k) % len;temp &＃61; nums[pos];nums[pos] &＃61; pre;pre &＃61; temp;if (pos &＃61;&＃61; i) { // 避免陷入循环pos &＃61; &＃43;&＃43;i;pre &＃61; nums[pos];temp &＃61; nums[pos];}}}
}

方法3&＃xff1a;借助另外一个数组保存每次移动的数——以空间换时间

class Solution {public void rotate(int[] nums, int k) {// 双数组&＃xff1a;顺序 轮转法——借助另一个数组。int len&＃61;nums.length;int[] res&＃61;Arrays.copyOf(nums,len);int next;for(int i&＃61;0;i}

方法4&＃xff1a;翻转数组——有点巧妙的

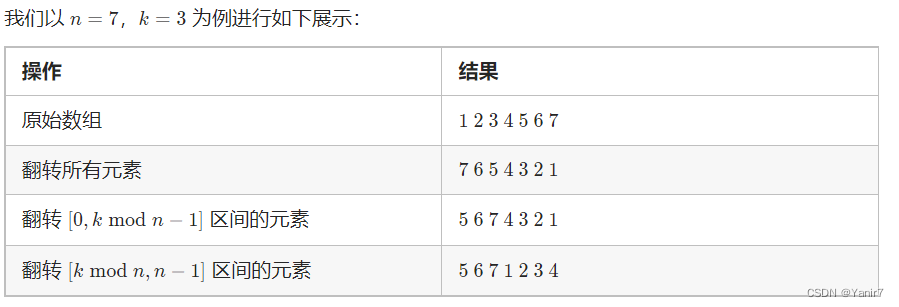
class Solution {public void rotate(int[] nums, int k) { // 4.三次翻转数组&＃xff0c;找出k%n的那个位置点——耗时最少int len&＃61;nums.length;int pos&＃61;k%(len);reverse(nums,0,len);reverse(nums,0,pos);reverse(nums,pos,len);}public void reverse(int[] nums,int start,int end){int tmp;int i&＃61;0;while(i<(end-start)/2){tmp&＃61;nums[end-1-i];nums[end-1-i]&＃61;nums[start&＃43;i];nums[start&＃43;i]&＃61;tmp;i&＃43;&＃43;;}}
}

方法5&＃xff1a;每次向前移动一位&＃xff0c;重复k次&＃xff08;超出时间限制&＃xff09;

class Solution {public void rotate(int[] nums, int k) {// 3.单次轮转k次法O(n*k)——超出时间限制×int len&＃61;nums.length;int tmp;while((k--)!&＃61;0){tmp&＃61;nums[0];for(int i&＃61;1;i}