作者:mobiledu2502858037 | 来源:互联网 | 2023-08-16 07:14
在上一篇博文中,我们一起学习了决策树中的ID3算法,知道了如何选择决策树分裂的属性。但是我们细心一想,在ID3算法中仍然有几方面的不足:
1. 在ID3算法当中,选择分裂的属性的时候,依据是信息增益,其实信息增益用作分裂的依据并不如信息增益率(information gain ratio)。
2. ID3算法不能对连续的数据进行处理,只能将连续的数据离散化处理。
3. ID3算法并没有做剪枝处理,导致决策树可能会过于复杂导致过拟合。
所以在这里,我们提出一种基于ID3算法的优化算法—C4.5算法,为了说清楚这个C4.5,我们还是沿用上一篇博文中的股票数据。
| 今日股票涨跌 | 上证指数 | 涨跌幅 | 明日股票涨跌 |
|---|
| + | 2983 | +1.2 | - |
| - | 2962 | -6.6 | + |
| + | 3008 | +7.0 | - |
| - | 2966 | -3.2 | - |
| + | 3018 | +5.7 | + |
| - | 2995 | -2.2 | + |
| + | 2899 | +1.7 | - |
| - | 3065 | -0.6 | + |
| + | 2888 | +0.2 | - |
| - | 3112 | -9.3 | + |
首先我们来看看信息增益率的公式吧:
Info_Ratio=Info_GainInstrinsicInfoInfo_Ratio=Info_GainInstrinsicInfo
其中Info_Gain就是我们上一篇博文中给出的公式:
Info_Gain=Entropy−∑i∈Ipi⋅EntropyiInfo_Gain=Entropy−∑i∈Ipi⋅Entropyi
在信息增益的公式中,分母InstrinsicInfo表示分裂子节点数据量的信息增益,也就是分裂节点的熵计算公式如下:
InstrinsicInfo=−∑i=1mniN⋅log2(niN)InstrinsicInfo=−∑i=1mniN⋅log2(niN)
在这个公式中ni表示子节点的数据量,N表示父节点的数据量。同理,信息增益率越大,表示分裂的效果越好。为了计算说明,我们就不像上一篇博文那样每一种属性都计算一遍了,我们就拿今日股票涨跌来做例子吧。

在上一篇博文中我计算了信息增益Info_Gain=0.278,接着我们来计算子节点数据量的信息增益InstrinsicInfo:
InstrinsicInfo=−∑i=1mniN⋅log2(niN)=−(12log212)×2=1InstrinsicInfo=−∑i=1mniN⋅log2(niN)=−(12log212)×2=1
所以以今日股票涨跌作为分裂属性的信息增益率 = Info_Gain/InstrinsicInfo=0.278。
讲到这里,有的朋友就会说,如果我用上证指数这种连续型属性作为分类属性,数据应该怎么处理?这里就涉及到了对连续性属性的处理。我们首先对上证指数进行一个从低到高的排序:
| 今日股票涨跌 | 上证指数 | 涨跌幅 | 明日股票涨跌 |
|---|
| + | 2888 | +0.2 | - |
| + | 2899 | +1.7 | - |
| - | 2962 | -6.6 | + |
| - | 2966 | -3.2 | - |
| + | 2983 | +1.2 | - |
| - | 2995 | -2.2 | + |
| + | 3008 | +7.0 | - |
| + | 3018 | +5.7 | + |
| - | 3065 | -0.6 | + |
| - | 3112 | -9.3 | + |
其实在上一篇博文中我以上证指数3000点为界限来作为切割线,也就是在2995和3008之间划分一条切割线来分裂,这种做法其实是不科学的。其实这10组数据就会有9条可能的分割线来为决策树做分裂,我们最科学的方法是计算每一种分裂方法的信息增益率,然后取最大的一条分割线。如图所示:
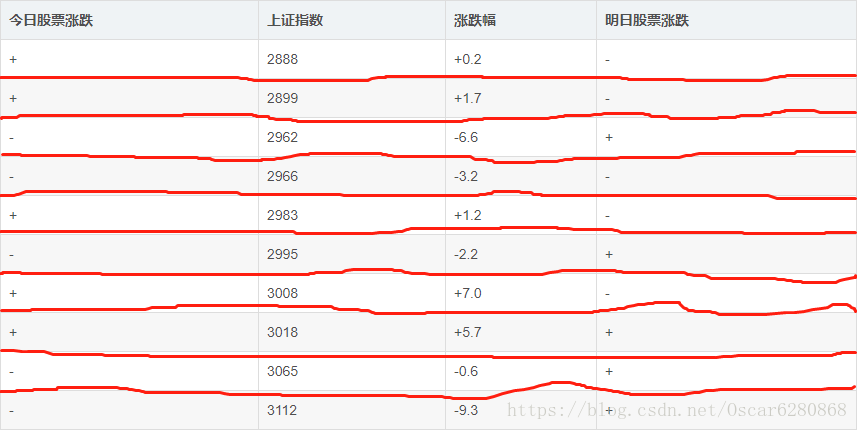
不好意思,画的时候手有点抖,凑合看一下。这样划分的话,其实计算量很大的,我们想个办法来优化一下,如图所示: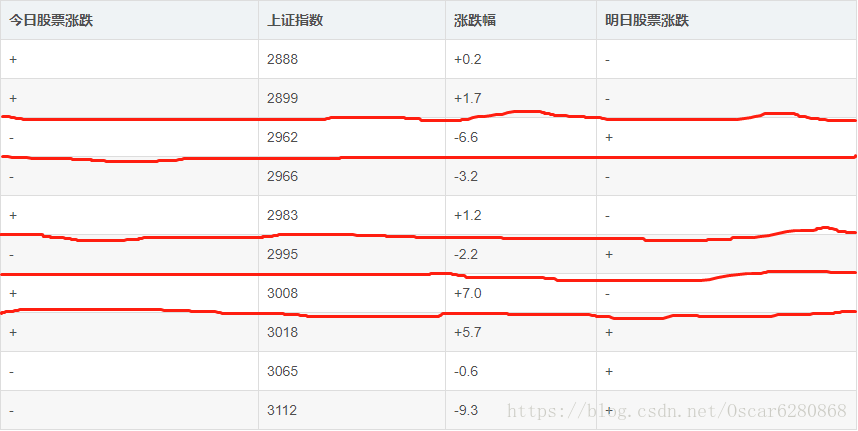
我们来看图中第一行和第二行中明日股票的涨跌都是跌,可以把这看做一类,不必在这两组数据之间做分割,如果强行把这两组在一类的数据分割,那么效果肯定不如把他们归为一类。所以同理,我们可以得到图中的分割线,这样本来有9条分割线降低到了5条,这样可以降低了计算的复杂度。
说完了上面的这些,我们再来说一下剪枝,剪枝其实就是在完全生长的决策树基础上,对分类不理想的子树做修剪,从而降低决策树的复杂度,防止决策树的过拟合,让决策树达到一个理想的状态。决策树的剪枝可以分成两类,一类是先剪枝一类是后剪枝,先剪枝的意思是提前结束决策树的生长,后剪枝的意思是在决策树构造完毕之后再进行剪枝操作。在C4.5算法中采用的是悲观剪枝法(PEP),就是说如果决策树的精度在剪枝之后没有降低的话,那么就进行剪枝操作。这里有朋友就要提出问题了,什么样叫决策树的精度没有降低?我们用数学的角度来看看,这里有判决是否进行剪枝操作的数学公式:
Eleaf⩽Esubtree+S(Esubtree)Eleaf⩽Esubtree+S(Esubtree)
在这个公式中Eleaf表示子节点的误差,Esubtree表示子树的误差。可以把子树的误差精度理解成满足二项分布,所以根据二项分布特性:
Esubtree=∑i=1m(ei+0.5),S(Esubtree)=np(1−p)−−−−−−−−√,p=EsubtreeNEsubtree=∑i=1m(ei+0.5),S(Esubtree)=np(1−p),p=EsubtreeN
其中N是子树的数据量。在上述公式中,0.5表示的是修正因子,因为对父节点的分裂总会得到比父节点分类结果更好的效果,所以子节点的误差会大于父节点的误差,为了让父节点的误差不小于子节点的误差,所以要加上一个修正因子。我们来举一个例子:

我们可以计算得到:
Esubtree=∑i=1m(ei+0.5)=(2+0.5)+(1+0.5)+(1+0.5)=5.5Esubtree=∑i=1m(ei+0.5)=(2+0.5)+(1+0.5)+(1+0.5)=5.5
S(Esubtree)=np(1−p)−−−−−−−−√=5.5(1−5.515)−−−−−−−−−−√=1.866S(Esubtree)=np(1−p)=5.5(1−5.515)=1.866
Eleaf=e+0.5=6+0.5=6.5Eleaf=e+0.5=6+0.5=6.5
所以满足公式:
Eleaf<Esubtree&#43;S(Esubtree)Eleaf
所以对于上述决策树来说&#xff0c;应该进行剪枝操作。这就是我们的C4.5决策树&#xff0c;希望对您有所帮助&#xff0c;本人能力有限&#xff0c;如有纰漏请轻喷&#xff0c;不吝指教。如有转载&#xff0c;请标明出处&#xff0c;谢谢。