机器学习算法（五）——最优化方法：梯度下降

一、什么是梯度下降

梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。

在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。

在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。

1-1、什么是梯度

梯度实际上就是多变量微分的一般化。

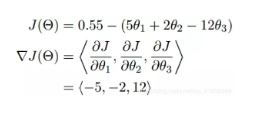
我们可以看到，梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用<>包括起来，说明梯度其实一个向量。

梯度是微积分中一个很重要的概念，之前提到过梯度的意义

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率。

在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向。

这也就说明了为什么我们需要千方百计的求取梯度。

我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的方向一直走，就能走到局部的最低点！

二、理解梯度下降

很多求解最优化问题的方法，大多源自于模拟生活中的某个过程。比如模拟生物繁殖，得到遗传算法。模拟钢铁冶炼的冷却过程，得到退火算法。其实梯度下降算法就是模拟滚动，或者下山，在数学上可以通过函数的导数来达到这个模拟的效果。
梯度下降算法是一种思想，没有严格的定义。

2-1、场景假设

梯度下降就是从群山中山顶找一条最短的路走到山谷最低的地方。

既然是选择一个方向下山，那么这个方向怎么选？每次该怎么走？选方向在算法中是以随机方式给出的，这也是造成有时候走不到真正最低点的原因。如果选定了方向，以后每走一步，都是选择最陡的方向，直到最低点。
总结起来就一句话：随机选择一个方向，然后每次迈步都选择最陡的方向，直到这个方向上能达到的最低点。

梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：

一个人被困在山上，需要从山顶到山谷。
但此时雾很大，看不清下山的路径。他必须利用自己周围的信息去找到下山的路径。
这个时候，他就可以利用梯度下降算法来帮助自己下山。
具体来说就是，以他当前的所处的位置为基准，随机选择一个方向，然后每次迈步都选择最陡的方向。
然后每走一段距离，都反复采用同一个方法：如果发现脚下的路是下坡，就顺着最陡的方向走一步，如果发现脚下的路是上坡，就逆着方向走一步，最后就能成功的抵达山谷。

2-2、数学推导

https://blog.csdn.net/pengchengliu/article/details/80932232

三、实现梯度下降

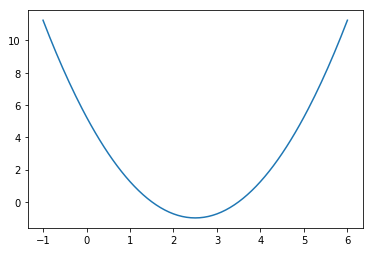
创建损失函数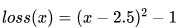，在（-1,6）中构建140个点，并求出对应的损失函数值。

import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative

def lossFunction(x):
	return (x-2.5)**2-1

# 在-1到6的范围内构建140个点
plot_x = np.linspace(-1,6,141)
# plot_y 是对应的损失函数值
plot_y = lossFunction(plot_x)

plt.plot(plot_x,plot_y)
plt.show()

已知梯度下降的本质是多元函数的导数，这里定义一个求导的方法，使用的是scipy库中的derivative方法。

"""
算法：计算损失函数J在当前点的对应导数
输入：当前数据点theta
输出：点在损失函数上的导数
"""
def dLF(theta):
	return derivative(lossFunction, theta, dx=1e-6)

接下来我们就可以进行梯度下降的操作了。首先我们需要定义一个点θ作为初始值，正常应该是随机的点，但是这里先直接定为0。然后需要定义学习率η，也就是每次下降的步长。这样的话，点θ每次沿着梯度的反方向移动η距离，即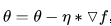，然后循环这一下降过程。

那么还有一个问题：如何结束循环呢？梯度下降的目的是找到一个点，使得损失函数值最小，因为梯度是不断下降的，所以新的点对应的损失函数值在不断减小，但是差值会越来越小，因此我们可以设定一个非常小的数作为阈值，如果说损失函数的差值减小到比阈值还小，我们就认为已经找到了。

theta = 0.0
eta = 0.1
epsilon = 1e-6
while True:
	# 每一轮循环后，要求当前这个点的梯度是多少
	gradient = dLF(theta)
	last_theta = theta
	# 移动点，沿梯度的反方向移动步长eta
	theta = theta - eta * gradient
	# 判断theta是否达到最小值
	# 因为梯度在不断下降，因此新theta的损失函数在不断减小
	# 看差值是否达到了要求
	if(abs(lossFunction(theta) - lossFunction(last_theta)) 		break
print(theta)
print(lossFunction(theta))

"""
输出：
2.498732349398569
-0.9999983930619527
"""

下面可以创建一个用于存放所有点位置的列表，然后将其在图上绘制出来。
为了方便测试，可以将其封装成函数进行调用。

def gradient_descent(initial_theta, eta, epsilon=1e-6):
	theta = initial_theta
	theta_history.append(theta)
	while True:
		# 每一轮循环后，要求当前这个点的梯度是多少
		gradient = dLF(theta)
		last_theta = theta
		# 移动点，沿梯度的反方向移动步长eta
		theta = theta - eta * gradient
		theta_history.append(theta)
		# 判断theta是否达到损失函数最小值的位置
		if(abs(lossFunction(theta) - lossFunction(last_theta)) 			break

def plot_theta_history():
	plt.plot(plot_x,plot_y)
	plt.plot(np.array(theta_history), lossFunction(np.array(theta_history)), color="red", marker="o")
	plt.show()

首先使用学习率η=0.1，进行观察：
eta=0.1
theta_history = []
gradient_descent(0., eta)
plot_theta_history()
print("梯度下降查找次数：",len(theta_history))

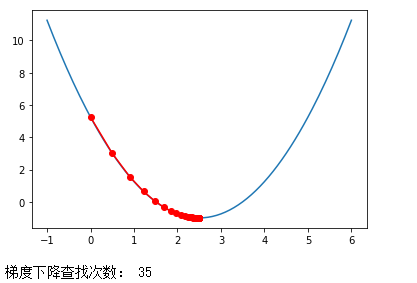
学习率变低了，每一步都很小，因此需要花费更多的步数。

调大学习率η，

eta=0.9
theta_history = []
gradient_descent(0., eta)
plot_theta_history()
print("梯度下降查找次数：",len(theta_history))

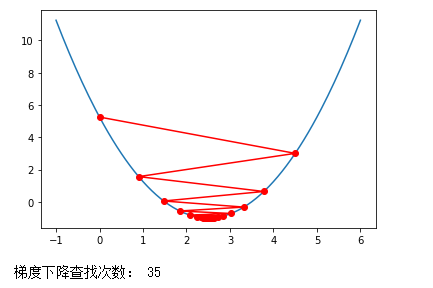
可见在一定范围内将学习率调大，还是会逐渐收敛的。但是我们要注意，如果学习率调的过大， 一步迈到“损失函数值增加”的点上去了，在错误的道路上越走越远，就会导致不收敛，会报OverflowError的异常。

为了避免报错，可以对原代码进行改进：
在计算损失函数值时捕获一场

def lossFunction(x):
	try:
		return (x-2.5)**2-1
	except:
		return float("inf")

设定条件，结束死循环

def gradient_descent(initial_theta, eta, n_iters, epsilon=1e-6):
	theta = initial_theta
	theta_history.append(theta)
	i_iters = 0
	while i_iters 		gradient = dLF(theta)
		last_theta = theta
		theta = theta - eta * gradient
		theta_history.append(theta)
		if(abs(lossFunction(theta) - lossFunction(last_theta)) 			break
		i_iters += 1