首先,直接给出AdaBoost算法的核心思想是:在原数据集上经过取样,来生成不同的弱分类器,最终再把这些弱分类器聚合起来。
关键问题有如下几个:
(1)取样怎样用数学方式表达出来;
(2)每次取样依据什么准则;
(3)最后怎么聚合这些弱分类器。
首先我们看第一个问题,如何表示取样?答案使用原数据集上的加权error。
假设我们对数据集D做的取样如下:
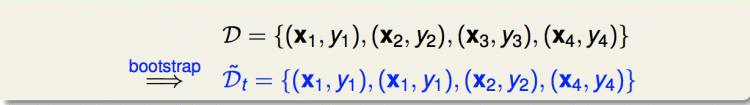
那么我们在新数据集上的01error可以等效为在原数据集上的加权error:

即我们取样相当于确定一组权重μ,对这个加权的error作最小化就能得到一个弱分类器g。
特别的,对于svm和逻辑回归,如果我们已知权重μ,我们可以用下面的方式解:
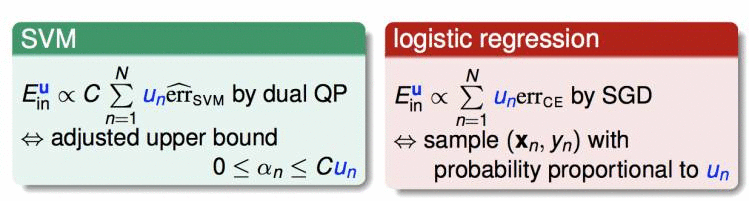
然后是第二个问题,依据什么原则来取样?或者说,怎样选择权重μ。
答案是多样性。即保证生成的每个弱分类器的差别越大,最后的聚合出来的强分类器就会越好。
如何来保证这一点呢?假设我的第t次取样生成了gt,第t+1次取样生成了g(t+1),取样的规则分别是μt和μt+1。即:
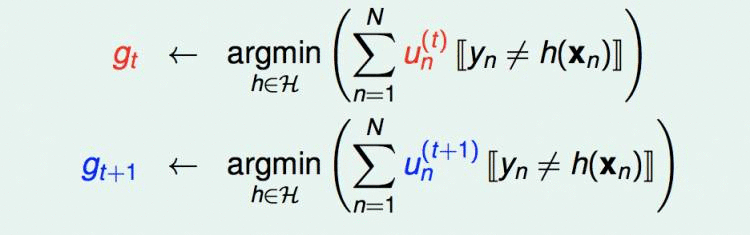
那么,要保证gt+1和gt有很大不同,有一个办法,就是使gt用在gt+1的数据集上时,效果很差。效果很差就是错误率是0.5,跟扔硬币一样:
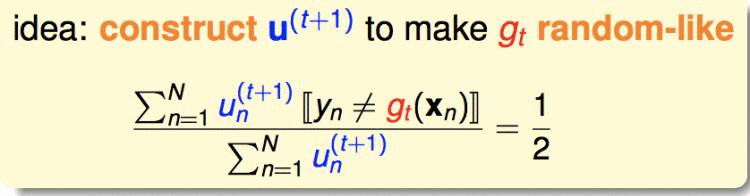
即:

所以,更新这个权重的方法是,对于t轮上分类错误的点,它的u应该更新为乘以总的分类正确率,对于分类正确的点,它的u应该更新为乘以总的分类错误率,注意这里的分类错误率是加权后的分类错误率(或者说在采样后的分类错误率):

这里我们使用另一种与上面等效的方法:

它有一定的物理意义:由于上一轮错误率总是小于0.5,因此方块t是大于1的。因此对于上一次分类正确的权重,除以方块t,减小了权重;对于上一次分类错误的权重,乘以方块t,放大了权重。
类似于水果课堂中老师教学生的例子。
第三个问题,得到了这些弱分类器,如何把他们聚合起来?AdaBoost使用的是Linear Blending的方式,其中的权重应该与方块t成正比,即这个弱分类器表现越好,权重应该越大:
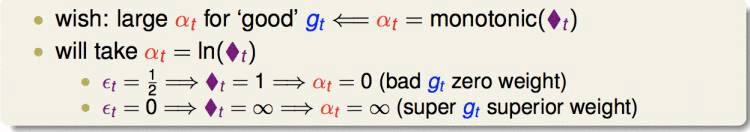
另外,初始的u我们定为均匀的。
这样,AdaBoost算法如下:

2 AdaBoost的理论保证











 京公网安备 11010802041100号
京公网安备 11010802041100号