张量是一种表示物理量的方式,这个方式就是用基向量与分量组合表示物理量(Combinationof basis vector and component)。

由于基向量可以有丰富的组合,张量可以表示非常丰富的物理量。此外,张量所描述的物理量是不随观察者或者说参照系而变化的,当参照系变化时(其实就是基向量变化),其分量也会相应变化,最后结果就是基向量与分量的组合(也就是张量)保持不变。这一点对于我们构造数据对象,进而展开分析建模,有着至关重要的意义。
回顾过去我们对“量”的认识过程,我们都懂得用“一个数”来表示数量(标量),用“一个数组”(列矩阵或行矩阵)来表示一个向量,这都属于代数手法。如果采用几何手法,标量中的实数可以表示为一维坐标系(如数轴)上的一个点,复数可以表示为二维坐标系(如复平面)上的一个点。向量通常可以表示为二维、三维或更高维坐标系中的一个空间点或有向线段。如果我们把代数手法和几何手法结合起来即采用解析几何的手法,向量又可以表示为某种坐标基向量和坐标分量的线性组合。
那么现在,我们接触的张量该如何表示呢?让我们逐“阶”而上,看看张量的数据结构形象
1、一阶张量(向量)
不妨首先假定在三维空间中,则一个一阶张量(向量)有3个分量,可以表示为一个有序3元数组或1×3阶的行矩阵
Tj = [T1 T2 T3]
在n维空间中,一个一阶张量(向量)有n个分量,可以表示为一个有序n元数组,或表示为一个1×n阶行矩阵
Tj = [T1 T2 ...... Tn]
也就是说,一个一阶张量(向量)可以用一个行矩阵表示,似乎构成“一条直线”。
2、二阶张量
在三维空间中,一个二阶张量则有9个分量,可以表示为一个有序9元数组或3×3阶的矩阵
一般地,在n维空间中,一个二阶张量有n2个分量,可以表示为一个有序n2元数组,或表示为一个n×n阶矩阵
也就是说,一个二阶张量可以用一个矩阵表示,似乎构成“一张平面”。如下图所示: 图:二阶张量矩阵平面
3、三阶张量
在三维空间中一个三阶张量
有27个分量,似乎可以构成一组3个矩阵,每个矩阵都是3×3个元素。设想“三张平面”构成一个“立方体”。如下图所示:
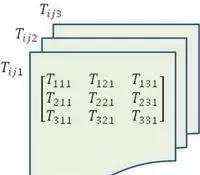
图1:三阶张量数据
如果在n维空间,一个三阶张量
有n^3个分量,也可以构成n个矩阵,每个矩阵都是n×n个元素。设想“n张平面”构成一个“立方体”,好像一块积木。如下图所示:
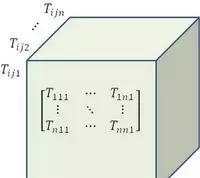
图2:三阶张量立方体积木
4、四阶张量
继续探讨我们的“积木游戏”。在三维空间中一个四阶张量
有81个分量,似乎可以构成一组9个矩阵,每个矩阵都是3×3个元素。设想每“三张平面”构成一个“立方体”,共有3个“立方体”或曰3块“积木”。3块“积木”排成一列,好像由矩阵构成的“阵列”。
如果在n维空间,一个四阶张量
有n^4个分量,也可以构成n^2个矩阵,每个矩阵都是n×n个元素。设想每“n张平面”构成一个“立方体”(一块积木),n块积木排成一列。我们把这样相互关联的一组矩阵叫做“阵列”。如下图所示:
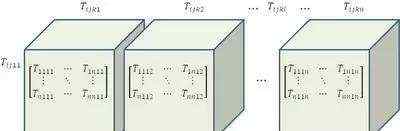
图3:四阶张量数据阵列
5、五阶张量
如果是n维空间中的一个五阶张量
,共有n^5个分量,则可以构成n^3个矩阵。设想每n张平面(矩阵)构成一块积木,每n块积木构成一条阵列,共有n条阵列,可以垒成“一堵墙”。假如以元素(张量的分量)为单位,这堵“墙”的高和长都是n^2,厚度是n。以3维空间为例,如下图所示:
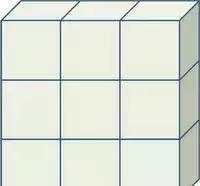
图4:五阶张量阵列墙(设n=3)
6、六阶张量
对于6阶张量,n^6个分量可以组成n^4张矩阵平面,构成n^3块积木,再排成n^2条阵列,垒成n堵墙,最后拼成一个方垛。以3维空间为例,如下图所示:
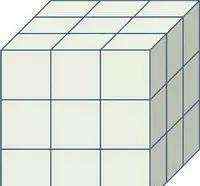
图5:六阶张量数据方垛(设n=3)
7、M阶张量
一般地,在n维空间中的一个M阶张量共有个分量,可以组成 张矩阵平面,构成 块积木,再排成 条阵列,垒成 堵墙,最后拼成 个方垛,再排成 条方垛阵列,......依此类推。
我的天啊!太恐怖啦!不要怕,计算机最擅长作这类数据结构的运算和处理。这就是在计算机时代的今天为什么要研究和普及张量算法的原因。
1.张量的四种定义
1.张量是多维数组,这个定义常见于各种人工智能软件。
2.张量是某种几何对象,不会随着坐标系的改变而改变
3.张量是向量和余向量(covector)通过张量积(tensor product)组合而成的。
4.张量是多重线性映射,即:
除零阶张量外,张量的具体表示还与坐标系的选择有关,选择不同的坐标系,意味着选择不同的基矢(basis)进行展开。以矢量为例,在给定坐标系,矢量由多个数构成,这些数实际上为当前基矢下的展开系数,如果坐标轴变化了,即基矢变化了,那么自然而然,对应的展开系数也就变化了。
2.张量表示形式
一阶张量可以理解为一个向量,二阶张量可以理解为矩阵,三阶张量可以理解成立方体,四阶张量可以理解成立方体组成的一个向量,五阶张量可以理解成立方体组成的矩阵,依次类推。
把三维张量画成一个立方体:
3.现实世界中的数据张量
1)向量数据
2D张量,形状为(samples,features)
2)时间序列数据或序列数据
3D张量,形状为(sampels,timesteps,features)
当时间(或序列顺序)对于数据很重要时,应该将数据存储在带有时间轴的3D张量中。每个样本可以被编码为一个向量序列(即2D张量),因此一个数据批量就被编码为一个3D张量。
图像通常具有三个维度:高度,宽度和颜色深度。虽然灰度图像(比如MNIST数字图像)只有一个颜色通道,因此可以保存在2D张量中,但按照惯例,图像张量始终是3D张量,灰度图像的彩色通道只有一维。因此,如果图像大小为 256 × 256 256\\times256256×256 ,那么128张灰度图像组成的批量可以保存在一个形状为(128,256,256,1)的张量中,而128张彩色图像组成的批量则可以保存在一个形状为(128,256,256,3)的张量中。
图像张量的形状有两种约定:通道在后(channels-last)的约定(在 TensorFlow 中使用)和 通道在前(channels-first)的约定(在 Theano 中使用)。Google 的 TensorFlow 机器学习框架将 颜色深度轴放在最后:(samples, height, width, color_depth)。与此相反,Theano 将图像深度轴放在批量轴之后:(samples, color_depth, height, width)。如果采 用 Theano 约定,前面的两个例子将变成 (128, 1, 256, 256) 和 (128, 3, 256, 256)。 Keras 框架同时支持这两种格式。
3)图像
4D张量,形状为(samples,height,width,channels)或(samples,channels,height,width)
4)视频
5D张量,形状为(samples,frames,height,width,channels)或(samples,frames,channels,height,width)
视频数据是现实生活中需要用到 5D 张量的少数数据类型之一。视频可以看作一系列帧, 每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_ depth) 的 3D 张量中,因此一系列帧可以保存在一个形状为 (frames, height, width, color_depth) 的 4D 张量中,而不同视频组成的批量则可以保存在一个 5D 张量中,其形状为 (samples, frames, height, width, color_depth)。
4)阶(order/ways/modes/rank)
阶:张成所属张量空间的向量空间的个数
一阶张量(向量):[5,10,15,30,25]
二阶张量(矩阵):([[5,10,15,30,25],[20,30,65,70,90],[7,80,95,20,30]])
三阶张量:([[[5,10,15,30,25],[20,30,65,70,90],[7,80,95,20,30]],[[3,1,1,0,2],[2,3,5,7,9],[7,8,5,2,3]],[[15,0,5,0,5],[0,0,5,0,0],[7,0,5,0,0]]])
在实际的操作中,秩可以理解为[的深度。例如:
rank = 1:[0,1,2]
rank = 2:[[0,1],[2,3]]
rank = 3:[[[0,1],[2,3]],[[4,5],[6,7]]]
一阶张量(向量):
二阶张量(矩阵):
三阶或更高阶张量:
零阶张量(数量):
以三阶张量为例: