IEEE754浮点数存储形式

IEEE754浮点数的表示形式

如&＃xff1a;

• 值&＃xff1a;&＃xff08;-1&＃xff09;X&＃xff08;1.M&＃xff09;X2^E-1234
• S&＃xff1a;表示符号位&＃xff0c;表示整个数的符号位
• E&＃xff1a;表示阶码&＃xff0c;注意阶码采用移码的方式&＃xff0c;没有符号位&＃xff0c;
• M&＃xff1a;表示尾码&＃xff0c;采用原码表示&＃xff0c;为了规范化&＃xff0c;尾码的最高位是有效数字1后面的数&＃xff0c;如机器原码&＃xff1a;0.000 1010 0100&＃xff0c;表示成对应的原码&＃xff0c;应该将小数点移到从左往右第一个1的后面&＃xff0c;同时将第一个1省略
  • M开头是小数点后第一位&＃xff0c;后面不都的用0补齐

移码的求法

移码是在原码的基础上加上一个偏置量&＃xff0c;确保新的二进制码便于直观的进行比较。
如

• 负数&＃xff1a;-100 0010&＃xff0c;转换成补码&＃xff1a;1011 1110
• 正数&＃xff1a;&＃43;100 0010&＃xff0c;转换成补码&＃xff1a;0100 0010&＃xff0c;
• 上述两个数对于计算机来说不易进行大小判定&＃xff0c;&＃xff0c;所全部加上偏置量1000 0000
• 负数的补码&＃xff1a;1011 1110 对应的移码0011 1110
• 正数的补码&＃xff1a;0100 0010 对应的移码1100 0010
• 上述两个数仅仅考虑数值部分&＃xff0c;不需要考虑符号位&＃xff0c;正数就比负数大。
• 求由原码求补码的快速方法
  * 原码》》补码&＃xff1a;除符号位不变&＃xff0c;全部取反&＃xff0c;末位加1
  * 补码》》移码&＃xff1a;符号位取反&＃xff0c;其余不变
  * 原码》》移码&＃xff1a;全部取反&＃xff0c;末位加1

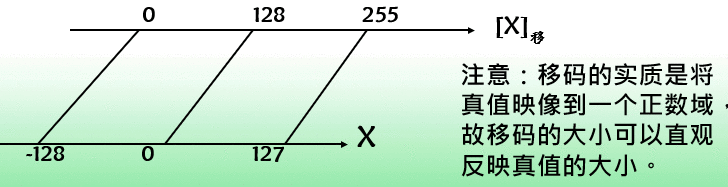
• 注意&＃xff1a;IEEE754求的移码,是在原补码的基础上加上2ⁿ - 1,以IEEE754的短浮点数为例&＃xff0c;总共有8位阶码&＃xff08;原来用补码表示&＃xff09;&＃xff0c;统一加上0111 1111&＃xff08;2⁷ - 1&＃xff09;,原先的阶码8位&＃xff0c;去掉一个符号位&＃xff0c;总共七位数&＃xff0c;表示范围-126 ~ &＃43;127&＃xff08;去掉一个0&＃xff09;&＃xff0c;加上偏置量表示范围&＃xff1a;1 ~ 254

特殊值的判定

• 无穷&＃xff1a;阶码最大&＃xff0c;全为1&＃xff0c;&＃xff08;根据移码的生成方法&＃xff0c;是在原码上全部加上一个偏置量&＃xff0c;并没有像补码一样将0和1倒置&＃xff09;&＃xff0c;尾数全为0。
• 0&＃xff1a;阶码最小&＃xff0c;全为0&＃xff0c;尾数全为0。

考试题——将一个十进制数转换为32单精度型的浮点数

写出1056.75保存为浮点数时的格式

• 将1056.75转换成对应的二进制编码&＃xff0c;整数部分和小数部分分开转&＃xff0c;然后进行合并&＃xff0c;结果为&＃xff1a;0100 0010 0000 . 1100

• 将小数点移到最高位后面一位&＃xff0c;总共移了10位&＃xff0c;将最高位的1省略&＃xff0c;前面用0补齐
  

• 阶码10的二进制编码&＃xff08;补码形式&＃xff09;&＃xff1a;0000 1010&＃xff0c;加上偏置量0111 1111&＃xff0c;结果为1000 1001

  • 注意&＃xff1a; 阶码的机器字长是8位&＃xff0c;最高位是符号位&＃xff0c;求移码是在补码的基础上加上偏置量
    

• 确定符号位&＃xff1a;结果为正数&＃xff0c;0

• 最终的浮点数编码&＃xff1a;0 1000 1001 0000 1000 0011 0000 0000 000

• 如果不强求过程&＃xff0c;可直接登录网站输入相关的数字直接获取对应的浮点数格式
• 网址&＃xff1a;https://www.h-schmidt.net/FloatConverter/IEEE754.html