作者:桃花救赎 | 来源:互联网 | 2023-08-31 21:34
原理
一组DP状态,其实等价于一个向量。而DP状态的转移方程,可以是对一个向量做变形的矩阵。那么本质上从1个向量到另一个状态的向量,是可以通过一个矩阵来做到。矩阵具有结合律,我们可以先对右半部分矩阵用快速幂得到一个终极的变形矩阵,再乘以向量,就可以把O(N)O(N)O(N)的计算 优化到 O(log(N))O (log(N))O(log(N))
示例
以大家最熟悉的斐波那契数列为例:
递推公式为 dp[i]=dp[i−1]+dp[i−2]dp[i] = dp[i-1] + dp[i - 2]dp[i]=dp[i−1]+dp[i−2],那么每一个新的数的计算依赖于前2个数,所以可以构建这么一个向量为 (dp[n−1],dp[n−2])(dp[n-1], dp[n-2])(dp[n−1],dp[n−2]),那么它和递推的下一组(dp[n],dp[n−1])(dp[n], dp[n-1])(dp[n],dp[n−1])有什么关系呢?
- dp[n]=dp[n−1]∗1+dp[n−2]∗1dp[n] = dp[n-1] *1+ dp[n - 2]*1dp[n]=dp[n−1]∗1+dp[n−2]∗1
- dp[n−1]=dp[n−1]∗1=dp[n−1]∗1+dp[n−2]∗0dp[n-1] = dp[n-1]*1=dp[n-1] *1+ dp[n - 2]*0dp[n−1]=dp[n−1]∗1=dp[n−1]∗1+dp[n−2]∗0
转换为矩阵形式,显而易见: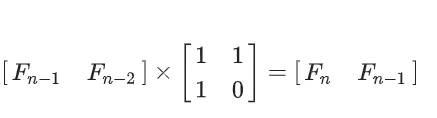
依次递推,要从 dp[2],dp[1]dp[2], dp[1]dp[2],dp[1]求到 dp[n],dp[n−1]dp[n], dp[n-1]dp[n],dp[n−1] 中间需要有n-2个同样的变形矩阵的乘法

(此处若n比较大,则需要结合矩阵快速幂优化)
传送门:矩阵快速幂优化
注:
本文部分引自西部小笼包https://www.jianshu.com/p/9817cf3c2fd9