范围搜索（kDTree）

范围搜索是从拥有多个属性的报表集合中，寻找具有特定属性且位于指定范围内的元素，这类问题被称为范围搜索。

我们在这里要解决的是二维的范围搜索问题。

在二维平面上给出一堆点，然后给出n个矩形框。要求输出在矩形框内的所有点的id。

kDtree其实就类似于二叉搜索树（嗯其实差不多就是二叉搜索树）。

题目是 DSL_2_C

我们需要建立2DTree，那就需要对x轴和y轴分别进行排序。实现方式就是，深度为偶数的时候以x轴为基准，深度为奇数时，以y轴为基准。

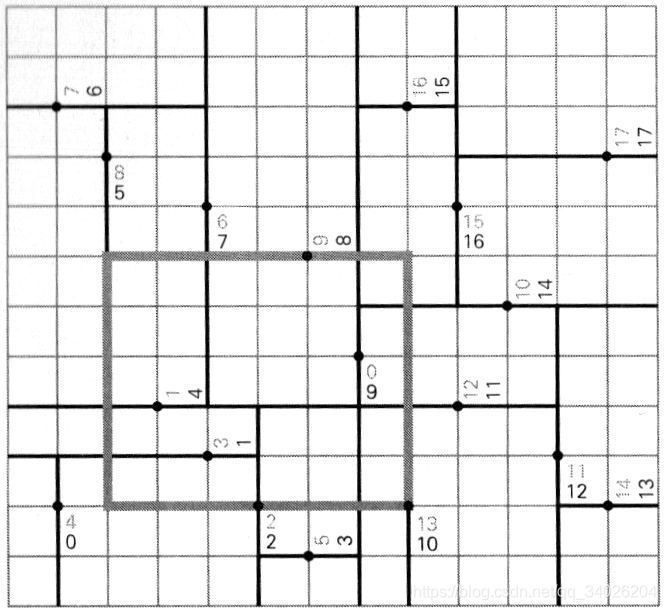
其实这就是二维分割，可以看作是把对一块大的平面区域进行分割，分别按照x轴和y轴来切一刀，接着对于每个小区域都执行相同的分割。所有的点都在分割边上的时候，停止分割。分割其实就是建立了一个类似于二叉搜索树的东西。

上代码！

#include
#include
#include
#include
using namespace std;#define MAXN 500005struct node
{int parent, left, right;int location; //对应point数组里面的元素的下标
};class point
{
public:int id, x, y;point() {}point(int id, int x, int y){(*this).id = id;(*this).x = x;(*this).y = y;}bool operator<(const point &p) const{return id };int n;
point p[MAXN];
node nd[MAXN];
int node_counter = 0;
const int NIL = -1;bool cmpX(const point &a, const point &b)
{return a.x }bool cmpY(const point &a, const point &b)
{return a.y }int make2Dtree(int left, int right, int depth)
{if (left >= right)return NIL;int t = node_counter++;if (depth % 2 == 0) //以x为基准对p升序排序{sort(p + left, p + right, cmpX);}else{sort(p + left, p + right, cmpY);}int mid = (left + right) / 2;nd[t].location = mid;nd[t].left = make2Dtree(left, mid, depth + 1);nd[t].right = make2Dtree(mid + 1, right, depth + 1);return t;
}vector

ans;void search(int u, const int &sx, const int &tx, const int &sy, const int &ty, int depth)
{int x = p[nd[u].location].x;int y = p[nd[u].location].y;if (x >= sx && x <= tx && y >= sy && y <= ty){ans.push_back(p[nd[u].location]);}if (depth % 2 == 0){if (nd[u].left != NIL){if (sx <= x)search(nd[u].left, sx, tx, sy, ty, depth + 1);}if (nd[u].right != NIL)if (x <= tx)search(nd[u].right, sx, tx, sy, ty, depth + 1);}else{if (nd[u].left != NIL)if (sy <= y)search(nd[u].left, sx, tx, sy, ty, depth + 1);if (nd[u].right != NIL)if (y <= ty)search(nd[u].right, sx, tx, sy, ty, depth + 1);}
}int main()
{scanf("%d", &n);int x, y;for (int i = 0; i }

转载请注明原文链接：https://www.longjin666.top/?p=752