作者:小小号号-- | 来源:互联网 | 2023-10-12 18:39
首先介绍点基础知识,另一方面也算是巩固下:
A−1表示A的逆矩阵;
AT表示A的转置;
AH表示Hermitian矩阵(A的共轭转置矩阵A∗==A)
基础
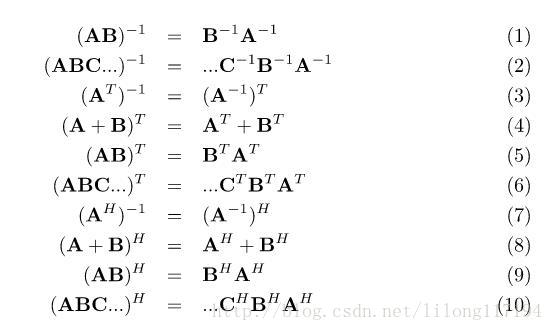
(1)迹(Trace)
eig(A)表示A的特征值
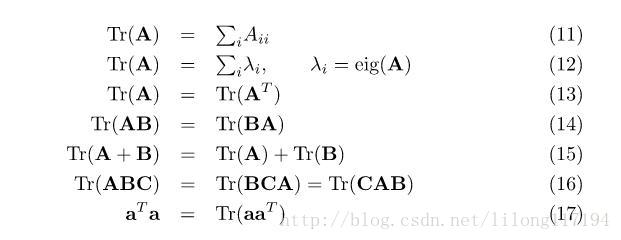
(2)行列式(Determinant)
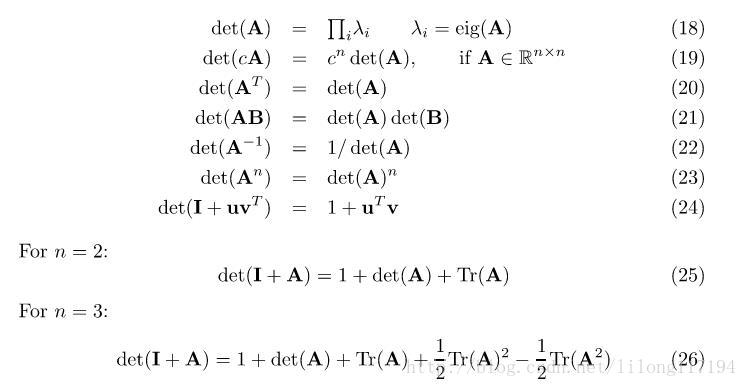
(3)特例2*2矩阵

以上是摘自:The Matrix Cookbook
也可参考维基百科:Matrix calculus
L1范数的次微分
L1范数不可微。但是存在次梯度,即是次微分的
L1范数的次梯度如下:
∂∂x||x||1=sign(x)
其中sign(x) 表示如下:
sign(x)&#61;⎧⎩⎨⎪⎪&#43;1−1[−1,1]xi>0xi<0xi&#61;0
而
L1范数&#xff1a;
||X||1&#61;|x1|&#43;|x2|&#43;⋯&#43;|xn|
例如&#xff1a;
x&#61;(3,2,−5)T 故其梯度为&#xff1a;sign(x)&#61;(1,1,-1)
L2范数的微分

例如&#xff1a;求解下面函数的偏导数&#xff1a;
f(W)&#61;12∑i,jϵSγi,j||wTiX−wTjX||22
得&#xff1a;
∂f(W)∂wi&#61;∑i,jϵsγi,j(wTiX−wTjX)∗∂(wTiX−wTjX)∂wi&#61;∑i,jϵsγi,j(wTiX−wTjX)∗XT&#61;∑i,jϵsγi,j(wTi−wTj)∗(XXT)
注意这里得到的是行向量的形式&#xff0c;因此还需要对其进行转置
以上的推倒是基于上图公式得到。。。