定位导航——旋转矩阵，IMU，左右乘

我们先明确一下这里所说的一些概念

IMU

IMU全称Inertial Measurement Unit，惯性测量单元，主要用来检测和测量加速度与旋转运动的传感器。起初只是用来测量角度的，后来随着其他传感器的加入，它的功能变得多样了，而很多情况下，其名称还是IMU，因此这也导致了：有的人认为IMU只能计算一些惯性力，进而获得旋转角度（加速度计）；有些人发现有些叫IMU的产品还可以算偏航角（加速度计+磁力计）；而更有甚者，IMU居然还能获得经纬度（加速度计+磁力计+GNSS）

1）IMU包含加速度计和磁力计
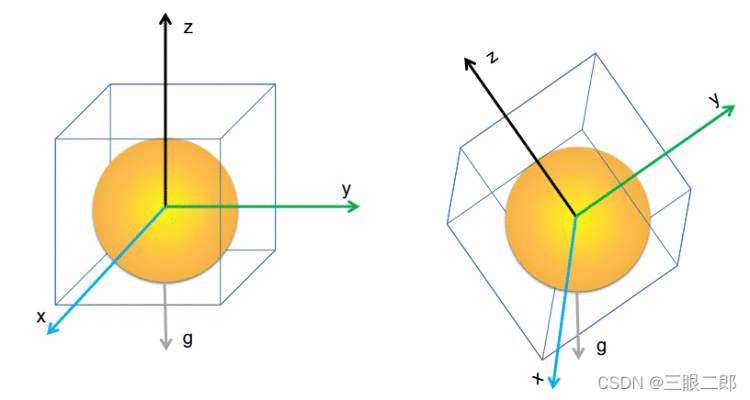
我们先设想，我们的加速度计是一个正方体，里面放置一个小球。初始状态是平方放在桌面，重力加速度g是垂直于平面的，即四周没有受力，其实我们的IMU没有绕x轴和y轴旋转。当我们绕x轴旋转后，我们会看到g被分摊到两个平面，原本不受力的垂直于y方面的平面有了一个力，原本垂直于z方面的平面由原来的受力g变为了小于g的力。
通过这些力的分析，我们就可以算出我们的倾角。
这里记住，加速度计并非是我们来计算我们运动物体的加速度，而是在物体匀速运动或者静止时，我们通过算出重力对受力平面的影响进而算出角度。
这里还要注意，偏航角定义为x轴投影到g垂直的平面后，与北方向的夹角，因此该角度和g无关，即加速度计无法获得偏航角。

俯仰角，横滚角，yaw角：来自加速度计
偏航角：磁力计

这里要注意，偏航角已经涉及了本体与地球北方向的夹角，即
如果你单纯研究机体，那么你不用偏航角，不用磁力计
如果你还需要把机体搞到大地坐标系，那么你需要偏航角

2）厂家为其集成了GNSS
GNSS（全球导航为习惯系统），可用于提供高经纬度信息
这里还涉及了一个坐标系转换的考虑
IMU坐标系的坐标原点在其质心
GNSS坐标系的坐标原点在其天线（蘑菇头）的中心位置
所以如果给IMU集成GNSS，需要将GNSS天线坐标系下获得的经纬度转换到IMU坐标系，以实现整体的统一。

旋转矩阵

首先我们先明确我们为什么要用旋转矩阵
因为旋转一个角度，它的旋转结果只有一种
但是旋转两个角度，它们的组合就会出现两种
R1R2；R2R1
如果三个角度，则会出现更多
一般情况下，三维的旋转矩阵是不满足交换律的，先绕哪个轴转，再绕哪个轴转，结果是不一样的

直接拿我们的俯仰，横滚和偏航为例，这三个角度，都是我们的机体坐标系与参考坐标系（大地坐标系）的夹角，这三个夹角都有明确的定义，和是我们自己想，我们会发现，这些角度的定义都是绕着机体坐标系定义的，而并非是参考坐标系。
俯仰：以飞机的翅膀为轴
横滚：以飞机的头为轴
偏航：飞机的航向与北方向的夹角

？？？？？，前两个角都是以飞机为参考的，最后一个不是了？？？
其实这里定义的挺乱的
准确来说，我们在研究姿态时，是不应该引入偏航角的，而我们要用的是yaw角

偏航角是

左乘右乘——纯属坑人，看下面就知道了

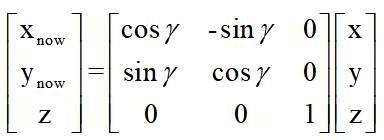
绕z旋转如上图，（x，y，z）是我们当前需要旋转的坐标系的坐标点
绕z轴旋转，z保持不变，从旋转矩阵也可以看出，它让我们的z保持不变

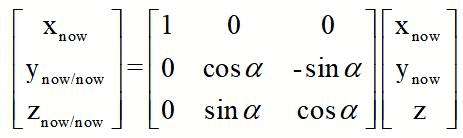
然后我们再绕xnow轴旋转，如上图，（xnow，ynow，z）是我们绕z旋转后的新坐标系下的坐标点
绕xnow轴旋转，x保持不变，从旋转矩阵也可以看出，xnow没有发生变化。

这说明了什么？乘上一个旋转矩阵，其旋转轴都是我们当前坐标系的轴。
记住，这是当前坐标系。。。。。。。。！！！！！！！！！

这样一下就通顺了，你会发现，很多公司给出的旋转矩阵都是最后再转偏航角，因为前两次旋转把当前坐标系的xy0平面转换到了与世界坐标系的XY0平面平行，这个平行成立之后，那么
偏航角直接可以绕着当前坐标系的z轴旋转了。

偏航角≠yaw

按偏航角转过来，你会发现，你的x轴指向了北
按yaw转过来，你会发现，你的x轴指向没有实际的物理意义

旋转矩阵做了什么？

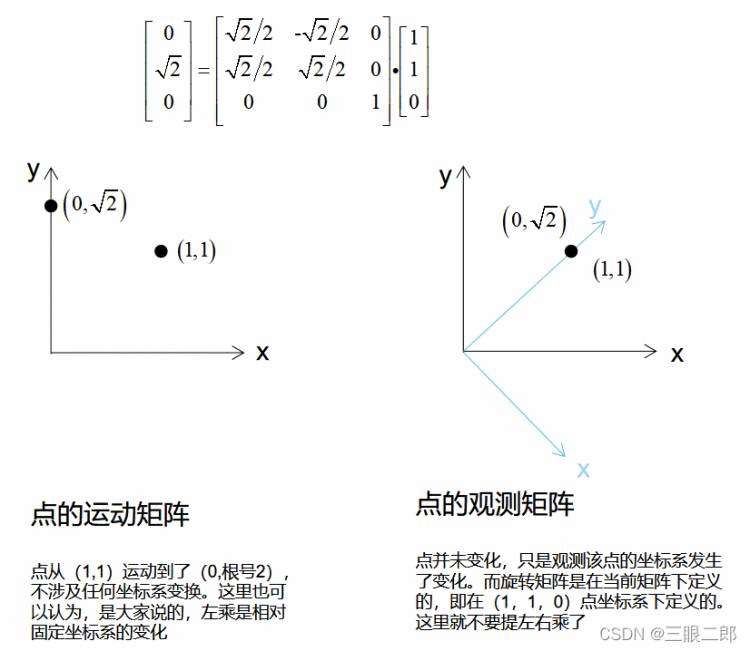
可以看到，我们的用途不同，旋转矩阵对于点的意义有所不同。

这也就是，在学习机器人运动时，我们听到的左乘为固定坐标系，右乘为变化坐标系，其实说的都是点的运动，真实的原坐标系并未发生变化，只是点动了，可能会生成新的坐标系作为新的参考，就有了右乘。

在点的观测时，我们只考虑坐标系的变化，它的变化都是绕当前坐标系转动，都是乘在左边，而并非大家说的左右乘。

这里也就好说明了，都是按照当前矩阵旋转，因此那些先转俯仰后转横滚和先转横滚后转俯仰的，两者可能结果相同，但是角度的大小肯定不一致，因此，用哪家的imu必须问清楚，其旋转矩阵怎么定义的，才能使用。

角度正负问题
正常右手坐标系，逆时针的都为正
看清商家的坐标系定义和角度定义，转换到和你自己坐标系匹配的关系，然后再求解。

关于矩阵中是-sinθ还是+sinθ，还有必要再谈一下
1）下图这一套旋转矩阵，准确来说应该是回退旋转矩阵
绕X和Z的转动都是右上角为负值
θ的正负是按如何转过来的定义


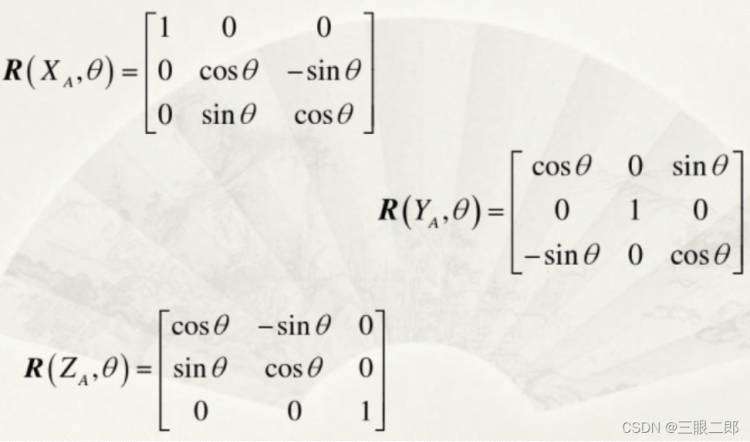
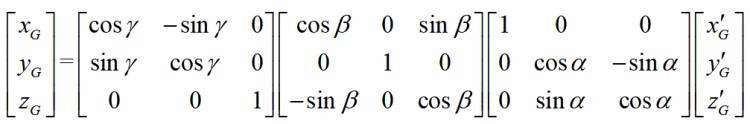
上式从左到右为惯性坐标系到物体坐标系，做了哪些旋转

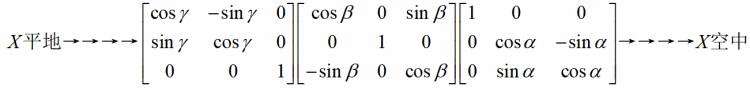
1）拿飞机为例子，平地的飞机到空中的飞机，需要如何操作。
下式可以表示为飞机先绕大地的z轴转了γ角，即飞机偏航了γ角；然后绕y轴转了β角，即飞机逆时针横滚了β角，；最后飞机绕x轴转了α角，即飞机扬起了头，扬了α角。

上式从右到左为物体坐标系回退到惯性坐标系，需要回退的步骤

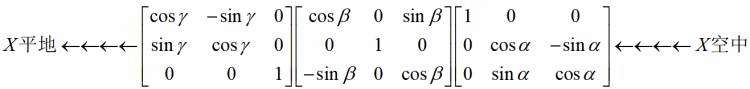
这时分清楚α、β和γ，哪个是当前坐标系定义的，很显然，飞机从地面到空中最后一次用的α角，那么从空中到地面第一个就要用该角，然后转β角，最后转γ角。
这里可能会有人异或，角度不应该是负值么，回退应该是往回转的？
这里需要明白一点

坐标点的对应：

观测的点是绝对的，它对于世界来说是不动的；
点和坐标系的关系是相对的，坐标系顺时针转，点就逆时针转。
这里转坐标系是顺时针转了α，那么点就要逆时针转α，即上式的正值。