递归函数
递归的定义
1.什么是递归&＃xff1a;在一个函数里调用这个函数本身
def foo(): print(n) n&＃43;&＃61;1 foo(n)foo(1)
2.最大递归层数限制&＃xff1a;997&＃xff0c;是python默认的&＃xff0c;可以做修改&＃xff0c;但是不建议你修改。(因为如果用997层递归都没有解决的问题要么是不适合使用递归来解决问题&＃xff0c;要么就是你的代码太烂了0.0)
import syssys.setrecursionlimit(10000000) #修改递归层数n&＃61;0def f(): global n n&＃43;&＃61;1 print(n) f()f()3.结束递归的标志&＃xff1a;return4.递归解决的问题&＃xff1a;通过参数&＃xff0c;来控制每一次调用缩小计算的规模5.使用场景&＃xff1a;数据的规模在减少&＃xff0c;但是解决问题的思路没有改变6.很多排序算法会用到递归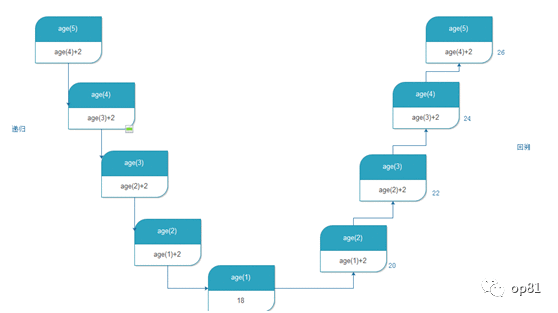
递归小应用
1.猜小明的年龄
小明是新来的同学&＃xff0c;丽丽问他多少岁了。他说&＃xff1a;我不告诉你&＃xff0c;但是我比滔滔大两岁。滔滔说&＃xff1a;我也不告诉你&＃xff0c;我比晓晓大两岁晓晓说&＃xff1a;我也不告诉你&＃xff0c;我比小星大两岁小星也没有告诉他说&＃xff1a;我比小华大两岁最后小华说&＃xff0c;我告诉你&＃xff0c;我今年18岁了
这个怎么办呢&＃xff1f;当然&＃xff0c;有人会说&＃xff0c;这个很简单啊&＃xff0c;知道小华的&＃xff0c;就会知道小星的&＃xff0c;知道小星的就会知道晓晓的&＃xff0c;以此类推&＃xff0c;就会知道小明的年龄啦。这个过程已经非常接近递归的思想了。
| 小华 | 18&＃43;2 |
| 小星 | 20&＃43;2 |
| 晓晓 | 22&＃43;2 |
| 滔滔 | 24&＃43;2 |
| 小明 | 26&＃43;2 |
上面的图我们可以用个序号来表示
age(5) &＃61; age(4)&＃43;2age(4) &＃61; age(3) &＃43; 2 age(3) &＃61; age(2) &＃43; 2age(2) &＃61; age(1) &＃43; 2age(1) &＃61; 18
那么代码该怎么写呢&＃xff1f;
def age(n): if n &＃61;&＃61; 1: return 18 else: return age(n - 1) &＃43; 2ret&＃61;age(6)print(ret)2.一个数&＃xff0c;除2直到不能整除
def cal(num): if num%2&＃61;&＃61;0:#先判断能不能整除 num&＃61;num//2 return cal(num) else: return numprint(cal(8))3.如果一个数可以整除2&＃xff0c;就整除&＃xff0c;不能整除就*3&＃43;1
def func(num): print(num) if num&＃61;&＃61;1: return if num%2&＃61;&＃61;0: num&＃61;num//2 else: num&＃61;num*3&＃43;1 func(num)func(5)
二分查找法
从这个列表中找到55的位置
l&＃61;[2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
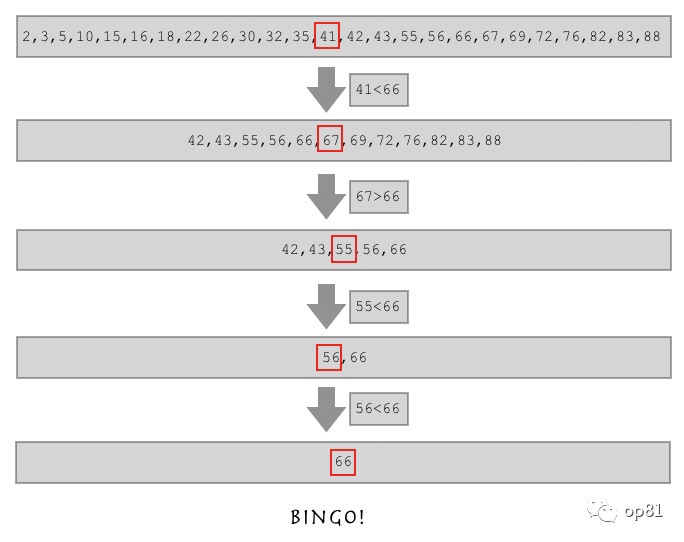
这就是二分查找&＃xff0c;从上面的列表中可以观察到&＃xff0c;这个列表是从小到大依次递增的有序列表。按照上面的图就可以实现查找了。
简单二分法
l &＃61; [2, 3, 5, 10, 15, 16, 18, 22, 26, 30, 32, 35, 41, 42, 43, 55, 56, 66, 67, 69, 72, 76, 82, 83, 88]def find(l,aim): mid&＃61;len(l)//2 #取中间值&＃xff0c;//长度取整(取出来的是索引) if l[mid]>aim: #判断中间值和要找的那个值的大小关系 new_l&＃61;l[:mid] #顾头不顾尾 return find(new_l,aim) #递归算法中在每次函数调用的时候在前面加return elif l[mid] new_l&＃61;l[mid&＃43;1:] return find(new_l,aim) else: return l[mid]print(find(l,66))
升级版二分法
l &＃61; [2, 3, 5, 10, 15, 16, 18, 22, 26, 30, 32, 35, 41, 42, 43, 55, 56, 66, 67, 69, 72, 76, 82, 83, 88]def func(l, aim,start &＃61; 0,end &＃61; len(l)-1): mid &＃61; (start&＃43;end)//2#求中间的数 if not l[start:end&＃43;1]:#如果你要找的数不在里面&＃xff0c;就return&＃39;你查找的数字不在这个列表里面&＃39; return &＃39;你查找的数字不在这个列表里面&＃39; elif aim > l[mid]: return func(l,aim,mid&＃43;1,end) elif aim 匿名函数
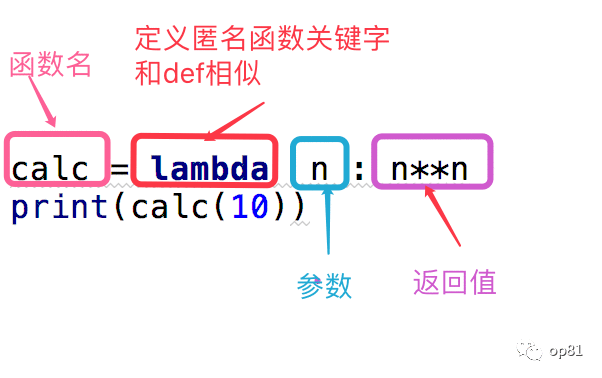
匿名函数&＃xff1a;也叫lambda表达式
匿名函数的核心&＃xff1a;一些简单的需要用函数去解决的问题&＃xff0c;匿名函数的函数体只有一行。参数可以有多个&＃xff0c;用逗号隔开。返回值和正常的函数一样可以是任意的数据类型
匿名函数练习1.函数转变为匿名函数#把下面的函数转换成匿名函数def add(x,y) return x&＃43;yadd()#结果&＃xff1a;sum1&＃61;lambda x,y:x&＃43;yprint(sum1(5,8))
2.比大小
dic &＃61; {&＃39;k1&＃39;:50,&＃39;k2&＃39;:80,&＃39;k3&＃39;:90}# func&＃61; lambda k:dic[k]# print(max(dic,key&＃61;func))print(max(dic,key &＃61; lambda k:dic[k])) #上面两句就相当于下面一句
3.map方法的应用
l&＃61;[1,2,3,4]# def func(x):# return x*x# print(list(map(func,l)))print(list(map(lambda x:x*x,l)))
4.filter函数的小应用
l&＃61;[15,24,31,14]# def func(x):# return x>20# print(list(filter(func,l)))print(list(filter(lambda x:x>20,l)))
5.现有两个元组((&＃39;a&＃39;),(&＃39;b&＃39;))&＃xff0c;((&＃39;c&＃39;),(&＃39;d&＃39;))&＃xff0c;请使用python中匿名函数生成列表[{&＃39;a&＃39;:&＃39;c&＃39;},{&＃39;b&＃39;:&＃39;d&＃39;}]
# 方法一t1&＃61;((&＃39;a&＃39;),(&＃39;b&＃39;))t2&＃61;((&＃39;c&＃39;),(&＃39;d&＃39;))# print(list(zip(t1,t2)))print(list(map(lambda t:{t[0],t[1]},zip(t1,t2))))# 方法二print(list([{i,j} for i,j in zip(t1,t2)]))#方法三func &＃61; lambda t1,t2:[{i,j} for i,j in zip(t1,t2)]ret &＃61; func(t1,t2)print(ret)
6.列表推导式
#30以内所有被3整除的数print(list([i for i in range(30) if i%3&＃61;&＃61;0]))
7.字典推导式
例一&＃xff1a;将一个字典的key和value对调
mcase &＃61; {&＃39;a&＃39;: 10, &＃39;b&＃39;: 34}res1 &＃61; {i:mcase[i] for i in mcase}res&＃61;{mcase[i]:i for i in mcase }print(res1)print(res)
例二&＃xff1a;合并大小写对应的value值&＃xff0c;将k统一成小写
mcase &＃61; {&＃39;a&＃39;:10,&＃39;b&＃39;:34,&＃39;A&＃39;:7}res &＃61; {i.lower():mcase.get(i.lower(),0)&＃43;mcase.get(i.upper(),0) for i in mcase}print(res)
8.集合推导式
例&＃xff1a;计算列表中每个值的平方&＃xff0c;自带去重功能
l&＃61;[5,-5,1,2,5]print({i**2 for i in l})
京公网安备 11010802041100号