www.bilibili.com/video/BV147411K7x...

y= x^2 - 3x +2
则 计算为
| 1*x | -1 |
|---|---|
| 1*x | -2 |
十字相乘为: (x-1)(x-2)
其中 我们必须做到 -1 + -2 = -3。
y= ax^2 - bx +c (a不等于0)
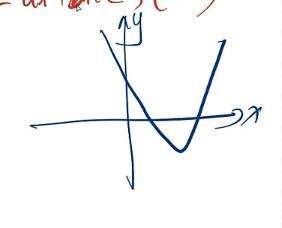
b控制 Δ(德尔塔) 与 X轴交掉
c控制 与y 的交点
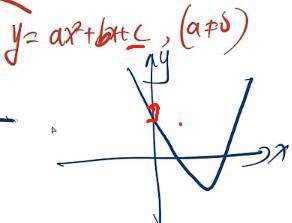
还要知道的是: a >0时,
Δ(德尔塔) = b^2-4ac
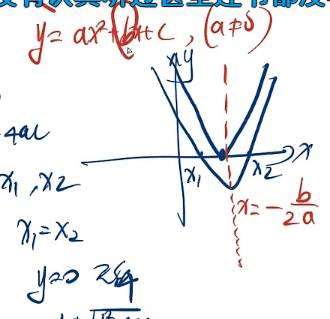
两个根 分别为 x1 x2(表示1号x,与2号x),如下图
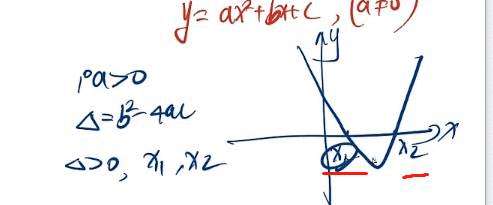
则函数与X轴 只有一个交点。那么实际上x1 x2(表示1号x,与2号x) 依然存在。只不过 x1= x2.如下图红色部分
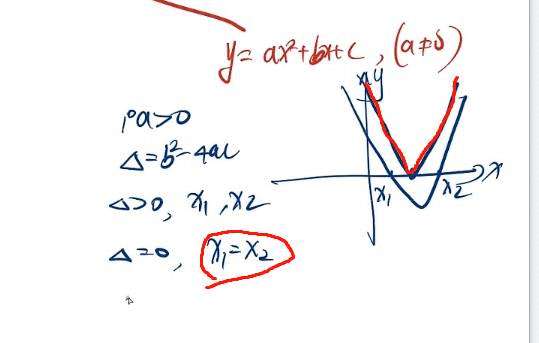
则x1 与x2 是不存在的。无解的。或者说 y=0,是无解的。
因为 Δ(德尔塔) <0的时候,他们没有交点。所以当y等于0的时候是无解的。
因为Δ(德尔塔)还控制着,交点的值是多少。
Δ(德尔塔)是求值公式得到的。
如图:公式不好打
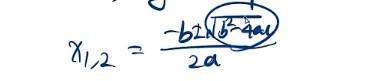
则 这里框起来的就是 Δ(德尔塔)。
这就是求根公式,此公式确定了我们与x轴的两个交点。
交点的前提条件,是 Δ(德尔塔)大于0
所有一元二次对称轴 都是 x= -b/2a

y= x^2 - 3x +2
则 计算为
| 1*x | -1 |
|---|---|
| 1*x | -2 |
十字相乘为: (x-1)(x-2)
其中 我们必须做到 -1 + -2 = -3。
y= ax^2 - bx +c (a不等于0)

b控制 Δ(德尔塔) 与 X轴交掉
c控制 与y 的交点

还要知道的是: a >0时,
Δ(德尔塔) = b^2-4ac
两个根 分别为 x1 x2(表示1号x,与2号x),如下图

则函数与X轴 只有一个交点。那么实际上x1 x2(表示1号x,与2号x) 依然存在。只不过 x1= x2.如下图红色部分
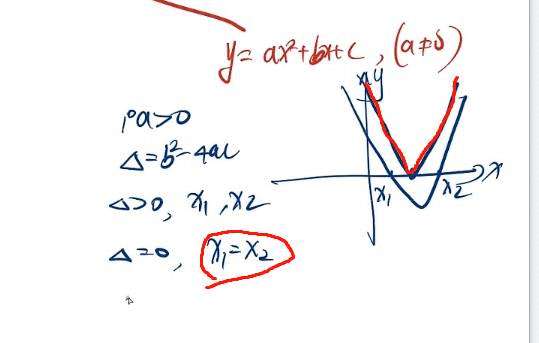
则x1 与x2 是不存在的。无解的。或者说 y=0,是无解的。
因为 Δ(德尔塔) <0的时候,他们没有交点。所以当y等于0的时候是无解的。
因为Δ(德尔塔)还控制着,交点的值是多少。
Δ(德尔塔)是求值公式得到的。
如图:公式不好打
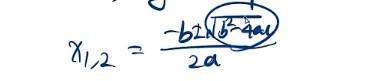
则 这里框起来的就是 Δ(德尔塔)。
这就是求根公式,此公式确定了我们与x轴的两个交点。
交点的前提条件,是 Δ(德尔塔)大于0
所有一元二次对称轴 都是 x= -b/2a
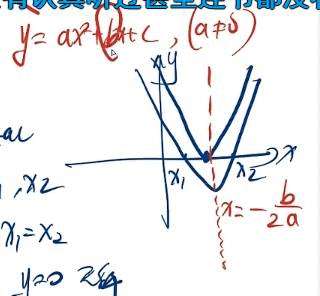
注意,当 b =0.则 x=0. 那么我们的对称轴 就是Y轴啊。
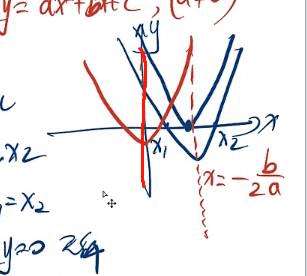
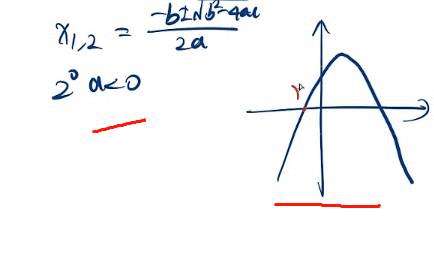
当然我们的根 对称轴 全都是一样的。
这里的 a 只控制了 开口方向
我们也可以 求
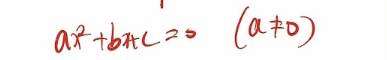
我们可以使用 十字相乘法。也可以使用,函数求根公式。
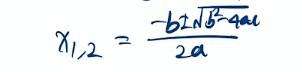
如果还是解不开,有非常复杂的求。那么就是使用韦达定理。
韦达定理=
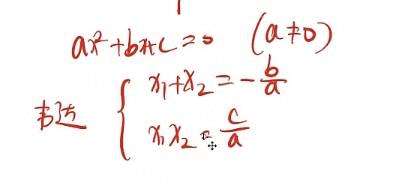
Δ(德尔塔) 大于0,则可以使用韦达定理
二次不等式很头疼。
y = x^2 - 3x +2 > 0
得到 (x-1)(x-2) >0
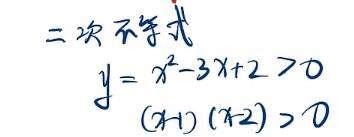
则画图,
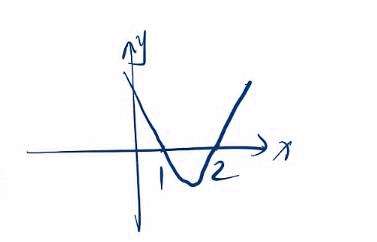
可以发现一目了然。
这时候我们记住口诀。
** 大于取两边,小于取中间。**
计算 小于等于0 。那就转化。同时注意要保证开口向上。 这样子口诀才是有效的。
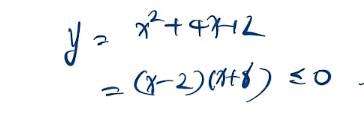
画图:
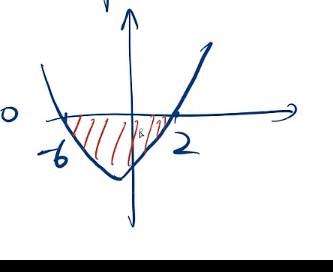
则此处,利用十字相乘法得到两个根。
再画图,得到两个根。找到小于等于0的地方。
注意 解答时候要带上等于号
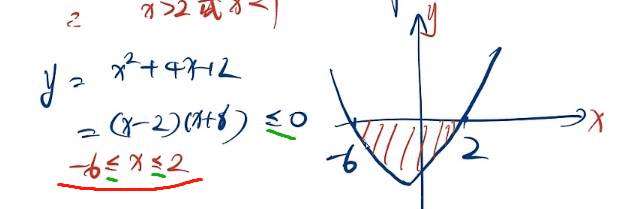

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有