【课程来源】感谢B站Up主leonding1018的分享,老师的课程内容非常精彩。
本文是观看网络视频课程后的笔记,如涉及版权问题,请及时留言或私信与我联系。
TSP问题是一个NP hard问题,在一个多项式时间内不能找到一个最优解。
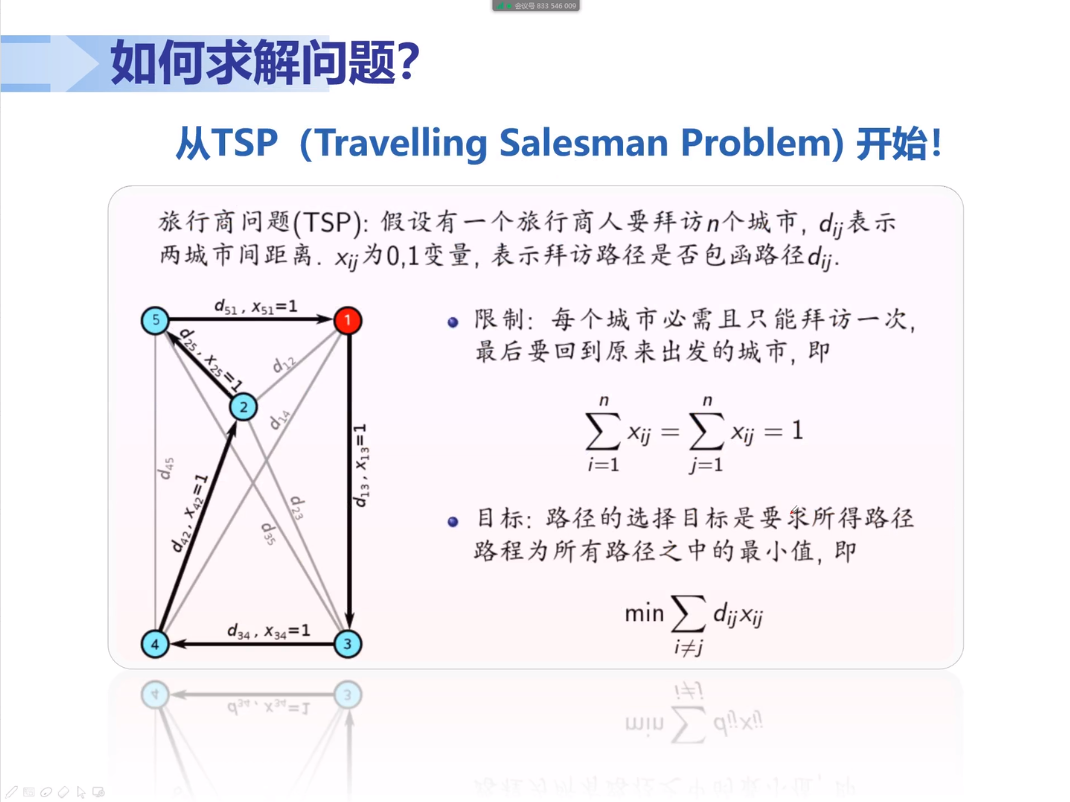
单个车辆遍历路径(TSP问题)可以扩展为:多车辆遍历路径(VRP),车辆实时路径规划,订单分配给不同车辆(调度优化),零部件排产等。
举了即时战略游戏中目标对象选择路径找过障碍物到达目的地的例子,目标是让英雄从地图左上角A点运动到右下角B点。如图所示,黑色部分为障碍物,“黄橙红”颜色标记了每一个坐标被遍历访问的此处。上方为枚举法对地图各坐标的访问频次,下方为A Star搜索方法对地图各坐标的访问频次。可以看出A Star方法只访问了较少的坐标,提高了搜索效率。

(1)从当前点(x=1,y=2)开始遍历相邻点(算出g=当前点到新点单步距离,h=新点到终点不考虑障碍物的剩余距离,f=g+h);

(2)选取f最小的点作为新的当前点(x=2,y=3);
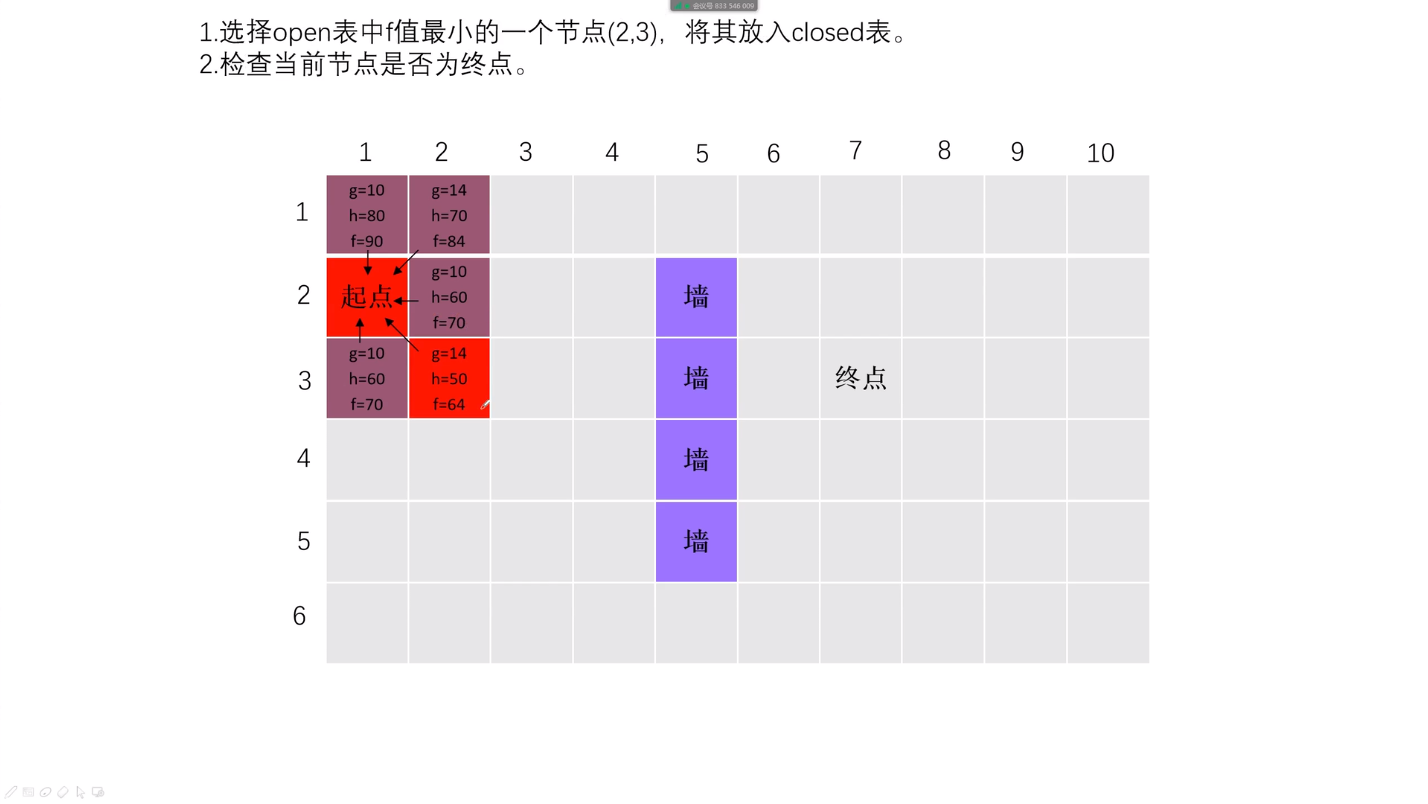
(3)重复步骤1;
(x,y)从(2,3)到(3,3)

(x,y)从(3,3)到(4,3)

(4)注意所有已探索未步入的点,都是候选点,这是便于选错路的回头纠正;
(x,y)从(4,3)回头到(1,3),再回头到(2,2)
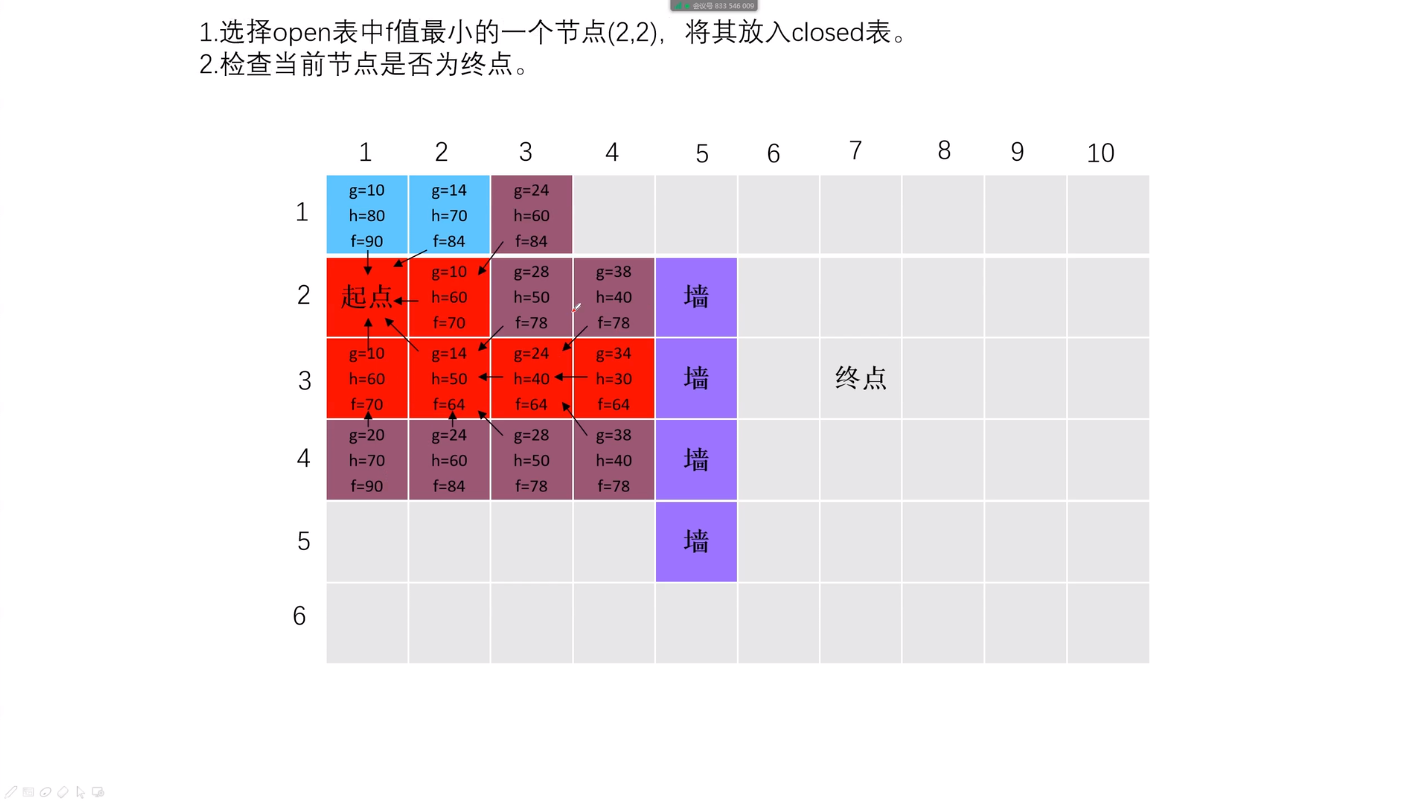
(5)当重新选取了当前节点(即回头)后,相关已探索节点的g/h/f值也应更新。
注意当前点改为(2,2)后,点(3,2)、(4,2)的g/h/f值都进行了更新。
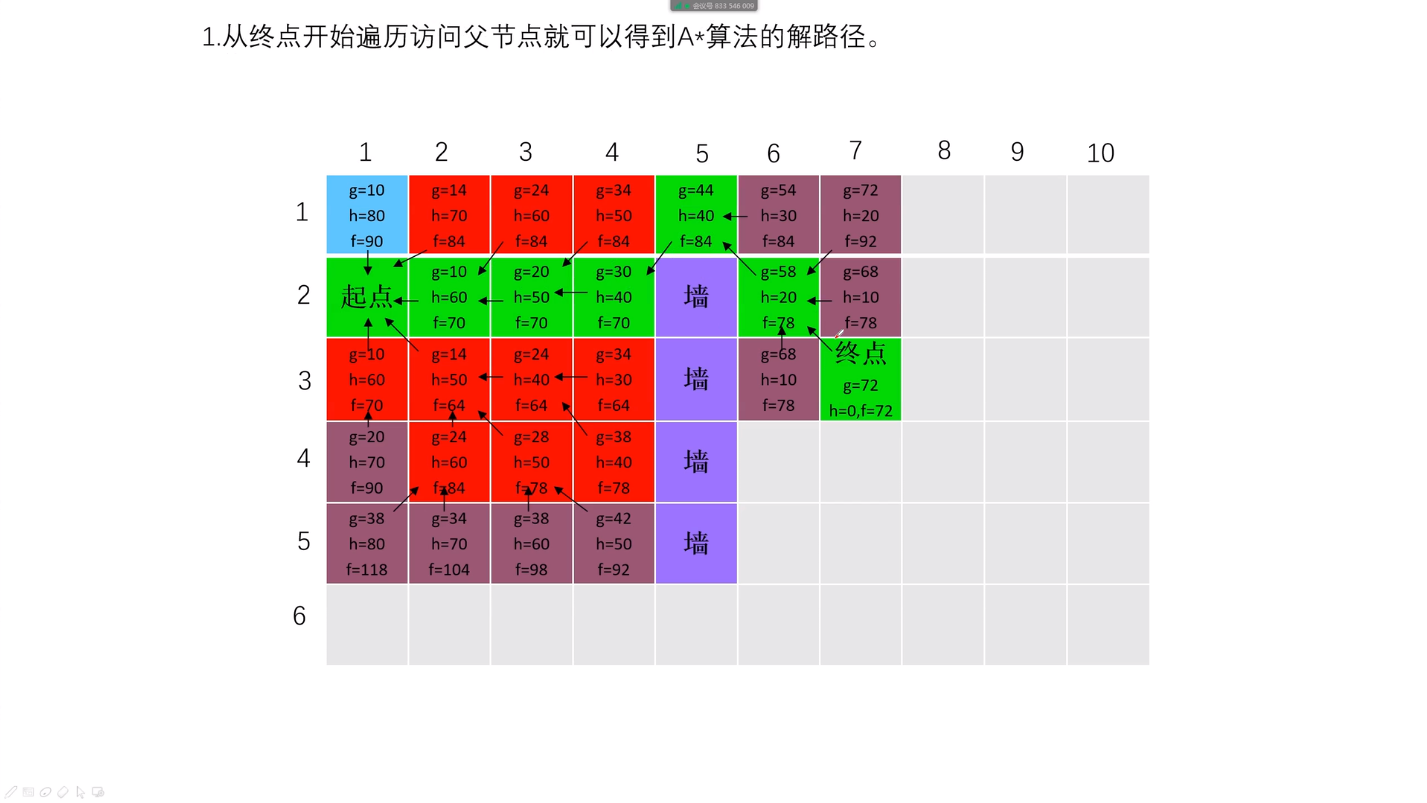
(6)注意每个新点都记录着其对应的父节点,便于最后一步回溯;
留意之前每一幅图上的箭头,当前点变化后,箭头也发生了变化。
(7)当前点移动到终点后,从终点开始,根据父节点可反推出最优路径。
上图中绿色标记的路径。
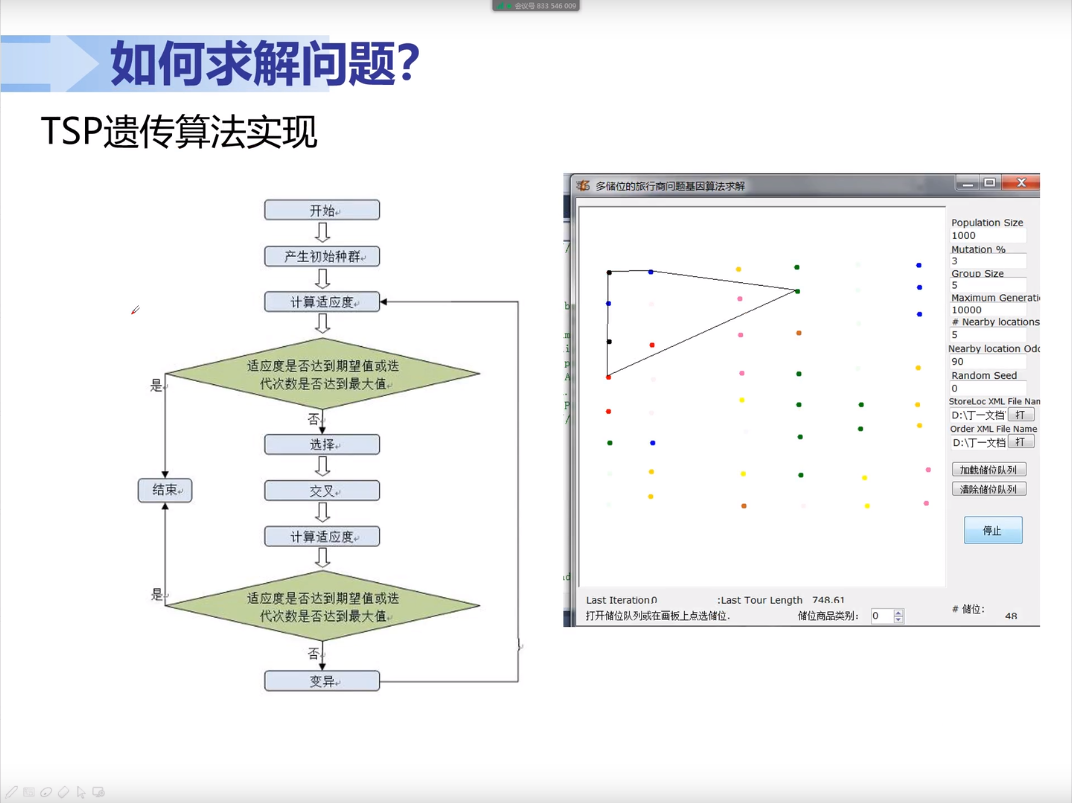
(1)先随机生成一定数量(例如1000条)的解;
(2)然后按一定比例(例如10%)选出其中较好的100个保留,其余的900条再变异;
(3)在第上一步新生成的1000条中选100个保留,其余的变异;
(4)重复步骤3若干次;
(5)选1000条中最好的一个,作为最优解。
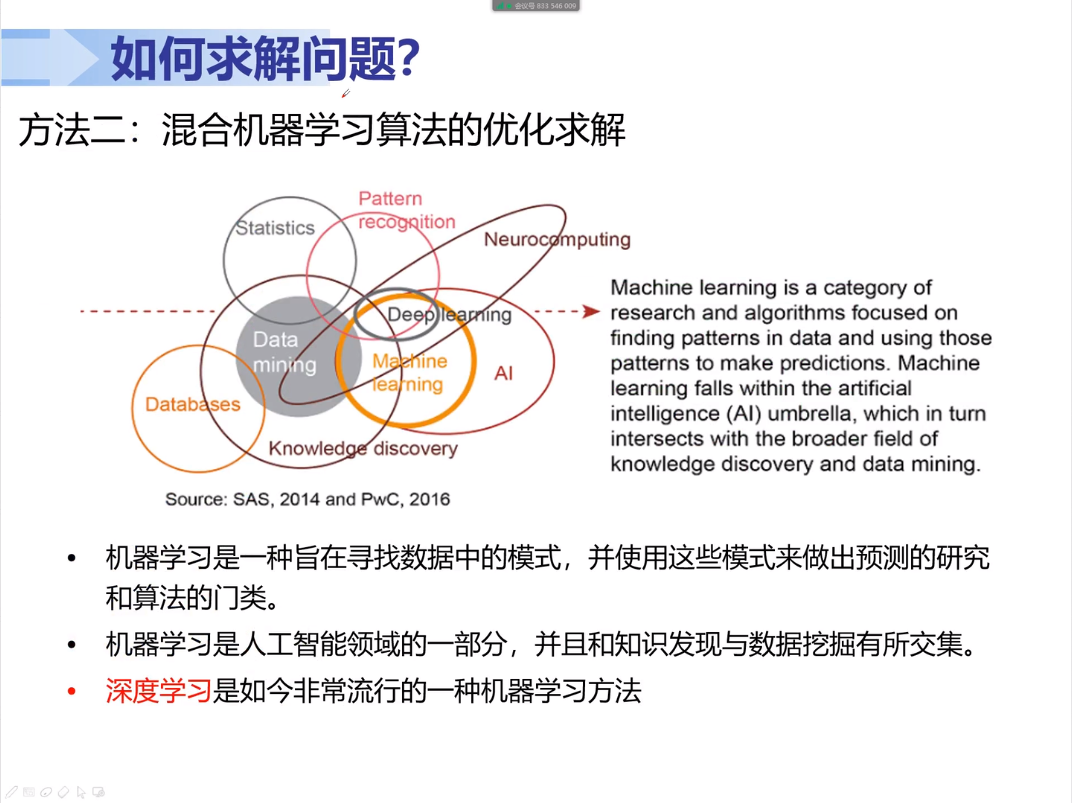
应留意图片中一些城建概念的关系,包括:数据库、指示发现、数据挖掘、统计、图形识别、神经计算、人工智能、机器学习、深度学习。比如,机器学习的范围大于深度学习,人工智能的范围大于机器学习。
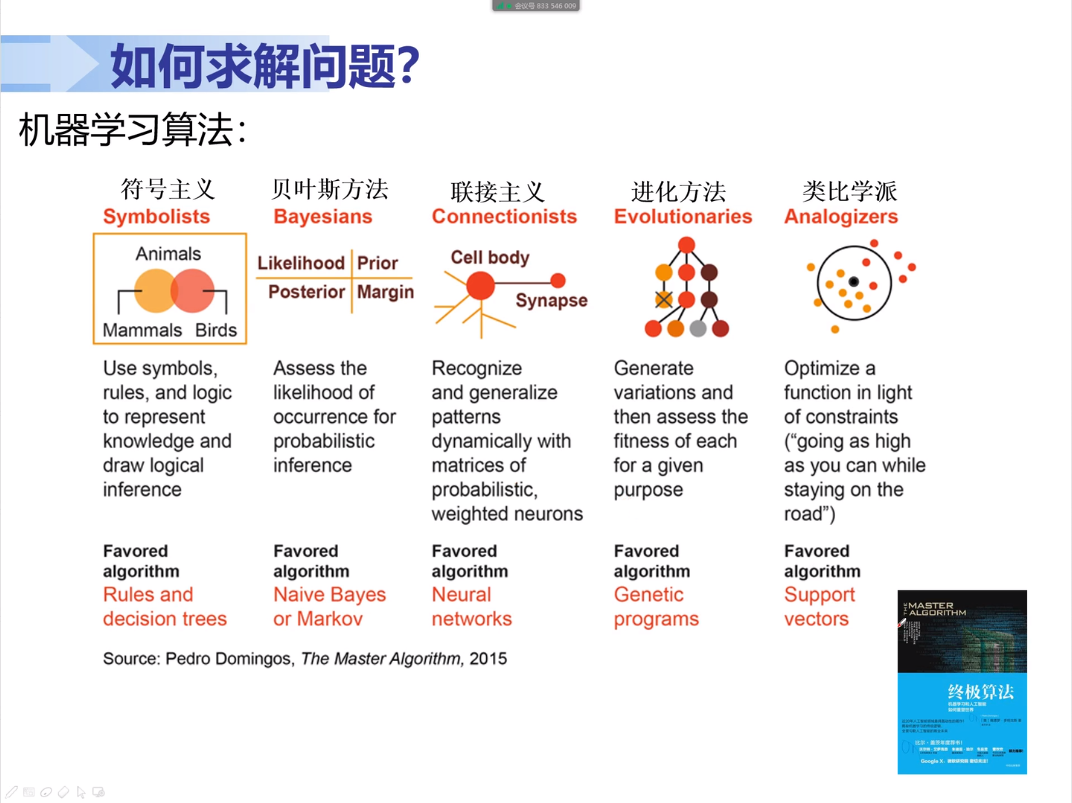
《终极算法》(推荐书)中将算法分为5大类:
(1)符号主义:通过规则和决策树进行推理;
(2)贝叶斯方法:通过统计学中的贝叶斯(先验后验)概率;
(3)联接主义:模拟人脑,创建节点和连接网络进行非线性关联,代表性有神经网络;
(4)进化方法:模拟生物进化,迭代创建新的节点,代表性有遗传算法;
(5)类比学派:利用样本特征相似性,代表性有KNN聚类分析(商品推荐)和支持向量机。
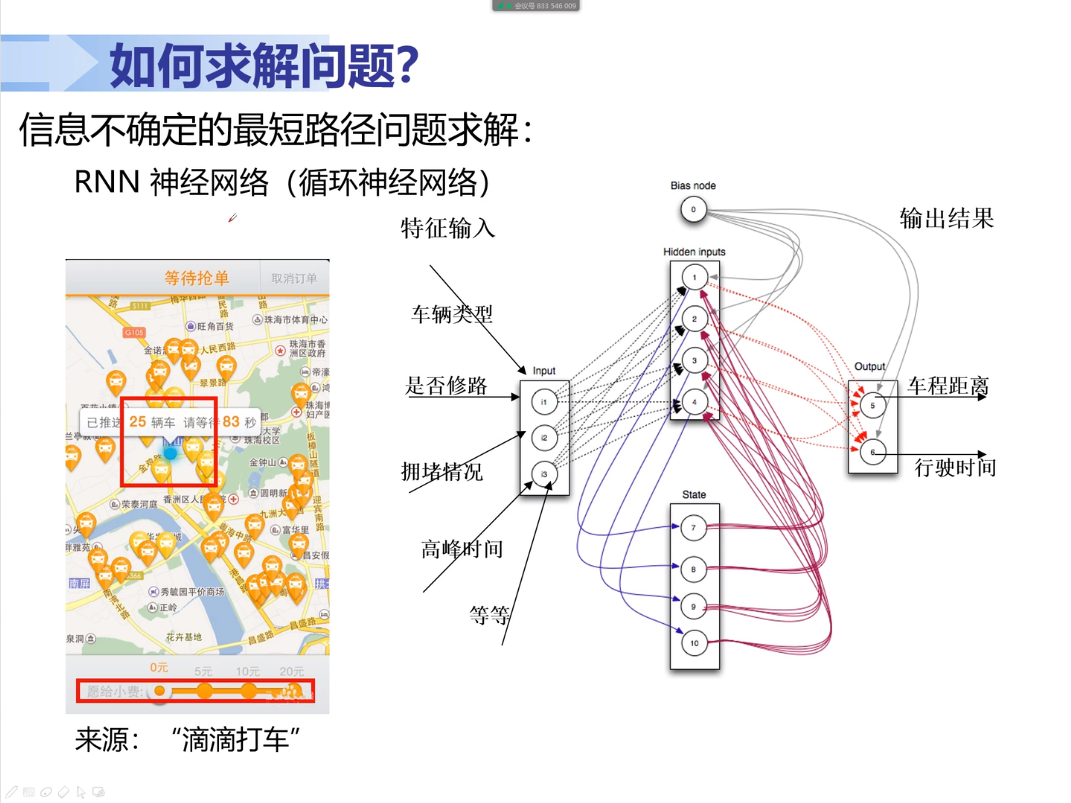
实例:在滴滴打车应用中。早期使用A Star方法进行路径规划和时间估计;在后期取得了更多大数据后,利用这些数据采用RNN(循环神经网络)算法进行路径规划和时间估计。能够比初期的A-Star方法考虑到了更多的复杂因素(例如车辆类型、拥堵、修路、时间、司机驾龄等),所以预估时间更准确。

 京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有
京公网安备 11010802041100号 | 京ICP备19059560号-4 | PHP1.CN 第一PHP社区 版权所有