第五节解析解方式求解模型参数
第四节中我们讲解了最大似然和最小二乘之间的关系&＃xff0c;通过数学原理找到了损失函数为MSE的理论支撑。本节的话我们讲解怎么样基于目标函数为MSE的情况下&＃xff0c;找到最合适的参数模型。在此之前&＃xff0c;我们总结下通过最大似然估计建立目标函数思路&＃xff1a;
1. 建立线性模型&＃xff08;将误差视为未统计到的多个维度影响的结果&＃xff09;
2. 对于误差假设其服从均值为0的高斯分布
3. 得到每个数据点被采样到的概率分布函数&＃xff08;自变量为θ&＃xff09;
4. 最大似然估计--总概率最大
5. 通过两边取ln和公式整理&＃xff0c;得到结论&＃xff1a;mse最小时总似然最大。
我们挨个分析下上面逻辑&＃xff0c;第一条什么是线性模型&＃xff1f;所谓的多元线性回归里面的线性模型就是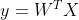
,是一个线性相加的结果&＃xff0c;并且误差视为未统计到的多个维度影响的结果且其服从均值为0的高斯分布。第三条中&＃xff0c;对于每一个样本&＃xff0c;都会得到一个概率分布函数。第四条中&＃xff0c;将所有的样本的概率分布函数累乘&＃xff0c;得到一个似然函数&＃xff0c;我们的目标就是使其总样本发生的概率最大。最后通过对最大似然函数做数学变换&＃xff0c;两边取ln和公式整理&＃xff0c;得到结论为&＃xff1a;mse最小时总似然最大。所以我们得到新的目标&＃xff1a;所谓学习就是 求出一组使mse最小的θ参数。通常&＃xff0c;我们把求一个使某函数达到最大&＃xff08;小&＃xff09;值的自变量解的过程叫做函数最优化&＃xff0c;机器学习实质上都是将参数学习问题转变为函数最优化问题&＃xff0c;进而求解&＃xff0c;所以对于线性回归问题&＃xff0c;我们要做的就是对 
其优化。
那么如何求函数最小值呢&＃xff1f;&＃xff08;函数最优化问题&＃xff09;我们结合高中的知识知道&＃xff0c;直接的思路是求导&＃xff0c;然后使得导数为零的点&＃xff0c;就是我们的最优解。那么这个思想可以应用到求解我们的模型参数吗&＃xff1f;实际上是可以的&＃xff0c;因为都是函数的最优化问题。我们铺垫几个向量求导的预备公式&＃xff1a;
&＃xff1b; 
&＃xff1b; 
&＃xff1b; 
上面我们不用管怎么来的&＃xff0c;就是一些数学公式而已&＃xff0c;有兴趣的自己研究下就可以。先将损失函数写成矩阵形式&＃xff1a;
解释&＃xff1a;因为
是列向量&＃xff08;
是预测的
,减去对应的真实的,所以是一个列向量&＃xff09;&＃xff0c;转置之后
是行向量。所以
根据向量相乘的规则&＃xff0c;对应位置相乘相加&＃xff0c;因为对应位置都是同一个元素&＃xff0c;所以就是右边的
相加&＃xff0c;也就是最终的上面的写成矩阵形式的公式。其中X矩阵是把每个x看做一个行向量张成的矩阵,y是把所有训练集上的y写作一个列向量。
因为我们的目标是想得到一组最小的
&＃xff0c;所以也就是相当于
对求导&＃xff0c;并令其导数为0&＃xff0c;然后解出来&＃xff0c;就是我们的最小的解。既然要求导&＃xff0c;那么我们对目标函数求梯度&＃xff0c;我们说对于向量求梯度&＃xff0c;实际上就是对于向量中的每个参数求导&＃xff0c;这是一 一对应的。我们对目标函数求梯度的过程如下&＃xff1a;
其实上面就是我们根据上面铺垫的向量求导公式结合乘法展开式可得。当梯度为0时&＃xff0c;函数应有极小值。此时
。解得
。称该形式为线性回归目标函数的解析解。因为解析解不是那么重要&＃xff0c;所以不再详细一步步展开上面转换过程。所以我们可以补充总结下线性回归学习的整体流程&＃xff1a;
1. 一开始我们拿到了训练集&＃xff0c;包含若n个数据点,每个点有m个维度&＃xff08;特征&＃xff09;
2. 我们设定线性判别模型 
3. 想要求得最好的一组θ&＃xff08;学习目标&＃xff09;
4. 建立MSE目标函数
5. 对MSE目标函数求使其极小的θ。第一个工具&＃xff1a;解析解。
然而解析解有如下缺陷&＃xff1a;
1. 解析解函数中存在矩阵求逆的步骤&＃xff0c;不是所有矩阵的逆矩阵都可求&＃xff0c;有时候只能求近似解
2. 当数据维度非常高时&＃xff08;几百维度以上&＃xff09; 解析解的求解速度会非常慢&＃xff08;O(n^3))
因此&＃xff1a;通常利用梯度下降法求解函数最小问题的数值解。
所以下一节中&＃xff0c;我们讲解通过梯度下降法求解函数最小问题的数值解&＃xff0c;这个是最常用也是机器学习以后经常见到的&＃xff0c;会对其原理和过程做详细介绍。
京公网安备 11010802041100号