第三节最大似然推导mse损失函数(深度解析最小二乘来源)
在第二节中,我们介绍了高斯分布的来源,以及其概率密度函数对应的参数的解释。本节的话,我们结合高斯分布从数学原理部分解释为什么损失函数是最小二乘。我们再来回归下高斯分布的概率密度函数实际上是这个形式的:

那么这个函数有什么用?其实就是给一个X,就能知道X发生的可能性有多大?相当于给每一个X的一个得分。那么我们回忆一下,在咱们讲这概率论之前,咱们讲的最后一个概念是什么?最小二乘损失函数。我们由什么推到最小二乘?实际上是由误差的概念推导而来,

咱们逐个元素的去分析公式中的含义, 代表第i条数据预测值与真实值之间的差距。
代表第i条数据预测值与真实值之间的差距。 整体是我们的预测值,
整体是我们的预测值, 是我们的真实值。那么预测值中的
是我们的真实值。那么预测值中的 代表什么呢?这里不免讲到一个学科叫做线性代数,我个人的理解,线性代数就是一种简化标记法,比如我要写
代表什么呢?这里不免讲到一个学科叫做线性代数,我个人的理解,线性代数就是一种简化标记法,比如我要写 ,写的很累,很长,因为老写这一长串的东西,于是我们干脆引入一个向量的概念,用W乘以X的转置,就等于上面的这些东西,它就是一种运算的定义。即
,写的很累,很长,因为老写这一长串的东西,于是我们干脆引入一个向量的概念,用W乘以X的转置,就等于上面的这些东西,它就是一种运算的定义。即
 代表第i条数据预测值与真实值之间的差距。
代表第i条数据预测值与真实值之间的差距。 整体是我们的预测值,
整体是我们的预测值, 是我们的真实值。那么预测值中的
是我们的真实值。那么预测值中的 代表什么呢?这里不免讲到一个学科叫做线性代数,我个人的理解,线性代数就是一种简化标记法,比如我要写
代表什么呢?这里不免讲到一个学科叫做线性代数,我个人的理解,线性代数就是一种简化标记法,比如我要写 ,写的很累,很长,因为老写这一长串的东西,于是我们干脆引入一个向量的概念,用W乘以X的转置,就等于上面的这些东西,它就是一种运算的定义。即
,写的很累,很长,因为老写这一长串的东西,于是我们干脆引入一个向量的概念,用W乘以X的转置,就等于上面的这些东西,它就是一种运算的定义。即
怎么解释上面公式?此时的 通常在咱们手写的时候,通常会写成
通常在咱们手写的时候,通常会写成 ,这就是向量的意思。那什么叫向量?假如说我的W向量为
,这就是向量的意思。那什么叫向量?假如说我的W向量为 是什么意思呢?此时
是什么意思呢?此时 不再是一个实数了,而是由三个实数构成的这么一个集合体,你就简单地把它联系理解成三个数的一个组合,把三数放一块,我把三个数硬生生写成一个字母,要不我还得称它
不再是一个实数了,而是由三个实数构成的这么一个集合体,你就简单地把它联系理解成三个数的一个组合,把三数放一块,我把三个数硬生生写成一个字母,要不我还得称它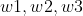 ,好麻烦!,所以我们直接称它叫
,好麻烦!,所以我们直接称它叫 向量,其中它的第一个元素是1,第二个元素是2,第三个元素是3,它们三个整体构成了一个叫做三维向量,因为它是由三个元素构成的。向量为了方便运算,定义了行向量和列向量,横着写的就叫行向量,竖着写的叫列向量。这些东西没有什么原因就这么定义的,就是一个起名。我们把从行向量变成列向量的运算叫做转置,比如
向量,其中它的第一个元素是1,第二个元素是2,第三个元素是3,它们三个整体构成了一个叫做三维向量,因为它是由三个元素构成的。向量为了方便运算,定义了行向量和列向量,横着写的就叫行向量,竖着写的叫列向量。这些东西没有什么原因就这么定义的,就是一个起名。我们把从行向量变成列向量的运算叫做转置,比如 ,它的转置就是竖着写下上面的向量。为什么要转来转去?因为我们定义了行向量乘以列向量这种运算。 我们此时对于这个例子来说,A向量乘以B向量的转置,假设A是行向量
,它的转置就是竖着写下上面的向量。为什么要转来转去?因为我们定义了行向量乘以列向量这种运算。 我们此时对于这个例子来说,A向量乘以B向量的转置,假设A是行向量 ,B是列向量
,B是列向量 的转置
的转置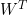 。那么一个行向量乘一个列向量怎么定义?就是行的第一个元素乘以列向量的第一个元素的结果,加上行的第二个元素乘以列向量的第二个元素结果,加上行的第三个元素乘以列向量的第三个元素的结果,就是
。那么一个行向量乘一个列向量怎么定义?就是行的第一个元素乘以列向量的第一个元素的结果,加上行的第二个元素乘以列向量的第二个元素结果,加上行的第三个元素乘以列向量的第三个元素的结果,就是 =
= 。那么
。那么 这个公式就可以借用上面行向量乘以列向量的表示方式。我们通常把
这个公式就可以借用上面行向量乘以列向量的表示方式。我们通常把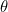 都定义为列向量,那么
都定义为列向量,那么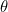 的本身是
的本身是 的一个列向量,
的一个列向量, 就是
就是 的一个行向量。那么
的一个行向量。那么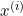 怎么解释?每一条数据x是不是有n个维度,X本身是不是也可以给它写成一个向量?我们就直接写
怎么解释?每一条数据x是不是有n个维度,X本身是不是也可以给它写成一个向量?我们就直接写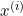 向量就包含了这一条数据的所有维度了,当它为列向量的情况下,
向量就包含了这一条数据的所有维度了,当它为列向量的情况下, 就变成了一个行向量乘以列向量的形式。所以目前为止就把线性代数当作一种运算的简写方式。际上你就把这想成就是一个暗号,你看到这个暗号,你就知道它背后根据向量的乘法的定义会得到一个这样的结果,就是
就变成了一个行向量乘以列向量的形式。所以目前为止就把线性代数当作一种运算的简写方式。际上你就把这想成就是一个暗号,你看到这个暗号,你就知道它背后根据向量的乘法的定义会得到一个这样的结果,就是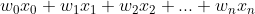 ,也就是
,也就是 这么一个结果,它计算出来的结果是什么?就是我们的
这么一个结果,它计算出来的结果是什么?就是我们的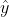 ,也就是我们的预测值。那么
,也就是我们的预测值。那么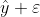 是不是就是我们的真实值?刚好符合我们的公式。
是不是就是我们的真实值?刚好符合我们的公式。
 通常在咱们手写的时候,通常会写成
通常在咱们手写的时候,通常会写成 ,这就是向量的意思。那什么叫向量?假如说我的W向量为
,这就是向量的意思。那什么叫向量?假如说我的W向量为 是什么意思呢?此时
是什么意思呢?此时 不再是一个实数了,而是由三个实数构成的这么一个集合体,你就简单地把它联系理解成三个数的一个组合,把三数放一块,我把三个数硬生生写成一个字母,要不我还得称它
不再是一个实数了,而是由三个实数构成的这么一个集合体,你就简单地把它联系理解成三个数的一个组合,把三数放一块,我把三个数硬生生写成一个字母,要不我还得称它 向量,其中它的第一个元素是1,第二个元素是2,第三个元素是3,它们三个整体构成了一个叫做三维向量,因为它是由三个元素构成的。向量为了方便运算,定义了行向量和列向量,横着写的就叫行向量,竖着写的叫列向量。这些东西没有什么原因就这么定义的,就是一个起名。我们把从行向量变成列向量的运算叫做转置,比如
向量,其中它的第一个元素是1,第二个元素是2,第三个元素是3,它们三个整体构成了一个叫做三维向量,因为它是由三个元素构成的。向量为了方便运算,定义了行向量和列向量,横着写的就叫行向量,竖着写的叫列向量。这些东西没有什么原因就这么定义的,就是一个起名。我们把从行向量变成列向量的运算叫做转置,比如 ,它的转置就是竖着写下上面的向量。为什么要转来转去?因为我们定义了行向量乘以列向量这种运算。 我们此时对于这个例子来说,A向量乘以B向量的转置,假设A是行向量
,它的转置就是竖着写下上面的向量。为什么要转来转去?因为我们定义了行向量乘以列向量这种运算。 我们此时对于这个例子来说,A向量乘以B向量的转置,假设A是行向量 ,B是列向量
,B是列向量 的转置
的转置 这个公式就可以借用上面行向量乘以列向量的表示方式。我们通常把
这个公式就可以借用上面行向量乘以列向量的表示方式。我们通常把 我们总结下上面说的核心。误差是由我们多个未观测到的属性或者叫特征决定的,多个未观测到的属性共同决定误差,我们应该假设它符合同一个高斯分布,什么样的高斯分布呢?就是误查服从一个均值为零,方差虽然你不知道,但一定也是某个确定的值的高斯分布。好,上面的核心你已了解,我们就可以引入一个概率的问题,一个可能性问题。既然误差服从均值为零的高斯分布,那误差自己的概率密度函数写出来如下:
某一个误差发生的概率是不是就应该等于上面的公式。用心观察一下这个式子怎么来的?还记得高斯分布的概率密度函数吗?

对比发现是不是只有 这个公式,所以把样本被采样到的概率中
这个公式,所以把样本被采样到的概率中 替换成
替换成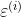 ,结果是一样的,只不过我们要从实际含义去理解。
,结果是一样的,只不过我们要从实际含义去理解。
 这个公式,所以把样本被采样到的概率中
这个公式,所以把样本被采样到的概率中 既然知道每个样本采样到的概率后,那我们来计算这个概率。可以发现这里面真正变得是  ,因为其他参数都是已知,假如
,因为其他参数都是已知,假如 全等于0,你算出来的是一个概率,假如
全等于0,你算出来的是一个概率,假如 全等于1,算出来是另一个概率,也就是说每一条样本被采样到的可能性是随着
全等于1,算出来是另一个概率,也就是说每一条样本被采样到的可能性是随着 的变化而变化的。这是某一条样本被采样到的概率,而最终所有的样本都被你采样到了。比如说你拿到了1万条数据,拿第一条数据,是不是有一组
的变化而变化的。这是某一条样本被采样到的概率,而最终所有的样本都被你采样到了。比如说你拿到了1万条数据,拿第一条数据,是不是有一组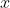 ,有一个
,有一个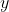 ,分别是
,分别是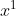 和
和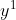 ,带进去上面的概率公式,得到一个关于
,带进去上面的概率公式,得到一个关于 的一个表达式。只要
的一个表达式。只要 确定,结果也就确定了。那么第一条样本被抽样到的概率是一个关于
确定,结果也就确定了。那么第一条样本被抽样到的概率是一个关于 的表达式,第二个样本被抽样到的概率也是一个关于
的表达式,第二个样本被抽样到的概率也是一个关于 的表达式,跟第一个表达式不一样,因为带进去的
的表达式,跟第一个表达式不一样,因为带进去的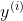 跟
跟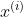 是不一样的,这样下去,你会得到1万个表达式, 每个表达式代表每一个点被抽样到的概率,1万个点共同的被抽样到了,那么你通通把它乘起来,就代表这1万个点共同被你抽样到的概率,得到了一个总的概率。总的概率是高是低取决于谁?
是不一样的,这样下去,你会得到1万个表达式, 每个表达式代表每一个点被抽样到的概率,1万个点共同的被抽样到了,那么你通通把它乘起来,就代表这1万个点共同被你抽样到的概率,得到了一个总的概率。总的概率是高是低取决于谁? 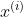 已知
已知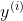 已知,所以总概率高低取决于
已知,所以总概率高低取决于 ,
, 变一变,这总概率就变一变。 那么你希望找到的
变一变,这总概率就变一变。 那么你希望找到的 是使总概率越高还是越低越好?因为你已经抽样到了这些数据,你最合理的
是使总概率越高还是越低越好?因为你已经抽样到了这些数据,你最合理的 应该能让样本总体被抽样到的概率越高越好,
应该能让样本总体被抽样到的概率越高越好, 才越趋近于真实。我们称这种思想叫做极大似然估计(MLE)。所谓似然就是上面说的1万个
才越趋近于真实。我们称这种思想叫做极大似然估计(MLE)。所谓似然就是上面说的1万个 的表达式相乘的结果就叫似然,其实就是最大概率估计,只不过民国时期翻译那些经典的数学书籍的时候,把概率翻译成了似然。
的表达式相乘的结果就叫似然,其实就是最大概率估计,只不过民国时期翻译那些经典的数学书籍的时候,把概率翻译成了似然。
由于训练集上的样本被抽选到这个随机事件是彼此独立的,那么训练集上所有的样本全部都被抽选到的概率转换为数学公式就是:
通常我们称上面的总概率函数为似然函数。那什么样的 是最好的
是最好的 呢?能够使这个式子最大的θ就是最好的
呢?能够使这个式子最大的θ就是最好的 。因为它代表整个训练及被抽样到的总概率,既然它已经发生的事情,概率理应最大,这样
。因为它代表整个训练及被抽样到的总概率,既然它已经发生的事情,概率理应最大,这样 才最真实,否则
才最真实,否则 计算出来,这个概率没有达到最大,说明给的
计算出来,这个概率没有达到最大,说明给的 不够好,毕竟这些东西已经被你抽到了,这个概率还没达到最高值,说明给的
不够好,毕竟这些东西已经被你抽到了,这个概率还没达到最高值,说明给的 不够合理。所以最大似然的思想就是已经抽样到的样本的总概率应该最大,而最合理的
不够合理。所以最大似然的思想就是已经抽样到的样本的总概率应该最大,而最合理的 就应该是让似然函数最大的
就应该是让似然函数最大的 。这一点只要理解透了,后面的东西都很简单,这是本节最大的重点,极大似然估计会出现在机器学习的方方面面。方方面面都会有极大似然估计,它的核心思想就是已经发生的概率理应最大,而且概率取决于谁?取决于
。这一点只要理解透了,后面的东西都很简单,这是本节最大的重点,极大似然估计会出现在机器学习的方方面面。方方面面都会有极大似然估计,它的核心思想就是已经发生的概率理应最大,而且概率取决于谁?取决于 。
。
我们不要忘记初心,我们机器学习,学习的是一组参数 ,其实就是
,其实就是 ,本质就想找到一组最好的
,本质就想找到一组最好的 ,现在似然函数是不是相当于给了我们一个指导方针? 能够让总概率最大(也就是似然函数最大)的
,现在似然函数是不是相当于给了我们一个指导方针? 能够让总概率最大(也就是似然函数最大)的 就是最好的
就是最好的 。
。
那么这跟那MSE函数(损失函数)有什么关系?我们回顾之前的知识,我们的目的是想找到一组一组参数 ,即(
,即( ),使损失函数(MSE)最小,而本节讲的是让这组参数
),使损失函数(MSE)最小,而本节讲的是让这组参数 (即
(即 ),使似然函数最大,那么他们之间矛盾吗?要是能找到他们之间的关系,是不是所有的原理,无论从哪一方面都能解释通了。所以下一节中,我们来解剖MSE和最大似然之间的真正关系。
),使似然函数最大,那么他们之间矛盾吗?要是能找到他们之间的关系,是不是所有的原理,无论从哪一方面都能解释通了。所以下一节中,我们来解剖MSE和最大似然之间的真正关系。











 京公网安备 11010802041100号
京公网安备 11010802041100号