前言:数字滤波器可以用软件或者硬件实际实现,具体采用哪种实现方式取决于其应用,选择在有限精度运算的条件下提供让人满意的性能的实现方法。
1.
系统框图 1.1如何由复杂的系统框图得到系统的传输函数?
令系统输入为X,输出为Y,写出所有加法器的输入输出表达式,联立所有加法器的方程,消项,得到H=Y/X=…。
1.2.无延迟回路
对于数字滤波器结构的物理实现来说,
框图中必须排除无延迟回路----->[z-1]----->
典范结构:
若在框图表示中,延迟的数量等于差分方程的阶数(即传输函数的阶数),则这种数字滤波器结构是典范结构
1.3.等效结构
若两个滤波器有着相同的传输结构,则定义它们的结构是等效的。
有一种相当简单的方法通过转置运算将系统框图转变为等效系统
1)倒转所有路径
2)把节点换成加法器,把加法器换成节点
3)交换输入节点x[n]和输出节点y[n]
2.基本FIR数字滤波器结构
由于FIR滤波器可以设计成在整个频率范围内均可提供精确的线性相位,而且总是可以与滤波器系数保持BIBO稳定无关,因此很多应用中,FIR滤波器是首选。
2.1 直接型
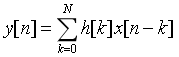
框图:
2.2 级联型
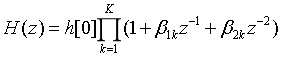
框图:
2.3 线性相位FIR结构
复习:线性相位FIR的冲激响应满足以下性质
h[n]=h[N-n]或h[n]=h[N-n]
以一个对称冲激响应为例:
3.基本IIR数字滤波器结构
3.1 直接型
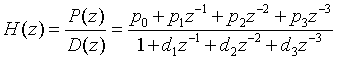
将其分解为两个传输函数H1(z)和H2(z)的级联,其中
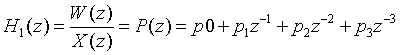

直接型分为Ⅰ型(非典范结构)和Ⅱ型(典范结构)
Ⅰ型:
Ⅱ型:
3.2 并联实现
真分式:分子最高次数大于分母最高次数
假分式:分子最高次数小于分母最高次数
并联实现时,一定要将真分式单独化出一个数,变成假分式再因式分解。
因式分解技巧:
本章难点
1.求H(z)/H(ejω)的幅度|H(z)/H(ejω)|
以H(z)为例,H(ejω)只需令H(z)|z=ejω即可
方法:直接求|H(z)|2=H(z)H(z-1)
2.H(z)因式分解