作者:翔云飘雪9_694_492 | 来源:互联网 | 2023-09-09 12:47
迷人的两度搜索
1、BFS和DFS
深度优先搜索算法(DFS)和广度优先搜索算法(BFS)是一种用于遍历或搜索树或图的算法,在搜索遍历的过程中保证每个节点(顶点)访问一次且仅访问一次,按照节点(顶点)访问顺序的不同分为深度优先和广度优先。
1.1、深度优先搜索算法
深度优先搜索算法(Depth-First-Search,DFS)沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。 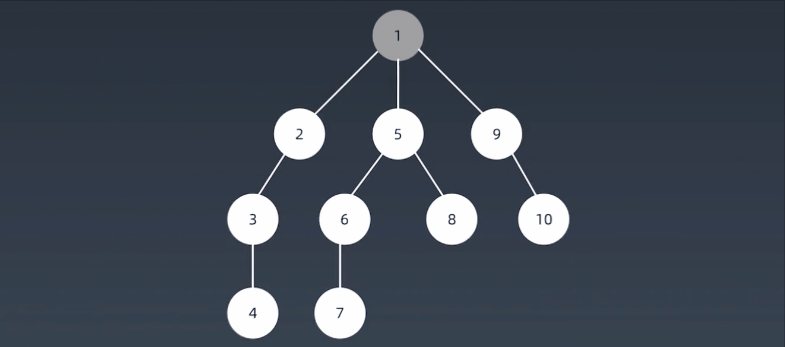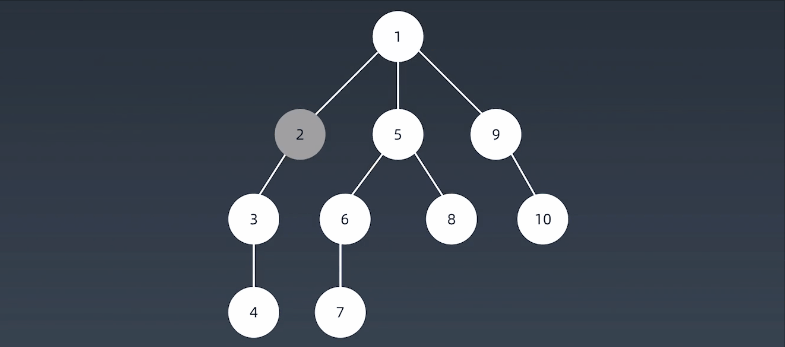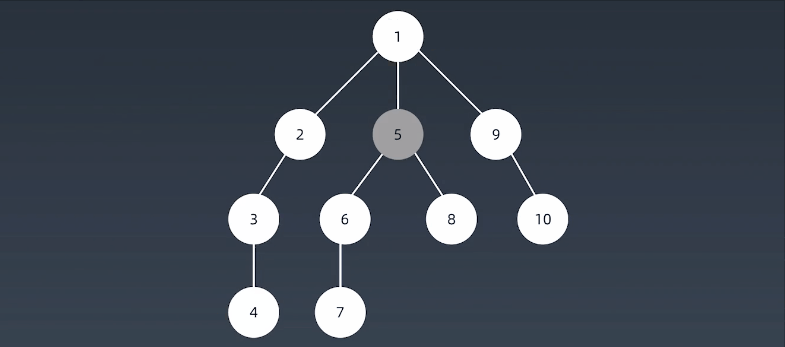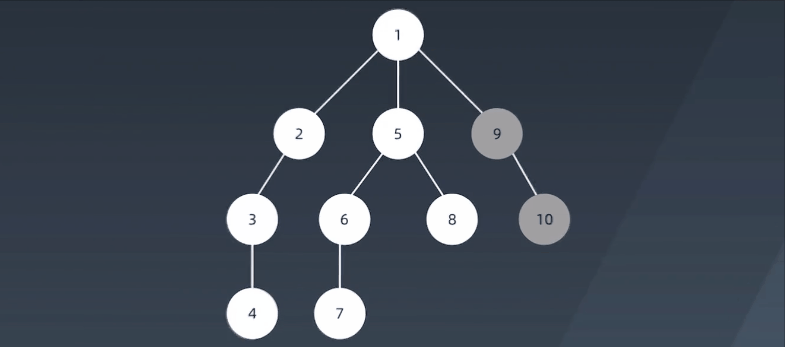
注意:
1:实际上,回溯算法思想就是借助于深度优先搜索来实现的。
DFS负责搜索所有的路径,回溯辅以选择和撤销选择这种思想寻找可能的解,当然代码写起来基于递归(所以代码写起来就是用递归实现的)。
2:DFS跟回溯有什么关系呢?
回溯是一种通用的算法,把问题分步解决,在每一步都试验所有的可能,当发现已经找到一种方式或者目前这种方式不可能是结果的时候,退回上一步继续尝试其他可能(有一个选择和撤销选择的过程,可理解为标记访问和删除访问标记)。很多时候每一步的处理都是一致的,这时候用递归来实现就很自然。
当回溯(递归)用于树(图)的时候,就是深度优先搜索。当然了,几乎所有可以用回溯解决的问题都可以表示为树。(像之前的排列,组合等问题,虽不是直接在树上操作,但是他们操作的中间状态其实是一棵树)那么这俩在这里就几乎同义了。如果一个问题解决的时候显式地使用了树或图,那么我们就叫它dfs。很多时候没有用树我们也管它叫dfs严格地说是不对的,但是dfs比回溯打字的时候好输入。
DFS代码参考模板:
//Java private void dfs(TreeNode root,int level,List> results){ //terminal 已下探到最底部节点 if(results.size()==level){ // or root == null or node alread visited results.add(new ArrayList<>()); return; } // process current level node here. results.get(level).add(root.val); // 记录当前节点已被访问 //drill down if node not visited if(root.left!=null){ dfs(root.left,level+1,results); } if(root.right!=null){ dfs(root.right,level+1,results); } }
是不是觉得跟二叉树的前中后序遍历很像,其实二叉树的前中后序遍历就是一种DFS,只不过记录节点的时机不一样而已。
针对多叉树的DFS,代码参考模板如下:
//Java public void dfs(Node node,List res) { //terminal if (node == null) { return; } //process current level logic res.add(node.val); //drill down List children = node.children; for (Node n:children) { // if node not visited then dfs node if (not visited) { // 在基于图的dfs中一般需要判断顶点是否已访问过 dfs(n,res); } } }
当然我们也可以自己使用栈来模拟递归的过程,将递归代码改写成非递归代码!
针对图的深度优先搜索算法,思路是一致的:
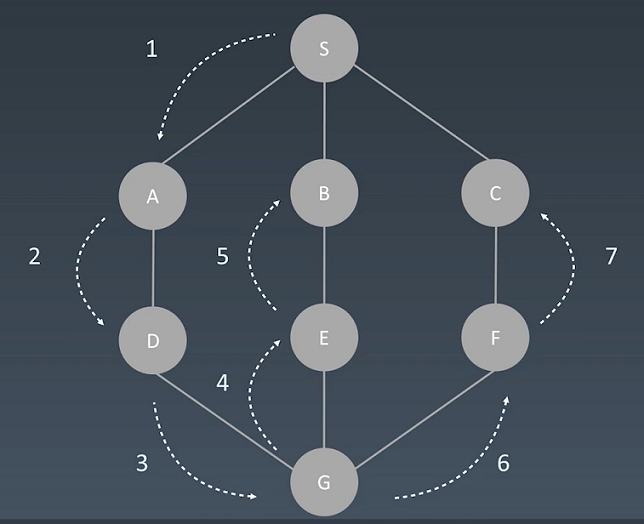
假设:从S开始进行查找,每次查找,先一头扎到底,然后再回退,回退过程中有别的路再一头扎到底。比如:S->A->D->G->E->B,到底了,然后回退到G,再一头扎到底,S->A->D->G->F->C
1.2、广度优先搜索算法
广度优先搜索算法(Breadth-First-Search,BFS)直观地讲,它其实就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。
简单的说,BFS是从根节点开始,沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问,则算法中止,一般用队列数据结构来辅助实现BFS算法。
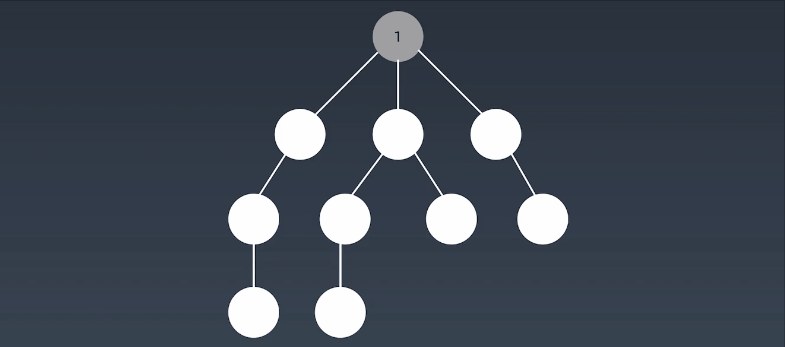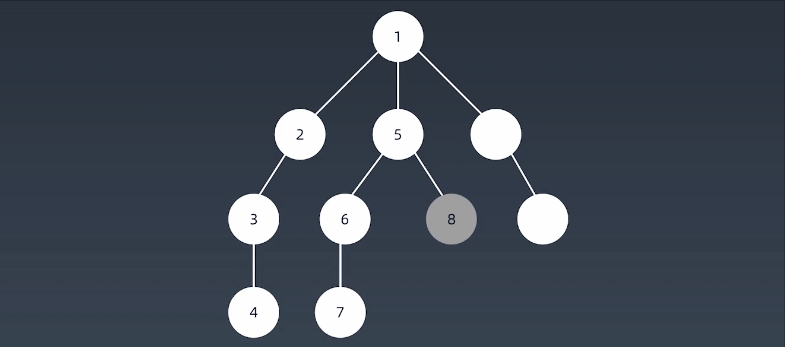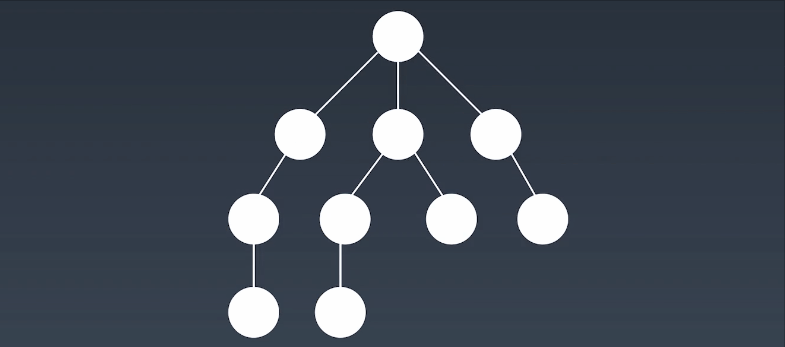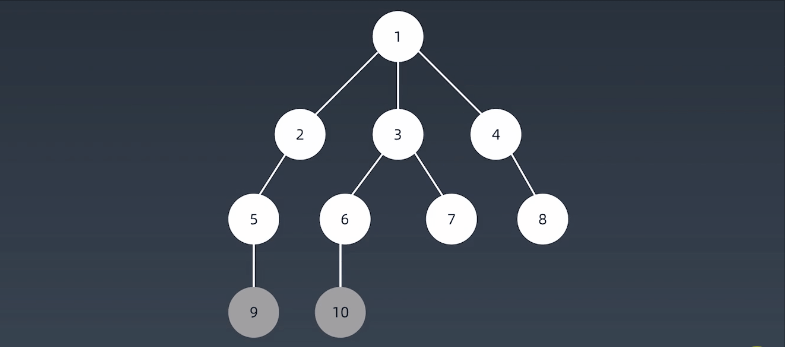
就像在湖面上滴一滴水,形成的水波纹!向四周散开
dfs和bfs搜索方式的比较:
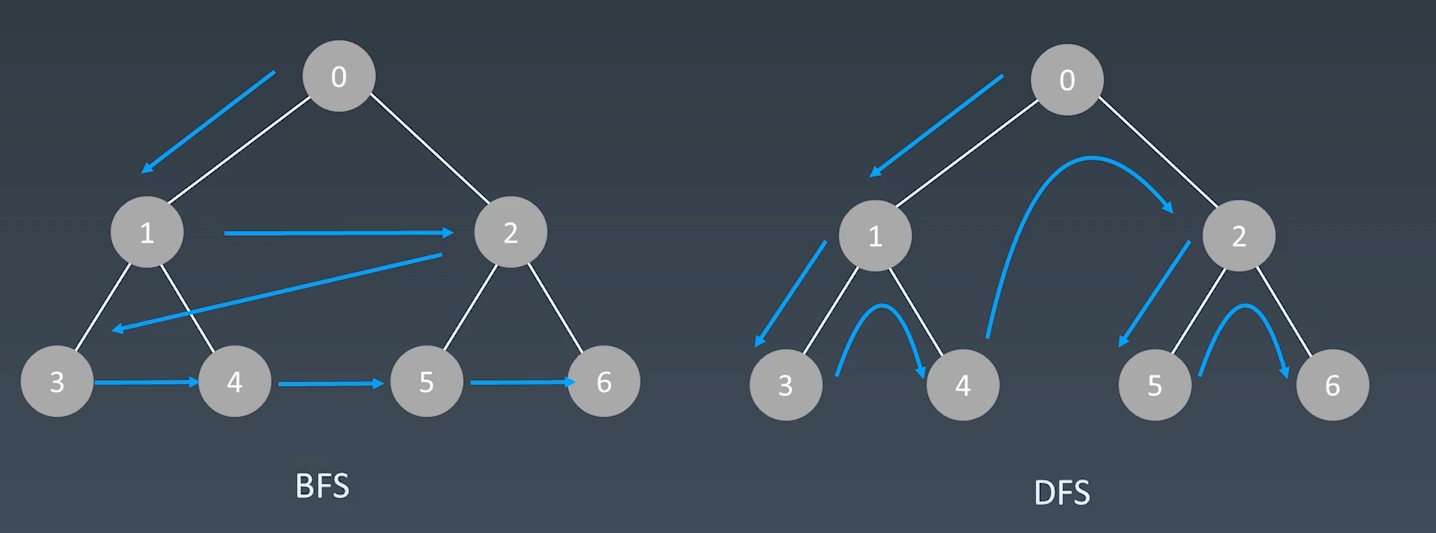
BFS代码的参考模板:需要借助一个队列Queue(或Deque)
//Java public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode(int x) { val = x; } } public List> levelOrder(TreeNode root) { List> allResults = new ArrayList<>(); if (root == null) { return allResults; } Queue nodes = new LinkedList<>(); //将根节点入队列 nodes.add(root); while (!nodes.isEmpty()) { //每次循环开始时:队列中的元素的个数其实就是当前这一层节点的个数 int size = nodes.size(); List results = new ArrayList<>(); for (int i = 0; i
就相当于刚开始把公司老总放入队列,这是第一层,然后把老总的直接下级比如:vp,总监等,取出来,然后放入队列,到了vp,总监这一层时,再把他们的直接下属放入队列。
在图中的广度优先搜索过程如下:
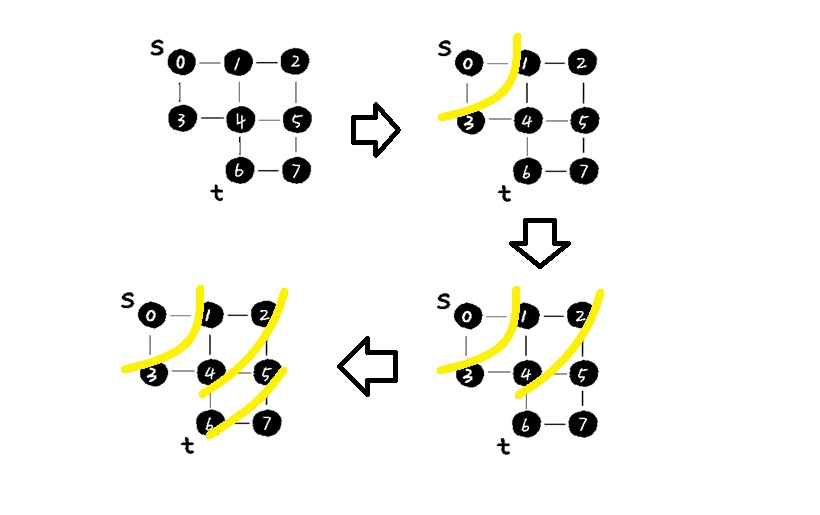
参考该网址上的演示过程:https://visualgo.net/zh/dfsbfs
应用特点:
1:BFS适合在树或图中求解最近,最短等相关问题
2:DFS适合在树或图中求解最远,最深等相关问题
3:实际应用中基于图的应用居多
2、面试实战
102. 二叉树的层序遍历
滴滴,美团点评,腾讯最近面试题,102. 二叉树的层序遍历
典型的BFS,借助队列FIFO特性,
class Solution { public List> levelOrder(TreeNode root) { //特殊判断 if (root == null) { return new ArrayList(); } Queue queue = new LinkedList(); queue.offer(root); List> res = new ArrayList(); while (!queue.isEmpty()) { int size = queue.size(); List list = new ArrayList(); for (int i=0;i
时间复杂度O(n),空间复杂度O(n)
进阶:能否基于DFS完成
思路:按照深度优先遍历,遍历过程中将当前节点的值添加到它所对应的深度的集合中。因此需要一个在dfs过程中代表深度的变量
class Solution { public List> levelOrder(TreeNode root) { List> res = new ArrayList(); dfs(root,0,res); return res; } public void dfs(TreeNode root,int level,List> res) { //terminal if (root==null) { return; } //将当前层的集合初始化好 int size = res.size(); if ( level > size-1) { res.add(new ArrayList()); } //将当前节点加到当前层对应的集合中 List list = res.get(level); list.add(root.val); //drill down dfs(root.left,level+1,res); dfs(root.right,level+1,res); } }
104. 二叉树的最大深度
嘀嘀打车,百度最近面试题,104. 二叉树的最大深度
如果我们知道了左子树和右子树的最大深度 l 和 r,那么该二叉树的最大深度即为
max(l,r)+1
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此使用递归
其实这也是DFS的体现,直接下探到最深处得到最大深度,然后左右两边比较即可。
class Solution { public int maxDepth(TreeNode root) { return dfs(root); } //求一棵子树的最大深度 public int dfs(TreeNode node) { //终止条件 if (node == null) { return 0; } //左子树最大深度 int leftDepth = dfs(node.left); //右子树最大深度 int rightDepth = dfs(node.right); //当前节点的最大深度为左子树最大深度和右子树最大深度中的最大值+1 return Math.max(leftDepth,rightDepth) +1; } }
时间复杂度:O(n),其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次。
空间复杂度:O(height),其中height 表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的深度,因此空间复杂度等价于二叉树的高度。
进阶:能否用BFS完成
利用一个计数器,每遍历完一层就计一个数,直到所有层都遍历结束
class Solution { public int maxDepth(TreeNode root) { //特殊判断 if (root==null) { return 0; } Queue queue = new LinkedList(); queue.add(root); int deep = 0; while (!queue.isEmpty()) { int size = queue.size(); for (int i=0;i
小结:
在实际应用中,DFS要比BFS应用的广泛!
515. 在每个树行中找最大值
facebook,百度,字节面试题,515. 在每个树行中找最大值
典型的BFS
class Solution { public List largestValues(TreeNode root) { List res = new ArrayList(); if (root==null) { return res; } Queue queue = new LinkedList(); queue.offer(root); while (!queue.isEmpty()) { int size = queue.size(); int max = Integer.MIN_VALUE; for (int i=0;i
200. 岛屿数量
亚马逊,华为,字节最近面试题,很高频,200. 岛屿数量
典型的图的搜索,立马想到DFS和BFS
class Solution { //定义顶点向:上下左右,各走一步的方向信息 int[][] directiOns= {{0,1},{0,-1},{-1,0},{1,0}}; //定义网格的行数 int rows; //定义网格的列数 int clos; public int numIslands(char[][] grid) { //定义岛屿总数 int count = 0; //获取网格有多少行 rows = grid.length; if (rows==0) { return count; } //获取网格有多少列 clos = grid[0].length; //定义网格各顶点是否被访问过 boolean[][] visited = new boolean[rows][clos]; //从图中去找能构成岛屿的顶点 for (int i=0;i=0 && x=0 && y
其他题目
127. 单词接龙
529. 扫雷游戏
36. 有效的数独
本文由传智教育博学谷教研团队发布。
如果本文对您有帮助,欢迎关注和点赞;如果您有任何建议也可留言评论或私信,您的支持是我坚持创作的动力。
转载请注明出处!