21.合理的模型初始化和激活函数

以两个变量为例&＃xff0c;均值为零可以让变量于自己的轴对称&＃xff0c;那么在二维上整个变量分布就是中心对称&＃xff0c;而方差则可以控制各个变量离原点的离散程度&＃xff0c;那么就可以把二维变量看成限制在某个圈内。

在梯度计算时&＃xff08;偏导&＃xff09;时&＃xff0c;梯度方向大致是向着圆心的&＃xff0c;那么梯度步长就有一个较大的可调范围&＃xff0c;不会出现z字形的梯度路径。

独立同分布IID(independent and identically distributed)

1. 因为是正态分布随机生成的权重&＃xff0c;因此第t层的权重矩阵的期望&＃xff08;均值&＃xff09;为0&＃xff0c;而方差等于某个初始化的数。
2. 对于第t层来说&＃xff0c;这一层的输入和这一层的权重是相互独立的
3. 最后一点我的理解如下&＃xff1a;

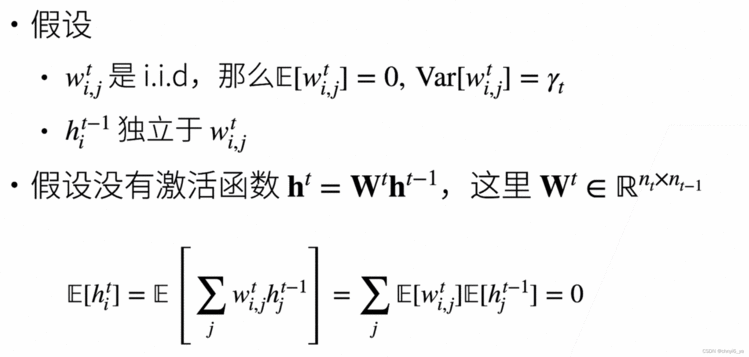
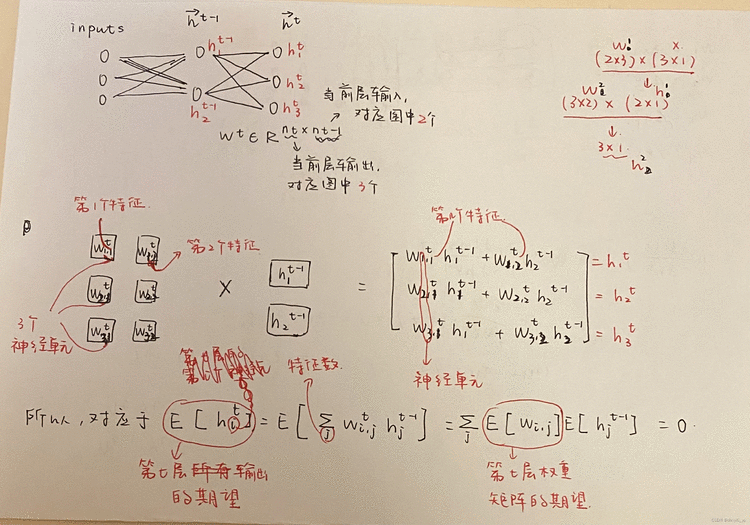
ps&＃xff1a; 当X和Y相互独立时&＃xff0c;E&＃xff08;XY&＃xff09;&＃61;E&＃xff08;X&＃xff09;E&＃xff08;Y&＃xff09;&＃xff0c;第一项是0&＃xff0c;以及之前假设了第二项是0&＃xff0c;最后相乘结果为0

正向方差

方差D&＃xff08;x&＃xff09; &＃61; E&＃xff08;X^2 &＃xff09;- E&＃xff08;X&＃xff09; ^ 2

反向方差和均值

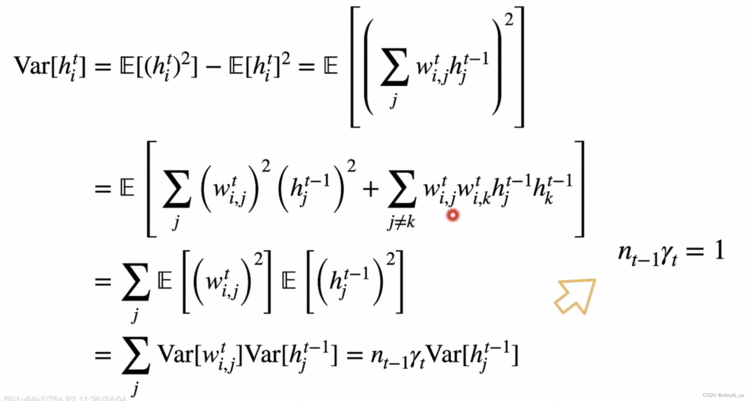
注意&＃xff1a;第一行t-1和t弄反了。

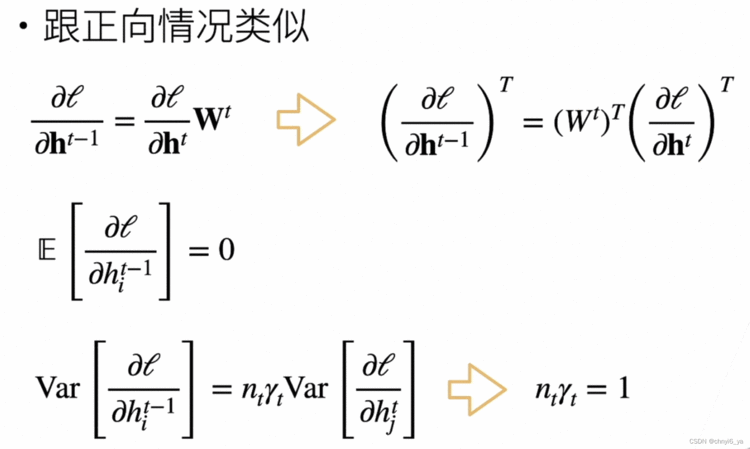
最后的结果可知&＃xff0c;第t层的输出的个数乘以γ要等于1.

nt-1 * γt &＃61; 1保证前项的输出的方差是一致的&＃xff0c;nt * γt &＃61; 1保证梯度是一样的。

但是nt-1是第t层输入的维度&＃xff0c;nt是第t层输出的维度&＃xff0c;除非输入的维度和输出的维度一样&＃xff0c;不然的话无法同时满足两个条件。

均匀分布 var&＃xff08;x&＃xff09; &＃61; 1 / 12&＃xff08;a-b&＃xff09;^2

权重初始化时的方差是根据输入和输出维度来定的。

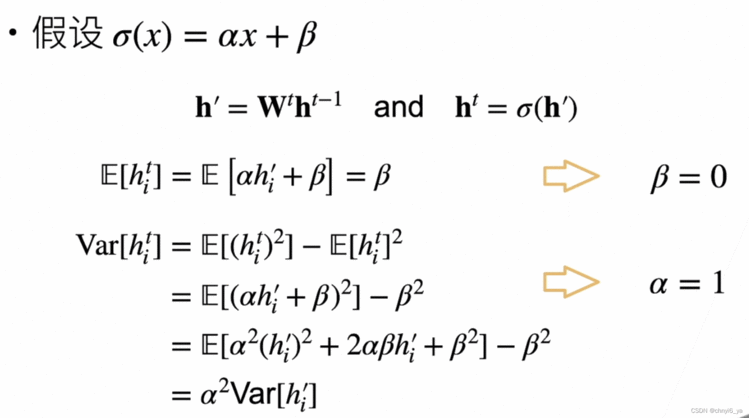
关于期望和方差的公式

反向

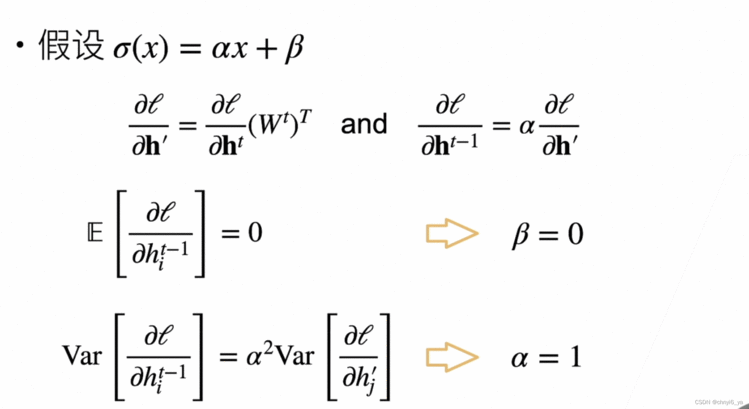
如果希望每一层输出以及梯度的均值为0&＃xff0c;方差为固定数的话&＃xff0c;只有激活函数f&＃xff08;x&＃xff09;&＃61;x满足条件。

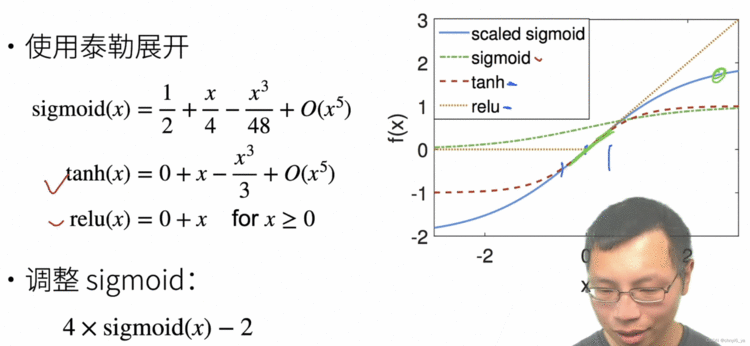
可以看出&＃xff1a;tanh&＃xff0c;relu以及调整后的sigmoid都可以选取。

• 合理的权重初始值和激活函数的选取可以提升数值稳定性。

1. 出现nan&＃xff0c;inf的情况以及怎么解决&＃xff1f;
   答&＃xff1a;inf 是学习率调得太大了&＃xff0c;或者权重初始的值太大了&＃xff0c;导致梯度爆炸&＃xff0c;nan一般是除以0&＃xff0c;梯度已经很小了&＃xff0c;梯度除以了0&＃xff0c;就会得到nan。

解决&＃xff1a;1&＃xff09;合理的初始化权重 2&＃xff09;选择正确的激活函数 3&＃xff09;学习率不要选太大。实际碰到了的话&＃xff0c;就把学习率一直往小调整&＃xff0c;知道nan或inf不出现。也可以看权重的初始&＃xff0c;让方差的区间小一点&＃xff0c;一直往小走&＃xff0c;使得出现值&＃xff0c;再慢慢调大使得训练有进展

2. 在训练的过程中&＃xff0c;如果网络层的输出的中间层特征元素的值突然变成nan了&＃xff0c;是发生了梯度爆炸了吗&＃xff1f;
   答&＃xff1a;是的&＃xff0c;nan一般就是梯度太大造成的&＃xff0c;梯度太小的话&＃xff0c;是训练不动的&＃xff0c;没有进展。

3. sigmoid能引起梯度消失&＃xff0c;但是别的情况也会导致梯度消失&＃xff0c;用relu代替sigmoid有一定的概率解决梯度消失&＃xff0c;但不一定。

4. 通过把每一层输出的均值和方差做限制&＃xff0c;可以理解为限制各层输出值出现极大或极小的异常值。