基于遗传算法的MATLAB入门与应用指南

引言

遗传算法是模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法。

遗传算法能有效的求解NP（非确定行多项式）问题以及非线性、多峰函数优化和多目标优化问题。

其本质是一种并行、高效、全局搜索的方法，它能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应的控制搜索过程以求得最优解。

遗传算法的生物学基础

达尔文的生存斗争中适者生存、不适者淘汰的自然选择过程，遗传与变异是决定生物计划的内在因素。遗传能使生物的性状不断的传送给后代，变异能够使生物的性状发生改变，从而适应新的环境而不断地向前发展。

遗传物质的主要载体是染色体，基因是有遗传效应的片段，存储着遗传信息，可以准确的复制，也能够发生突变。生物体通过对基因的复制和交叉，使其性状的遗传得到选择和控制。同时，通过基因重组、基因变异、和染色体在结构和数目上的变异产生丰富多彩的变异现象。

生物遗传与进化的规律有：

1. 生物的所有遗传信息都包含在其染色体中，染色体决定了生物的性状。染色体是由基因及其有规律的排列构成。


2. 生物的繁殖过程是由其基因的复制过程来完成的。同源染色体的交叉或变异会产生新的物种，使生物呈现新的性状。


3. 对环境适应能力强的基因或染色体比适应能力差的基因或然的题更有机会遗传到下一代。

遗传算法理论基础

模式定理

模式：描述种群中在位串的某些确定位置上具有相似性的位串自己的相似性模板（一串字符）。

模式阶定义：模式H中确定位置的个数。

定义距定义：在模式H中第一个确定位置和最后一个确定位置之间的距离称为该模式的定义距。

模式定理：在遗传算法选择、交叉和变异算子的作用下，具有低阶、短定义距，并且其平均适应度高于群体平均适应度的模式在子代中将呈指数级增长。

积木块假设

积木块定义：具有低阶、短定义距，并且高平均适应度的模式成为积木块。

积木块假设：个体的积木块通过选择、交叉、变异等遗传算子的作用，能够相互结合在一起，形成高阶、长距、高平均适应度的个体编码串。

遗传算法的基本概念

变异 变异操作

遗传算法的流程

1. 初始化种群。获得每个个体的二进制编码。

   
   



2. 计算适应度。将每个个体的二进制编码转化为指定范围内的十进制数，通过适应度函数（目标函数）计算每个个体的适应度。

   
   



3. 选择操作。使用轮盘赌的选择方法进行选择。

   轮盘赌选择：又称比例选择方法．其基本思想是：各个个体被选中的概率与其适应度大小成正比．具体操作如下：

   (1)计算出群体中每个个体的适应度f(i=1，2，…，M)，M为群体大小；

   (2)计算出每个个体被遗传到下一代群体中的概率；

   

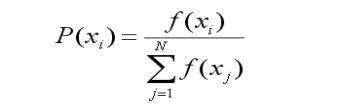
   (3)计算出每个个体的累积概率；

   

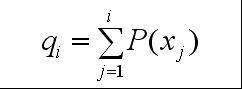
   （q[i]称为染色体x[i] (i=1, 2, …, n)的积累概率）

   

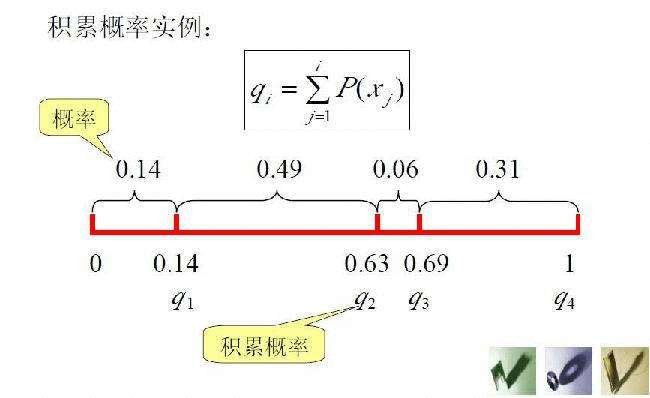
   (4)在[0，1]区间内产生一个均匀分布的伪随机数r；

   (5)若r

   (6)重复(4)、(5)共M次。

   
   



4. 交叉操作

   (1)从交配池中随机取出要交配的一对个体。

   (2)根据位串长度L，对要交配的一对个体随机选取[1,L-1]中的一个或多个整数K作为交叉位置。

   (3)根据交叉概率Pc实施交叉操作，配对个体在交叉位置处相互交换各自的部分基因，从而形成一对新个体。

   
   



5. 变异操作

   （1）对种群中所有个体按事先设定的变异概率判断是否进行变异。

   （2）对进行变异的个体随机选择变异位进行变异。

   
   



6. 终止条件判断：达到迭代次数最大值。

   
   

一个简单例子：

求函数f(x) = x+10sin(5x)+7cos(4x)的最大值，其中x的取值范围为[1,10].`

%用遗传算法求函数f(x) = x+10sin(5x)+7cos(4x)的最大值，其中x的取值范围为[1,10].
close all;
clc;
NP = 50; %种群个体数
L = 20; %二进制编码长度，即染色体长度
Pc = 0.8; %交叉概率
Pm = 0.1; %变异概率
G = 100; %迭代代数
Xs = 10; %区间最大值
Xx = 0; %区间最小值
f = randi([0,1],NP,L); %初始化种群
%%%%%%%%%%%%%遗传算法循环%%%%%%%%%%%%%
for k = 1:G %迭代过程%%%%%%%将二进制解码为定义域范围内十进制%%%%%%%%%%%for i = 1:NPU = f(i,:);m = 0;for j = 1:Lm = U(j)*2^(j-1)+m; endx(i) = Xx + m * (Xs-Xx) /(2^L-1);Fit(i) = func1(x(i));end%%%%%%%适应度归一化%%%%%%%%%maxFit = max(Fit); %最大适应度值minFit = min(Fit); %最小适应度值rr = find(Fit == maxFit);fBest = f(rr(1,1),:); %保存最大适应度值xBest = x(rr(1,1)); %保存最大适应度位置Fit = (Fit - minFit) / (maxFit - minFit);%%%%%%%基于轮盘赌的复制选择操作%%%%%%%%%%sum_Fit = sum(Fit);fitvalue = Fit ./ sum_Fit; %计算每个适应度值的概率fitvalue = cumsum(fitvalue); %计算累计概率ms = sort(rand(NP,1)); %NP次赌盘的旋转newi = 1;fiti = 1;while newi <= NPif ms(newi) end
xBest;
figure;
plot(trace)
xlabel('迭代次数')
ylabel('目标函数值')
title('适应度进化曲线')
%%%%%%%%%%%适应度函数%%%%%%%%%%%%
function result = func1(x)
fit = x + 10*sin(5*x) + 7*cos(4*x);
result = fit;
end